17.1 Binary Codes

1. Use the circle diagram method shown in Figures 17.1 and 17.2 (page 700) to verify the code words in Table 17.1 (page 702) for the messages 0101, 1011, and 1111.

2. Use the circle diagram method to decode the received messages 0111011 and 1000101.

3. Find the distance between each of the following pairs of words:

4. Referring to Table 17.1, use the nearest-neighbor method to decode the received words 0000110 and 1110100.

5. If the code word 0110010 is received as 1001101, how is it decoded using the circle diagram method?

6. Suppose that a received word has the circle diagram arrangement shown here:

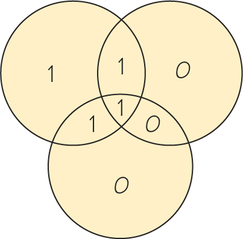
What can we conclude about the received word?

7. Suppose that a received word has the circle diagram arrangement shown here:

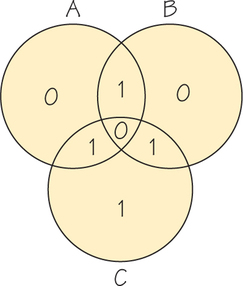
Assuming that exactly one error was made in transmission, what was the sent word?

8. If the code word 1010 in the code $C_2$ in Example 4 (page 706) is received as 1000, explain why the error will be detected but cannot be corrected.

9. For the code $C_4$ in Example 4, decode the following received messages:

10. If the code word 0010111 in the code C₄ in Example 4 is received as 1010110, will the error be detected? Can it be corrected?

17.2 Encoding with Parity-Check Sums

11. Determine the binary linear code that consists of all possible three-digit messages with three check digits appended using the parity-check sums $a_2+a_3,a_1+a_3$ and $a_1+a_2$. (That is, $c_1=0$ if $a_2+a_3$ is even, $c_1=1$ if $a_2+a_3$ is odd, and similarly for $c_2$ and $c_3$.)

12. Let $C$ be the code

{0000000, 0010111, 0101011, 1001101, 1100110, 1011010, 0111100, 1110001}

What is the error-correcting capability of $C$? What is the error-detecting capability of $C$?

13. Find all code words for binary messages of length 4 by appending three check digits using the parity-check sums $a_2+a_3+a_4,a_2+a_4$, and $a_1+a_2+a_3$. Will this code correct any single error?

14. Consider the binary linear code

Use nearest-neighbor decoding to decode 101100 and 101011. If a received word is 001100, can you determine the intended code word? Explain your reasoning.

15. Construct a binary linear code using all eight possible binary messages of length 3 and appending three check digits using the parity-check sums $a_1+a_2$, $a_2+a_3$ and $a_1+a_3$. Decode each of the received words below by the nearest-neighbor method:

001001, 011000, 000110, 100001

16. Extend the code words listed in Table 17.1 (page 702) to eight digits by appending a 0 to words of even weight and a 1 to words of odd weight. What are the error-detecting and error-correcting capabilities of the new code?

17. Extend the code words listed in Table 17.2 (page 704) to eight digits by appending a 0 to words of even weight and a 1 to words of odd weight. What are the error-detecting and error-correcting capabilities of the new code?

18. Suppose that the weight of a binary linear code is 6. How many errors can the code correct? How many errors can the code detect?

19. How many code words are there in a binary linear code that has all possible messages of length 5 with three check digits appended? How many possible received words are there with this code?

17.3 Data Compression

20. Suppose we code a four-symbol genetic set {$A$, $C$, $T$, $G$} into binary form as follows:

Convert the sequence $ACAAGTAAC$ into binary code.

21. Use the code in Exercise 20 to determine the sequence of symbols represented by the binary code 001100001111000.

22. Suppose that we code a five-symbol set {$A$, $B$, $C$, $D$, $E$} into binary form as follows:

Convert the sequence of $AEAADBAABCB$ into binary code. Determine the sequence of symbols represented by the binary code 01000110100011111110.

23. Use the code in Exercise 22 to convert the sequence $EABAADABB$ into binary code. Determine the sequence of letters represented by the binary code 001000110011110111010.

24. Devise a variable-length binary coding scheme for a six-symbol set {$A$, $B$, $C$, $D$, $E$, $F$}. Assume that $A$ is the most frequently occurring symbol, $B$ is the second most frequently occurring symbol, and so on.

25. Judging from the frequency table in Figure 17.9 (page 709), what are the three most frequently occurring consonants in English text material? What is the most frequently occurring vowel?

26. Explain why Morse code must include a space after each letter, but fixed-length codes do not.

27. Following are the closing values (rounded to the nearest integer) of the Dow Jones Industrial Average stock market values for a two-week period. Use the delta function method to compress these values. What percentage reduction in characters is there?

28. The following numbers were encoded using delta function encoding. Determine the original numbers.

29. Assume that a dataset of four letters occurs with the following probabilities:

Use a Huffman tree to create a Huffman code for $A$, $B$, $C$, and $D$.

30. Given that the delta function was used to create values in the following list

recreate the original list.

31. Decode the binary string

$11100100001001110110011010$

which has been encoded using the Huffman code given on page 713.

32. Use a Huffman tree to assign a binary code to the letters that occur with the following probabilities:

17.4 Cryptography

33. Use hand computations to calculate the following.

34. Solve for $x$ by trial and error.

35. Use the Caesar cipher to encrypt the message RETREAT. Decrypt the message DGYDQFH, which was encrypted using the Caesar cipher.

36. Suppose a message encrypted with a Caesar shift can be decoded with the same shift. What is the shift?

37. Using $0,1,2,\dots ,25$ to label the positions of the letters $A,B,C,\dots ,Z$, suppose that we create a cipher by replacing the letter in position $i$ with the letter in position $(i+8)mod26$. How many iterations of this cipher must be done before a message will return to its original state?

38. The message ADDAOS was encrypted using the decimation cipher with the key 7. Decrypt it.

39. Explain why 2 cannot be used as the key in a decimation cipher.

40. If you attempted to use the decimation cipher with the key 13, how would the word MESSAGE be encrypted?

41. Use the decimation cipher with the key 5 to encrypt RETREAT.

42. Suppose you wanted to break a code that employed a linear cipher by trying all possible linear ciphers. How many would you have to test to try every one?

43. Find a formula for a linear cipher that decrypts messages encrypted using the formula $11x+20$.

44. List all possible permutations of 1, 2, 3, including 1,2, 3 itself, in a systematic way. (The original ordering 1,2, 3 is viewed as a permutation to simplify various theoretical arguments.)

45. Encrypt the message ADVANCE WHEN READY using the permutation $\alpha =\left[\begin{array}{llll}1\hfill & 2\hfill & 3\hfill & 4\hfill \\ 2\hfill & 4\hfill & 1\hfill & 3\hfill \end{array}\right]$.

46. Encrypt the message ATTACK POSTPONED using the permutation $\alpha =\left[\begin{array}{lllll}1\hfill & 2\hfill & 3\hfill & 4\hfill & 5\hfill \\ 2\hfill & 1\hfill & 5\hfill & 3\hfill & 4\hfill \end{array}\right]$.

47. The message EMTENAOTXOQN was encrypted using the permutation $\alpha =\left[\begin{array}{llll}1\hfill & 2\hfill & 3\hfill & 4\hfill \\ 2\hfill & 4\hfill & 1\hfill & 3\hfill \end{array}\right]$. Decrypt it.

48. The message TAACTPKSTOOPEDN was decrypted using the permutation $\alpha =\left[\begin{array}{lllll}1\hfill & 2\hfill & 3\hfill & 4\hfill & 5\hfill \\ 2\hfill & 1\hfill & 5\hfill & 3\hfill & 4\hfill \end{array}\right]$. Decrypt it.

49. How many permutations of 1, 2, 3, 4 are possible, including the original ordering 1, 2, 3, 4?

50. Use the Playfair cipher with the keyword IMAGINE to encrypt the plaintext CALL ME.

51. The ciphertext WR VI SE CW RY was encrypted with the Playfair cipher using the key WORLD WAR II. Decipher it.

52. Explain why the ciphertext BT TZ PM UO AW AC HK EU W cannot have been encoded using the Playfair cipher.

53. How many possible keys are there for a Jefferson wheel with six disks?

54. Referring to the Jefferson wheel with six disks and the key shown in Example 20 (page 725), what would the encrypted message be if we used the row that is just above the row ATTACK?

55. Referring to the Jefferson wheel with six disks and the key shown in Example 20, what row was used to create the encrypted message MCEMPL?

56. Referring to the Jefferson wheel with six disks shown in Example 20 and the key 5, 1, 4, 2, 6, 3, encrypt the message DEPLOY, using the row directly below the message.

57. Given that BEATLES was used as the keyword for the Vigenère cipher to encrypt SSLETRY TXOGPW, decrypt the message.

58. Use the Vigenère cipher with the keyword CLUE to encrypt the message THE WALRUS WAS PAUL.

59. Use the Vigenère cipher with the keyword HELP to encrypt the message PHONE HOME.

60. Use the linear cipher method with $k=5$ and $s=4$ to encrypt GOOD.

61. Given that the received message ZVW was encrypted using the linear cipher method with $k=11$ and $s=9$, decrypt the message.

62. Add the following pairs of binary strings.

63. For any two binary strings $u$ and $v$ of the same length, define $u+v$ to be the string obtained by summing the strings as explained in Example 21 (page 726). Find $u+v$ for each of the following cases.

64. Suppose that $u$ and $v$ are two binary words of length 7 whose distance apart is 7. What string is $u+v$?

65. Given the binary word $u=1010110$, find all binary words of length 7 that are a distance of 1 from $u$.

66. Suppose that $u$ and $v$ are binary code words of the same length. Using the method of summing binary strings as shown in Example 21, explain why the distance from $u$ to $v$ is the same as the weight of $u+v$.

67. Suppose that $u$, $v$, and $w$ are binary code words of the same length. Using the method of summing binary strings as shown in Example 21, explain why the distance from $u$ to $v$ is the same as the distance from $u+w$ to $v+w$.

68. All binary linear codes have the property that the sum of two code words is another code word. Use this fact to determine which of the following sets cannot be a binary linear code.

Chapter Review

69. Messages encrypted with the __________ cipher are the hardest to break.

70. Explain why for any choice of the key $k$ shown in Table 17.4 (page 717) the number 13 is always encrypted as 13.

71. Suppose a Huffman tree has been used to create a binary code for the letters $A$ through $J$, and the results include $B=111110$, $J=111111$, and $G=11110$. If the code has only two code words of length 6 and one of length 5, what can you say about the probability of the occurrence of the letters $B$, $J$, and $G$?

72. What is the minimum weight of a binary code that can correct any 3 or fewer errors?

73. Explain why encoding ID numbers by multiplying them by 15 would not detect the single-digit error of replacing 1328 by 1326.

74. Explain why any error involving the code word 001 in the code $C_1$ in Example 4 (page 706) is not detected.