19.3 19.2 Rosette and Strip Patterns
The spiral distribution of the seeds in a sunflower head and the spiraling of leaves around a plant stem are instances of similarity and repetition, two key aspects of symmetry.
They also illustrate balance, which refers to regularity in how the repetitions are arranged. In considering patterns with repetition, we distinguish the individual element or figure of the design (the motif) from the pattern of the design —how the copies of the motif are arranged. See, for example, Figure 19.7, which shows two fundamentally different ways of arranging stars.

We explore and classify the fundamentally different ways in which a flat design can be symmetrical. The ideas that we discuss were used by scientists to discover what crystalline forms are possible. Although there is a limitless number of chemical structures, and of motifs that people can make, what is quite surprising is that there is only a limited number of ways to arrange atoms in a structure, or motifs in a design, in a symmetrical way.
How can we identify all the ways that designs can be put together without counting the designs themselves? The key mathematical idea is to look at what you can do to the pattern without changing its appearance.
Rigid Motions
Mathematicians describe various kinds of symmetry by using the geometric notion of a rigid motion, also known as an isometry (which means “same size”). A transformation or “motion” of the plane is a mapping of the entire plane into itself. A rigid motion preserves the distances between every pair of points. You can imagine picking up the plane and moving it as a whole, perhaps rotating it, possibly flipping it over—but without changing its size or shape. For example, moving every point 1 unit in the same direction constitutes a rigid motion.
Rigid Motion DEFINITION
A rigid motion is a transformation of the entire plane that preserves the size and shape of figures. In particular, any pair of points is the same distance apart after the transformation as before.
Figure 19.8 shows the results of how various motions affect the rectangle and its interior in Figure 19.8a. In Figure 19.8b, each side is shrunk by 50%—which is not a rigid motion because the size of the rectangle changes.
For Figure 19.8c, we shear (“squash”) the rectangle; again, this is not a rigid motion because the shape of the rectangle changes. In Figure 19.8d, we rotate the plane 90° (a quarter-turn) counterclockwise around the center of the rectangle: This is a rigid motion. Similarly, in Figure 19.8e, rotating the plane by 180° (a half-turn) is a rigid motion.
In Figure 19.8f, we reflect the rectangle along a vertical mirror down the middle. The right and left halves exchange places.
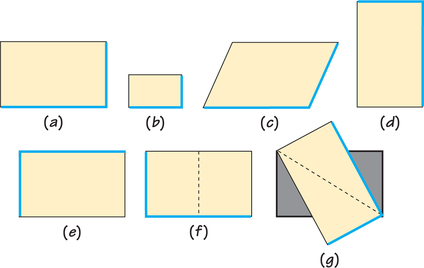
Figure 19.8g shows the result of reflecting across a diagonal of the rectangle. All reflections and all rotations are rigid motions. So are all translations, which move every point in the plane a certain distance in the same direction.
The only remaining kind of rigid motion of the plane is a combination of reflection and translation. Glide reflection is the kind of pattern that your footprints make as you walk: Each successive element of the design (footprint) is a reflection of the previous one (Figure 19.9). The motion combines translation (glide) with a reflection across a line parallel to the direction of the translation.
Glide Reflection DEFINITION
A glide reflection is a translation (=glide) combined with alternating reflection in a line parallel to the translation direction.

Any rigid motion of the plane must be one of the following:
- Reflection (across a line)
- Rotation (around a point)
- Translation (in a particular direction)
- Glide reflection (across a line)
Performing one rigid motion after another results in a rigid motion that (surprisingly) must be one of the four types that we have just explored.
Preserving the Pattern
In terms of symmetry, we are especially interested in rigid motions like those of Figures 19.8e and 19.8f that preserve the pattern— that is, motions for which the pattern looks exactly the same, with all the parts appearing in the same relative places, after the motion is applied.
You might enjoy thinking of applying these motions as “The Pattern Game": You turn your back, I apply a transformation, and then you turn back and see if you can tell whether anything is changed.
The 90° rotation of Figure 19.8a into Figure 19.8d does not preserve the pattern. The moved rectangle doesn’t fit exactly over the original rectangle. On the other hand, the 180° rotation in Figure 19.8e does preserve the pattern. It’s true that the top of the original rectangle is now on the bottom of the transformed version, but you can’t tell. A rotation by any multiple of 180° also would preserve the pattern.
Similarly, the reflection across the vertical line in Figure 19.8f preserves the pattern, while the one in Figure 19.8g, along a diagonal, does not. Spotlight 19.7 discusses possible biological consequences of reflection symmetry or imperfections in it.
“Strive Then to Be Perfect” 19.7
19.7
Is there no such thing as objective and universal beauty, as claimed by American feminist Naomi Wolf in her book The Beauty Myth?
Stand in front of a mirror and look at yourself. Do your left and right sides look exactly symmetrical? What about the part in your hair, freckles on your face, evenness of your shoulders, bending of your ears?
Symmetry may be a proxy for fitness. Symmetrical racehorses tend to run faster; male lions with lopsided facial whisker-spot patterns die younger. The more symmetrical a flower is, the more nectar it produces, making it a better food source for pollinating insects; and correspondingly, insects prefer symmetrical flowers, giving such flowers a better chance of being pollinated.
Perhaps because of association with fitness, symmetry may affect mate selection among animals. Female zebra finches prefer males with symmetrical leg bands. Fruit flies and female barn swallows prefer males with symmetrical tails; a particular parasite can lead to an uneven tail.
What about people? Both male and female Britons, as well as Tanzanian hunter-gatherers, find facial symmetry more attractive than asymmetry.
Perfectly symmetrical female faces that are computer-generated from composites of individual photos appear more attractive to men than photos of actual women’s faces.

The pattern of footsteps in Figure 19.9a is not preserved under reflection along the direction of walking; there is not a left footprint directly across from a right footprint. The pattern is preserved under a glide reflection along the direction of walking, as well as by a translation of two steps, or of four steps, and so on—but not by a translation of one step.
The rigid motions that preserve a pattern are the symmetries of the pattern.
You may think of a pattern as a recipe for repeating a figure (motif) indefinitely. Of course, any pattern in nature or art has only a finite number of copies of the figure. If the recipe for repetition is clear, we can imagine that we are looking at just a part of a pattern that extends indefinitely.
Patterns in the plane can be divided into those that have indefinitely many repetitions in one of the following ways:
- No direction—the rosette patterns
- Exactly one direction (and its reverse)—the strip patterns (sometimes called band patterns or frieze patterns)
- More than one direction (and their reverses)—the wallpaper patterns
Rosette Patterns
A rosette is an ornament or badge made to resemble a flower, and the term rosette pattern is used to describe the possible symmetries of such an ornament or a single flower. The repetition aspect of symmetry consists of the repetition of the petals around the stem. Translations and glide reflections do not come into play. The pattern is preserved under a rotation by certain angles corresponding to the number of petals. There may or may not be reflections that preserve the pattern, depending on whether the petal itself has reflection symmetry. Most flowers do (Figure 19.10a), but some do not.

An everyday example of the rosette pattern—a human-made one—that does not have reflection symmetry is a pinwheel (Figure 19.10b). If there is no reflection symmetry, the motif of the pattern (the element that is repeated) is an entire petal. If there is reflection symmetry, the motif is just half a petal because the entire pattern can be generated by rotation and reflection of a half petal. The fact that these are the only possibilities is sometimes called Leonardo’s theorem, after Leonardo da Vinci, who, in the course of planning the design of churches, needed to decide if chapels and niches could be added without destroying the symmetry of the central design.
Leonardo realized that there are two different classes of rosettes: those without reflection symmetry (cyclic rosettes) and those with it (dihedral rosettes) (see Figure 19.10). The respective notations for the patterns are cn, where the c stands for “cyclic,” and dn, where the d stands for “dihedral,” while n is the number of times that the rosette coincides with its original position in one complete turn around the center. A cyclic pattern has no lines of reflection symmetry, while the dihedral pattern dn has n different lines of reflection symmetry. The flower in Figure 19.10a with its 21 petals (a Fibonacci number!) has dihedral pattern d21 (if we idealize it) because each petal has reflection symmetry, while the pinwheel in Figure 19.10b has pattern c7.
Strip Patterns
We illustrate the different kinds of strip patterns, and their “ingredient” symmetries, with patterns in the art of the Bakuba people of the Democratic Republic of the Congo, who are noted for their fascination with pattern and symmetry (see Spotlight 19.8).
All the strip patterns offer repetition and translation symmetry along the direction of the strip. For simplicity, we position patterns horizontally. For example, in Figure 19.11b, what you can imagine as eyes and a nose (if you rotate the page clockwise) is constantly shifted (translated) along the pattern by the same amount each time.
The pattern may have no other rigid motions that preserve it apart from translation, as in Figure 19.11a.
The other simplest rigid motion to check is reflection symmetry across a line. For a strip pattern, the horizontal center line of the strip may be a reflection line, as in Figure 19.11b; we say that the pattern has symmetry across a horizontal line. There may instead be reflection across a vertical axis, such as the vertical lines through or between the Vs in Figure 19.11c.
Patterns Created by the Bakuba People 19.8
19.8
Among the Bakuba people of the Democratic Republic of the Congo (see the shaded area of the map), it is considered an achievement to invent a new pattern, and every Bakuba king had to create a new pattern at the outset of his reign. The pattern was displayed on the king’s drum throughout his reign and, for some kings, on his dynastic statue.
When missionaries first showed a motorcycle to a Bakuba king in the 1920s, he showed little interest in it. But the king was so enthralled by the novel pattern the tire tracks made in the sand that he had the pattern copied and gave it his name.


Source: Adapted from Jan Vansina, The Children of Woot, University of Wisconsin Press, Madison, 1978, p. 221.
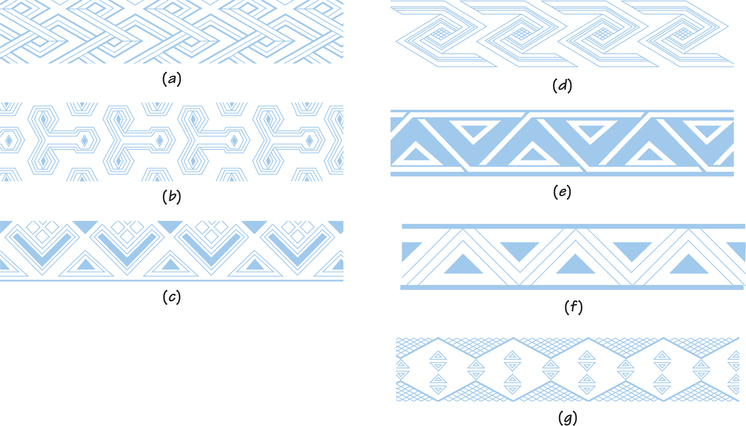
What kind of rotational symmetry can a strip pattern have? The only possibility for a strip pattern is a rotation by 180° (a half-turn), because any other angle won’t even bring the strip back into itself. [We don’t count rotations of 360° or integer multiples of 360° (full turns), because any pattern is preserved under these.] Figure 19.11d shows a strip pattern that is unchanged by a 180° rotation about any point at the center of the small crosshatched regions.
What about glide reflections? A row of alternating p’s and b’s has glide reflection, as shown in the illustration below, in which the dotted line through the middle of the pattern is the line in which reflection takes place.
Glide:pppppppppGlide reflection:pbpbpbpbp
For glide reflection, a p is translated as far as the next b and is then reflected upside down. Figure 19.11e shows a Bakuba pattern whose only symmetry (except for translation) is glide reflection.
Self Check 3
What symmetries—translations, reflections, glide reflections, half-turns—does the pattern of Figure 19.11f have?
- Translations, vertical reflections, half-turns, and glide reflections
Having examined symmetries on strip patterns, we can ask: What combinations of the four are possible? It turns out that apart from the five kinds of patterns we have already seen, there are only two other possibilities: We can have the combination of vertical line reflection together with half-turns and glide reflection, either with horizontal line reflection (Figure 19.11g) or without (Figure 19.11f).
Mathematical analysis reveals the following.
There Are Only Seven Strip Patterns RULE
There are only seven ways to repeat a pattern along a strip.
That this number is so small is quite surprising because there are myriad different design elements (motifs). Two designs may look entirely different, yet share the same pattern of reproducing their design elements.
Wallpaper Patterns and Crystal Structures
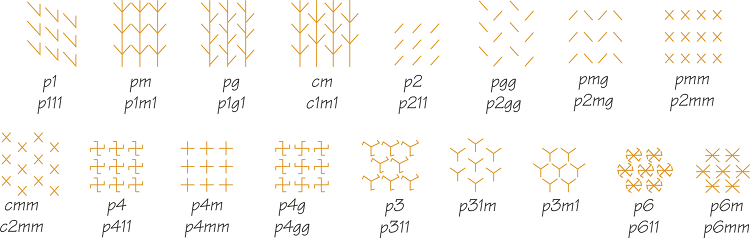
So far, we have classified the patterns that have no translation repetition (the rosette patterns) and those with repetition in one direction (the strip patterns). What about repetitions in more than one direction—say, in two different directions across a plane? It turns out that there are exactly 17 ways to do so, called wallpaper patterns. We give illustrations, notation, and a flowchart later, in Spotlight 19.9.
We emphasize again that “pattern” does not refer to the basic design but to how its repetition is structured across the plane. There is an infinite variety of possible designs that artists can devise. You should imagine that the artist has created one copy of the design and is contemplating how to place equal-sized copies of it in other parts of the (infinite) plane, in a way that is symmetrical. There are very few—just 17—strategies for doing so.
Crystallographers (physicists and chemists interested in the ways that crystals can occur or be built) in the 19th century classified three-dimensional crystal structures in terms of combinations of symmetry elements. They proved—after several years of coming up with different totals!—that there are exactly 230 patterns for crystals. Mathematicians have refined the classification of patterns further to take into account colors that are repeated in a symmetrical way.
The 17 Wallpaper Patterns 19.9
19.9
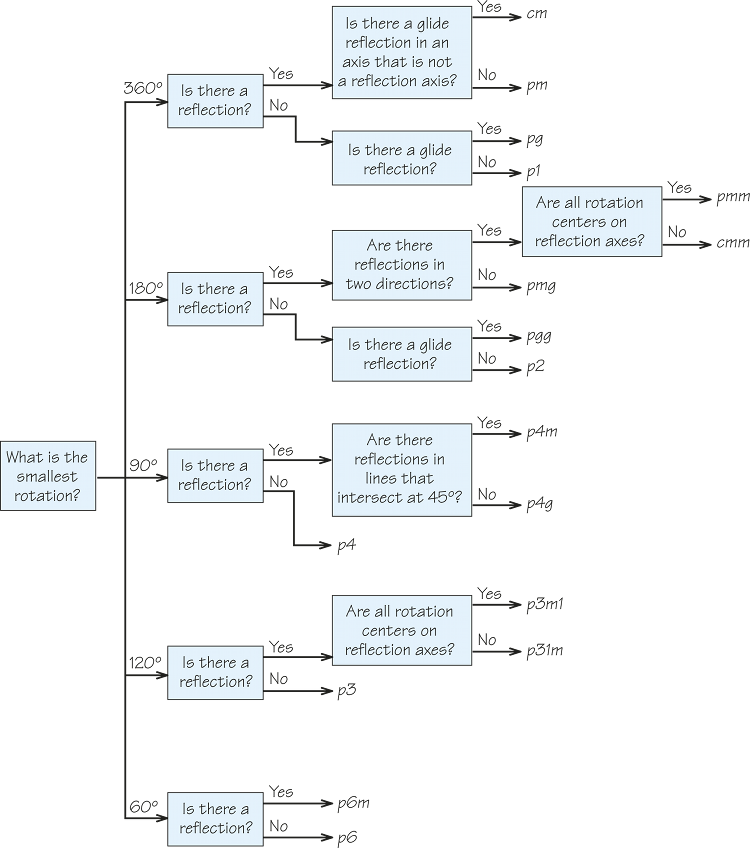
We give an example of each of the 17 wallpaper patterns, together with a flowchart for identifying them. Crystallographers have standard notations and abbreviations for the patterns. The full notation consists of four symbols:
- The first symbol is c (for “centered”) if all rotation centers lie on the reflection lines, or p (for “primitive”) otherwise.
- The second symbol indicates rotational symmetry. It is either 1, 2, 3, 4, or 6, corresponding to the rotational symmetry of, respectively, 360°, 180°, 120°, 90°, and 60°. The symbol is the largest applicable number. For example, if symmetries of 360°, 120°, and 60° are present, the symbol is 6.
- The third symbol is either m, g, or 1, corresponding to the presence of “mirror,” “glide,” or no reflection symmetry.
- The fourth symbol (m, g, or 1) is for describing symmetry relative to an axis at an angle to the symmetry axis of the third symbol.
(Note: The patterns p31m and p3m1 are exceptions to this scheme.)
Below each pattern illustration, we give both the standard abbreviation (on top) and the full notation (below).