19.4 19.3 Notation for Patterns
A standard notation for patterns allows easy communication of which pattern you are seeing. Crystallographic notation is commonly used. For the strip patterns, it consists of four symbols (an example is pma2):
- The first symbol is always a p, which indicates that the pattern repeats (is “periodic”) in the horizontal direction.
- The second symbol is m if there is a vertical line of reflection. Otherwise, it is 1.
The third symbol is
- m (for “mirror”), if there is a horizontal line of reflection (in which case, there is also glide reflection)
- a (for “alternating”), if there is a glide reflection but no horizontal reflection
- 1, if there is no horizontal reflection or glide reflection
- The fourth symbol is 2, if there is half-turn rotational symmetry; otherwise, it is 1.
A 1 always means that the pattern does not have the symmetry corresponding to that position. Figure 19.12 shows the notation schematically.

EXAMPLE 1 Bakuba Patterns
Bakuba Patterns
We use the flowchart of Figure 19.13 to analyze some of the Bakuba patterns of Figure 19.11.
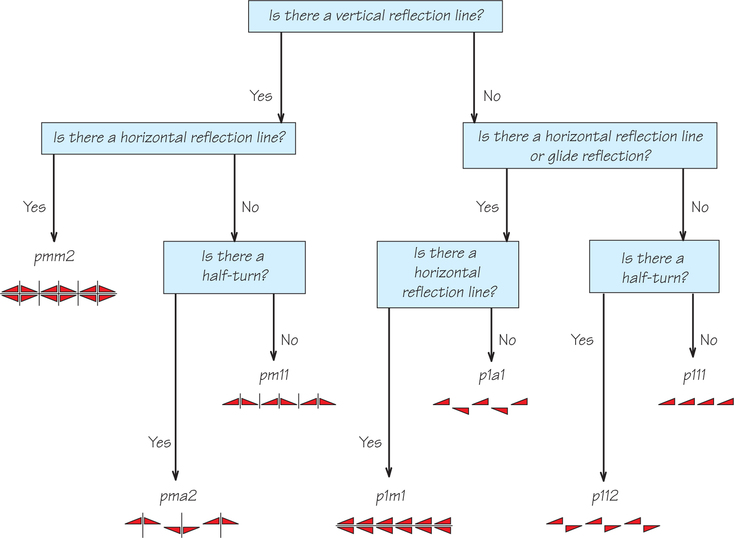
Figure 19.11a does not have a vertical reflection, so we branch right, and the pattern notation begins to take shape as p1__ __. The figure has neither a horizontal reflection nor a glide reflection, so we branch right again, filling in the third position in the notation to get p11_. A half-turn preserves part of but not all the pattern, so we conclude that we have a p111 pattern.
Figure 19.11b does not have vertical reflection, so we branch right to p1_ _. The figure does have horizontal reflection, so we branch left and left, concluding that the pattern is p1m1.
Figure 19.11f has vertical reflection, so we branch left to pm_ _. The figure does not have horizontal reflection, so we branch right but cannot yet fill in the third symbol. The figure does have a half-turn symmetry (and glide symmetry), with its center on the middle of the three lines between any pair of closest triangles. So the pattern is pma2.
Self Check 4
What is the pattern notation for the pattern in Figure 19.11c?
- pm11
Remember the Bakuba people’s fascination with tire treadmarks? Apart from aesthetic value, certain symmetries are important for practical purposes. The Museum of Transport in Glasgow, Scotland, includes all kinds of vehicle tires. However, only five of the seven strip patterns appear among treads of all the tires there. Examining Figure 19.13, can you guess which two patterns do not appear, what they have in common, and the practical reason why they are not used in tire treads?
Imperfect Patterns
In applying these classification schemes to patterns on real objects, we need to take into account that the pattern may not be perfectly rendered. Also, patterns not on flat surfaces—for example, the pattern around the rim of a bowl or around the body of a jar—require some latitude in interpretation.
EXAMPLE 2 Patterns on Pueblo Pottery
Patterns on Pueblo Pottery
The pitchers in Figures 19.14abc are from thousand-year-old Pueblo sites in what is now the Southwestern United States. Consider the patterns on the bodies of the pots, which continue on the back sides. Let’s suppose that they could be unwrapped and continued as strip patterns, but we’ll disregard the patterns on the handles.
What are the patterns on the pots? We immediately come up against the question of the perfectness of the patterns. In Figure 19.14c, the rendering of the jagged pattern near the top of the pitcher is done rather crudely, and the pattern lower down is not done much better. Is this lack of pattern? It hardly seems so—more likely, there was just a lack of perfection in executing a pattern in the mind of the potmaker. Generosity compels us to opt for this latter interpretation for our analysis.
Similarly, in Figure 19.14d, if we regard the pot as having a single pattern going around the pot, we notice that the top part of the pattern is not matched exactly to the bottom part. Also, it’s not clear if the vertical line in the middle of the pot face is supposed to be part of the pattern, or whether it is also reproduced on the unseen part. To be strict, we would decide at least that there are two separate patterns (upper and lower) separated by a white-line edge. But there also appears to be an attempted match-up between the two parts (however inexactly done) that we may not want to deny. We could attribute the variations (including the vertical line) to artistic license and consider the pot as having a single pattern around it.
We follow the flowchart in Figure 19.13 on page 799 and get the following results:
- Figure 19.14a: Is there a vertical reflection? No. Is there a horizontal reflection or glide reflection? No. Is there a half-turn? No. Hence, the pattern is p111. In fact, it looks a lot like the example at far right in Figure 19.13.
- Figure 19.14b: Is there a vertical reflection? No. Is there a horizontal reflection or glide reflection? No. Is there a half-turn? Yes. The pattern is p112. (The “jags” may represent zigzagging lightning bolts.)
- Figure 19.14c (top band): Is there a vertical reflection? No (notice the little “teeth” on the lower left and upper right edges only). Is there a horizontal reflection? No. Is there a half-turn? Yes. The pattern is p112.
- Figure 19.14c (lower band): Is there a vertical reflection? No. Is there a horizontal reflection? No. Is there a half-turn? Yes. This pattern too is p112.
- Figure 19.14d (lower band only): Is there a vertical reflection? Yes. Is there a horizontal reflection? Yes. The pattern is pmm2.

Women made the pots in the Pueblo culture, and they strongly preferred the symmetry of half-turns. Very few of their pots have any reflection symmetry, neither mirror or glide reflection. The avoidance of reflection symmetry was a consistent feature of ancient pottery of the indigenous peoples of the Western Hemisphere.
The pot in Figure 19.14d, as you might then surmise, is much more recent.
Self Check 5
What is the notation for the pattern of Figure 19.11f on page 795?
- pma2