1.4 1.3 Beyond Euler Circuits
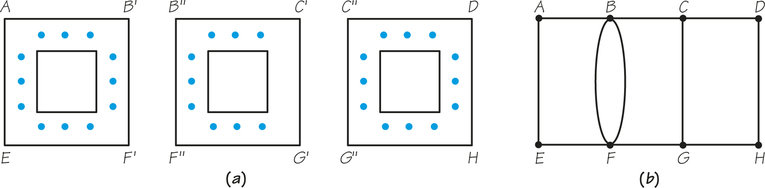
Now let’s see what Euler’s theorem tells us about the three-block neighborhood with parking meters, represented by dots in Figure 1.12a. Figure 1.12b shows the corresponding graph. (Because we use edges to represent only sidewalks along which the officer must walk, the sidewalk with no meters is not represented by any edge in the graph.) This graph has vertices with odd valences (at vertices C and G), so Euler’s theorem tells us that there is no Euler circuit for this graph.
Because we must reuse some edges in this graph to cover all edges in a circuit, for efficiency we need to keep the total length of reused edges to a minimum. Note that we are still looking for a tour that starts and ends at the same vertex. This type of problem, in which we want to minimize the length of a circuit by carefully choosing which edges to retrace, is often called the Chinese postman problem. (Like parking-control routes, mail routes need to be efficient.) The problem was first studied by the Chinese mathematician Meigu Guan in 1962—hence the name. The remainder of this chapter is dedicated to solving the Chinese postman problem and discussing applications beyond parking control.
Solving the Chinese Postman Problem
In a realistic Chinese postman problem, we need to consider the lengths of the sidewalks, streets, or whatever “costs” the edges have (represent) because we want to minimize the total length of the reused edges. However, to simplify things at the start, we can suppose that all edges represent the same length. (This is often called the simplified Chinese postman problem.) In this case, we need only count reused edges and need not add up their lengths. To solve the problem, we want to find a circuit that covers each edge and that has the minimal number of reuses of edges already covered.
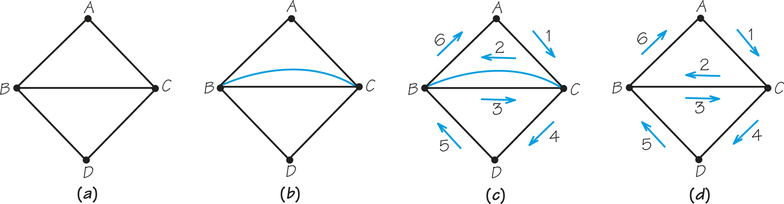
To follow the procedure we are going to develop, look at the graph in Figure 1.13a, which is essentially the same graph as in Figure 1.12b. This graph has no Euler circuit, but there is a circuit that has only one reuse of an edge (CG), namely, ABCDHGCGFBFEA. Let’s draw this circuit so that when edge CG is about to be reused, we install a new, extra, blue edge in the graph for the circuit to use. By duplicating edge CG, we can avoid reusing the edge. To duplicate an edge, we must add an edge that joins the two vertices that are already joined by the edge we want to duplicate. (It makes no sense to join vertices that are not already connected by an edge, because such edges would not represent sidewalk sections with meters; see Figure 1.15.)
We have now created the graph of Figure 1.13b. In the graphs we draw, the edges that are added will be shown in color to distinguish them from the original edges, which are shown in black. (In the graphs that you draw, you may want to use a similar scheme, perhaps dotted edges, to help you remember which edges are the originals and which are duplicated.) In the graph of Figure 1.13b, the original circuit can be traced as an Euler circuit, using the new edge when needed. The circuit is shown in Figure 1.13c. Our theory will be based on using this idea in reverse, as follows:
- Take the given graph and add edges by duplicating existing edges, until you arrive at a graph that is connected and even-valent. Note that after a graph is eulerized, the new graph produced will have an Euler circuit.
- Find an Euler circuit on the eulerized graph.
- “Squeeze” this Euler circuit from the eulerized graph onto the original graph by reusing an edge of the original graph each time the circuit on the eulerized graph uses an added edge.
Eulerizing a Graph DEFINITION
Adding edges that duplicate existing edges to a connected graph to make all valences even is called eulerizing the graph.
EXAMPLE 3 Eulerizing a Graph
Eulerizing a Graph
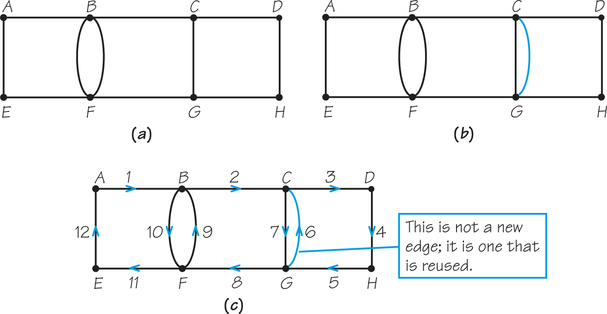
Suppose we want to eulerize the graph of Figure 1.14a. When we eulerize a graph, we first locate the vertices with odd valence. The graph in Figure 1.14a has two, B and C. Next, we add one end of an edge at each such vertex, matching up the new edge with an existing edge in the original graph. Figure 1.14b shows one way to eulerize the graph. Note that B and C have even valence in the second graph. After eulerization, each vertex has even valence. To see an Euler circuit on the eulerized graph in Figure 1.14c, simply follow the edges in numerical order and in the direction of the arrows, beginning and ending at vertex A. The final step, shown in Figure 1.14d, is to “squeeze” our Euler circuit onto the original graph. There are two reuses of previously covered edges. Notice that each reuse of an edge corresponds to an added edge.
In the previous example, we noticed that we could count how many reuses we needed by counting added edges. This is generally true in this type of problem: If you add the new edges correctly, the number of reuses of edges equals the number of edges added during eulerization.
Adding new edges correctly means adding only edges that are duplicates of existing edges. Doing this makes the rule just stated in italics always true, and so it is easy to count the needed reuses.
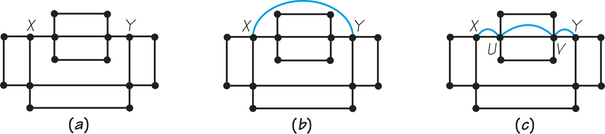
To see why we add only duplicate edges, examine Figure 1.15a. We need to alter the valences of vertices X and Y by adding edges so that they become evenvalent. Adding one long edge from X to Y (Figure 1.15b) might seem like an attractive idea, but adding this edge is equivalent to asking a snowplow, say, to get from X to Y without moving along existing streets. At times it is necessary to traverse sections of the graph that have been previously traversed. This is the significance of the duplicated edges. Here the structure of the graph forces us to repeat some edges. We cannot get away with fewer than three repeats: the three edges XU, UV, and VY (Figure 1.15c). The duplicated edges are shown in color.
Now that we have learned to eulerize, the next step is to try to get a best eulerization—one with the fewest added edges. It turns out that often there are many ways to eulerize a graph. It is even possible that the smallest number of added edges can be achieved with two different eulerizations. This is the reason we use the phrase “a best eulerization” rather than “the best eulerization.” Remember, we want a best eulerization because this enables us to find the circuit for the original graph that has the minimum number of reuses of edges, which in typical applications means saving time or money by avoiding retraversing edges where the productive work has already been accomplished (avoiding deadheading).
EXAMPLE 4 A Better Eulerization
A Better Eulerization
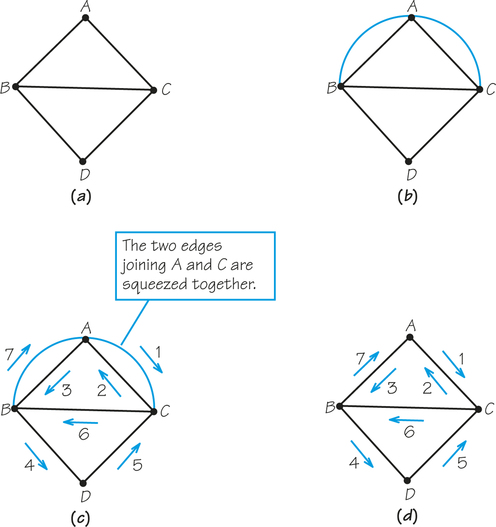
In Figure 1.16a, we begin with the same graph as in Figure 1.14, but we eulerize it in a different way—by adding only one edge (see Figure 1.16b). Figure 1.16c shows an Euler circuit on the eulerized graph, and in Figure 1.14d we see how it is squeezed onto the original graph. There is only one reuse of an edge, because we added one edge during eulerization.
The solution in Figure 1.16 is better than the solution in Figure 1.14 because one reuse is better than two. These examples suggest the following addition to our solution procedure: Try to find an eulerization with the smallest number of added edges. This extra requirement makes the problem both more interesting and more difficult. For large graphs, a best eulerization may not be obvious. We can try out a few and pick the best among the ones we find, but there may be an even better one that our haphazard search does not turn up.
A systematic procedure for finding a best eulerization does exist, but the process is complicated. There is a particularly easy technique for eulerizing a special category of networks often found in residential neighborhoods. A street network is called rectangular when composed of a series of rectangular blocks that form a large rectangle a certain number of blocks high and a certain number of blocks wide.
Examples of rectangular street networks (a 3-by-3, a 3-by-4, and a 4-by-4) are shown in Figure 1.17. The graph on the right in each pair shows a best eulerization for the rectangular street network on the left. There appear to be three different eulerization patterns, depending upon whether the rectangle height and width in the original graph are odd or even numbers. In Figure 1.17a, both lengths are 3, both odd; in Figure 1.17b, one length is odd (3) and one is even (4); in Figure 1.17c, both lengths are 4, an even number.
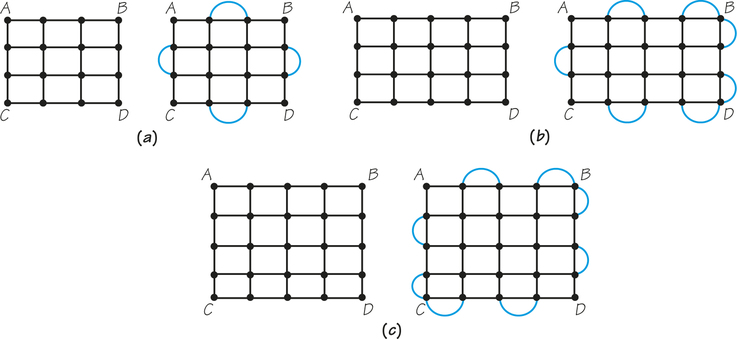
Although the patterns appear different, one technique can be used to create all of them. This technique can be thought of as involving an “edge walker” who walks around the outer boundary of the large rectangle in some direction, say, clockwise. He starts at any corner, say, the upper-left corner. As he goes around, he adds edges by the following rules. When he comes to an odd-valent vertex, he links it to the next vertex with an added edge. This next vertex now becomes either even or odd. If it became even, he skips it and continues around, looking for an odd vertex. If it became odd (this could happen only at a corner of the big rectangle), the edge walker links it to the next vertex and then checks this vertex to see whether it is even or odd. Each of the three parts of Figure 1.17 has been eulerized by this method.
In a street network that is not rectangular, the eulerization process is started by locating all the vertices with odd valence and then pairing these vertices with each other and finding the length of the shortest path between each pair. We look for the shortest paths because each edge on the connecting paths will be duplicated. The idea is to choose the pairings cleverly so that the sum of the lengths of those paths is the smallest it can be. With a little practice, most people can find a best or nearly best eulerization using this idea, together with trial and error and some ingenuity.
Finding Good Eulerizations
Suppose we want an optimal procedure for eulerizing a graph. What theoretical ideas and methods could we use to build such a tool?
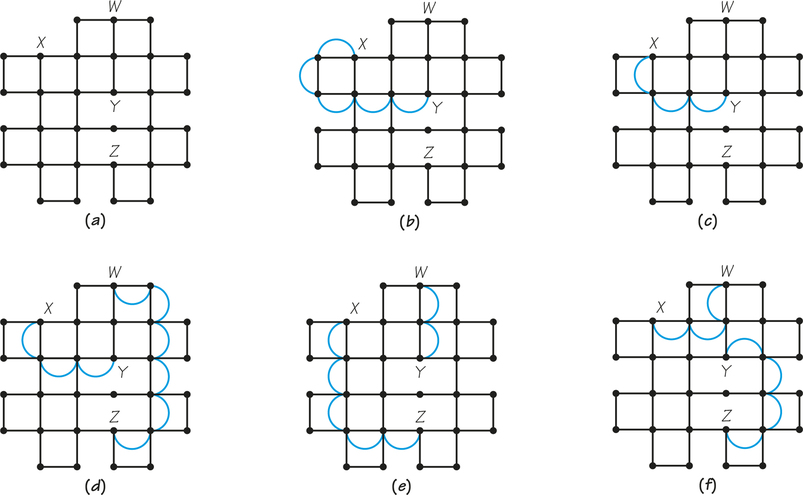
One building block we could use is a method for finding the shortest path between two given vertices of a graph. For example, let us focus on vertices X and Y in Figure 1.18a. Both have odd valence. We can connect them with a pattern of duplicate edges, as in Figure 1.18b. The cost of this is the length of the path we duplicated from X to Y. A shorter path from X to Y, such as the one shown in Figure 1.18c, would be better. Fortunately, the shortest-path problem has been well studied, and we have many good procedures for solving it exactly, even in large, complex graphs.
But there is more to eulerizing the graph in Figure 1.18a than dealing with X and Y. Notice that we have odd valences at Z and W. Should we connect X and Y with a path, and then connect Z and W, as in Figure 1.18d? Or should we connect X to Z and Y to W, as in Figure 1.18e? Another alternative is to use connections X to W and Y to Z, as in Figure 1.18f. It turns out that the alternatives in both Figures 1.18e and 1.18f are preferable to the one in Figure 1.18d because they involve seven added edges, whereas Figure 1.18d uses nine.
We know there is a simple way to test whether a connected graph has an Euler circuit: Check to see if the graph is even-valent. Is there a very easy way to compute the number of edges in a best eulerization of a graph? Unfortunately, the answer is “no.” However, there is a simple observation that often saves a lot of work. Suppose we count the number of odd-valent vertices in a graph. This number must always be an even number. When we duplicate an existing edge, we can never change more than two odd-valent vertices to even-valent vertices. Thus, in a best eulerization of a graph, the number of edges that must be duplicated is at least the number of odd-valent vertices divided by two. If, for example, we have a graph with 10 odd-valent vertices and we find an eulerization with five added edges, there may be other eulerizations that also have five duplicated edges, but there can be no eulerization with fewer than five duplicated edges.
Remember that when an unweighted graph is eulerized in an optimal way, then the total cost of traversing each edge at least once can be found by adding the total number of edges in the graph to the number of edges that are reused (duplicated). Small problems involving eulerization can be carried out by trial-and-error methods. Unfortunately, although there is an algorithm that can be applied to find the best eulerization for large problems, the details of this algorithm are quite complex. However, the procedure works quickly not only for graphs without weights but also for graphs with weights on the edges.
Self Check 2
- Does the graph in Figure 1.12b have an Euler circuit? (If so, write down the Euler circuit.)
- No. Though the graph is connected, its vertices are not all even-valent.
- If the graph does not have an Euler circuit, what is the minimum number of duplicated edges required for a best possible eulerization?
- By duplicating one edge, we get a new graph, all of whose vertices are even-valent.