1.5 1.4 Urban Graph Traversal Problems
Euler circuits and eulerizing have many more practical applications than just checking parking meters. Almost any time services must be delivered along streets or roads, our theory can make the job more efficient. Examples include collecting garbage, salting icy roads, plowing snow, inspecting subway or railroad tracks for flaws, collecting debris or leaves from urban curbs, mowing grass along superhighways, or reading electric meters at private houses (see Spotlight 1.3).
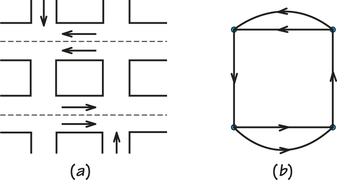
Each of these problems has its own special requirements that may call for modifications in the theory. For example, in the case of garbage collection, the edges of our graph represent streets, not sidewalks. If some of the streets are one-way, we need to put arrows on the corresponding edges, resulting in a directed graph, or digraph. The circuits we seek will have to obey these arrows. In the case of salt spreaders and snowplows, each lane of a street needs to be modeled as a directed edge, as shown in Figure 1.19. Note that the arrows on the map and digraph are not in color because these arrows denote restrictions in traversal possibilities, not parts of circuits.
Like salt spreaders, street-sweeping trucks can travel in only one lane at a time and must obey the direction of traffic. Street sweepers, however, have an additional complication: parked cars. It is very difficult to clean the street if cars are parked along the curb. Yet for overall efficiency, those who are responsible for routing street sweepers want to interfere with parking as little as possible. The common solution is to post signs specifying times when parking is prohibited. Because the parking-time factor is a constraint on street sweeping, it is important to find not only an Euler circuit, or a circuit with very few duplications, but also a circuit that visits streets when they are free of cars. Once again, mathematicians have developed techniques to handle this constraint.
Israel Electric Company Reduces Meter-Reading Task 1.3
1.3
Electric meters and icy roads don’t seem to have much in common, but private companies and governments can draw on a common source—mathematics—to save customers money and drivers from accidents. Thus, in Israel there was a branch of the major electric company that needed to make the job of reading its electric meters more efficient, while in Minnesota and Ohio, the counties and cities must plow and/or de-ice winter roads. Both problems start in the same place: constructing a graph theory model of the streets and roads the meter readers need to traverse and winter maintenance vehicles must travel. Next, applying the ideas about the Chinese Postman problem for efficiently providing services along the edges of a graph at least once can lead to time-saving routes for meter reading or de-icing. Because the customers of the electric company change as new houses and businesses need service and because the roads needing plowing vary with storm patterns, digitized versions of street networks are usually now maintained online; solutions to either the Chinese Postman problem or variants of it can be solved in real time. In Minnesota and Ohio, routes are typically reevaluated every winter season. In one Ohio county where nearly 200 segments of road involving about 300 miles need plowing, the number of trucks involved was reduced by 30% and the time to do the work was cut 40% when Chinese Postman ideas were used. In Israel, meter reader routes could be traversed in 40% less time and deadheading time was reduced to 1% of the time spent by using Chinese Postman algorithms.
Finally, because towns and cities of any size have more than one street sweeper, parking officer, garbage truck, or pothole-filling crew, a single best route may not suffice. Instead, it becomes necessary to divide the territory into multiple routes. The general goal is to find optimal solutions while taking into account traffic direction, number of lanes, parking-time restrictions, and divided routes (see Figure 1.20).
Management science makes all this possible. For example, a pilot study done in the 1970s in New York City showed that applying these techniques to street sweepers in just one district could save about $30,000 per year. With 57 sanitation districts in New York, this would amount to a savings of more than $1.5 million in a single year. This translates to over $6 million in today’s dollars. In addition, the same principles could be extended to garbage collection, parking control, and other services carried out on street networks.

This plan was not adopted when first proposed. Because city services take place in a political context, several other factors come into play. For example, union leaders try to protect the jobs of city workers, certain bureaucrats try to keep their departmental budgets high, and elected politicians rarely want to be accused of cutting the jobs of their constituents. Thus, political obstacles can overrule management science. As mentioned in Spotlight 1.2 on page 10, such human factors often arise when applying management science. Perhaps a more acceptable street- sweeping plan would have been devised for New York City if more attention had been paid to the human factors earlier.
Despite the complications of real-world problems, management science principles provide ways to understand these problems by using graphs as models. We can reason about the graphs and then return to the real-world problem with a workable solution. The results we get can have a lasting effect on the efficiency and economic well-being of any organization or community.