Chapter 1 Exercises
Chapter 1 Exercises
1.1 Euler Circuits
1.2 Finding Euler Circuits
Question 1.31
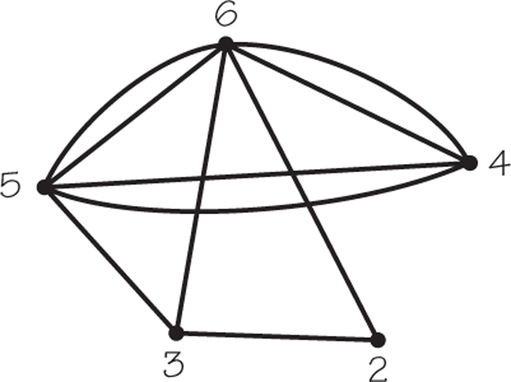
1. Refer to the accompanying graph G (which might represent the two-way streets of a small housing subdivision).
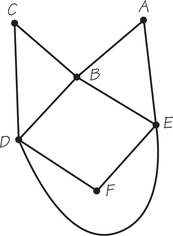
- Determine the number of vertices.
- Determine the number of edges.
1.
(a) Six vertices
(b) Nine edges
Question 1.32
2. Use the diagram for graph G in Exercise 1.
- Find two ways to get from C to A by traversing four edges.
- Find two ways to get from C to A by traversing three edges.
- Find two ways to start at B and return to B, traversing four edges.
Question 1.33
3.
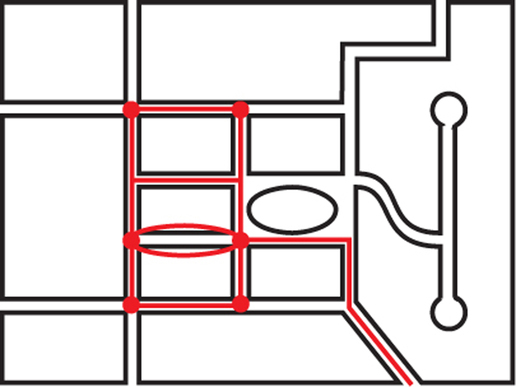
- Locate within Figure 1.3a a section of the street network shown that indicates how the graph below could be interpreted as meters that require inspection in this urban street layout.
- Can you find a tour of the edges in the graph shown above that starts at A and allows for inspection of the parking meters with as few deadheaded edges as possible?
3.
(a)
(b) ADGIJHKLMLKHGHEDEBA (other answers possible)
Question 1.34
4.
- Determine the number of vertices and edges in the accompanying graph G.
- What is the smallest number of edges that must be added to graph G so that the result is a connected graph?
- What are the valences of the vertices in G?
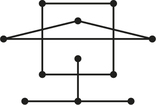
Question 1.35
5.
- Is the figure below a graph? Explain your answer.
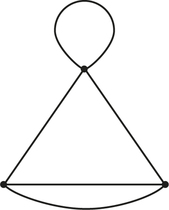
- The graph below has edges that “cross” at points that are not vertices of the graph. Which edges are these?
- How many vertices and edges are there in the preceding graph?
5.
(a) No
(b) EC, AD, BD, and AC
(c) Five vertices; six edges
Question 1.36
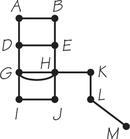
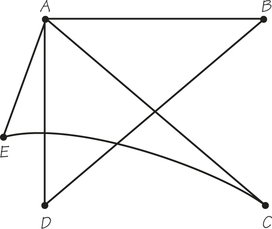
6. The graph below shows the stores and roads connecting them in a small shopping mall.
- How many stores does the mall have?
- How many roads connect up the stores in the mall?
- Write down a path from C to F.
- Write down a path from E to B.
Question 1.37
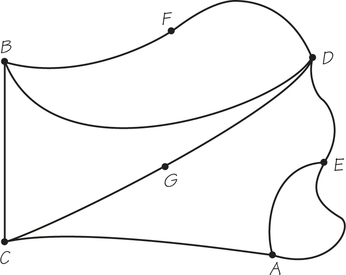
7. In the accompanying graph, the vertices represent houses and two vertices are joined by an edge if it is possible to drive between the two houses in under 10 minutes.
- How many vertices does the graph have?
- How many edges does the graph have?
- What are the valences of the vertices in this graph?
- Based on the information given by the graph, for which houses, if any, is it possible to drive to all the other houses in less than 20 minutes?
- Based on the graph, from house B which houses require a trip of longer than 20 minutes?
7.
(a) Eight vertices
(b) 13 edges
(c) A: 4; B: 2; C: 3; D: 3; E: 4; F: 4; G: 3; H: 3
(d) A, D, and F
(e) E, G, and H
Question 1.38
8.
- Redraw the graph in Figure 1.2a to obtain a graph that has the same information but where the edges meet other edges only at vertices.
- List all the routes that start on the U.S. side of the Atlantic Ocean and cross the ocean once and immediately.
Question 1.39
9. In the graph below, the vertices represent cities and the edges represent roads connecting them. What are the valences of the vertices in this graph? (Keep in mind that E is part of the graph.) What might the valence of city E be showing about the geography?
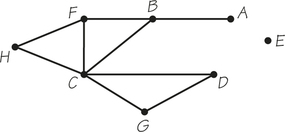
9.
E: 0; A: 1; H, D, and G: 2; B and F: 3; C: 5. E might be on an island and have no road access to the other cities.
Question 1.40
10. In the three graphs below, the vertices represent cities and the edges represent roads connecting them. In which graphs could a person located in city A choose any other city and then find a sequence of roads to get from A to that other city?
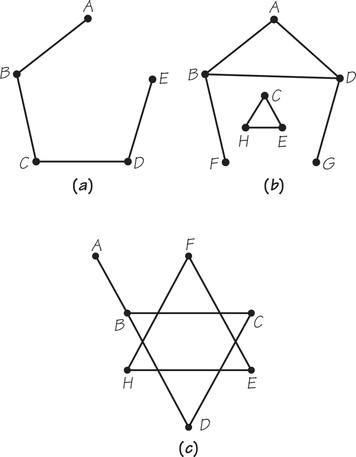
Question 1.41
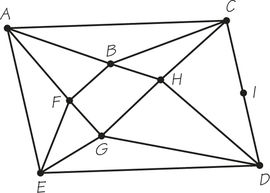
11.
- How many vertices and edges does the graph in Figure 1.6 have?
- How many vertices and edges does the graph in Figure 1.7 have?
- How many vertices and edges does the graph in Figure 1.8a have?
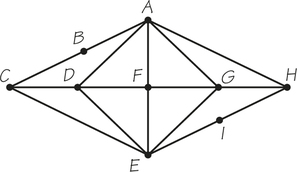
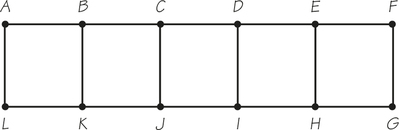
11.
(a) 5; 5
(b) 7; 6
(c) 10; 14
Question 1.42
12. Jack and Jill are located in Miami and want to fly to Berlin (see Figure 1.2).
- Find three paths for them to carry out this trip.
- What is the largest number of paths that can be used to carry out this trip that do not repeat a vertex (city)?
- Explain why it is reasonable not to want to repeat a vertex in this situation.
Question 1.43
13. Refer to the figure in Exercise 6.
- Write down a circuit that includes the vertices G and D but does not start or end at either of these vertices.
- If two paths are considered different if they use different edges, write down
- two different paths from B to D.
- three different paths from C to F.
- a circuit that has four edges.
13.
(a) CGDBC (Answers can vary.)
(b) (i) BD; BFD
(ii) CBF; CGDF; CGDBF
(iii) GDBCG (Answers can vary.)
Question 1.44
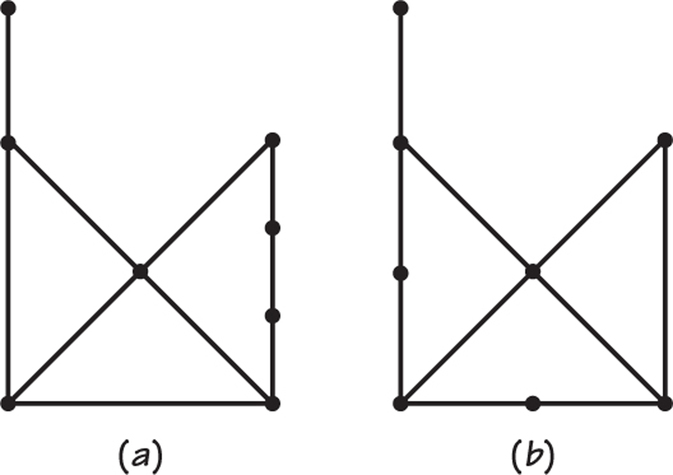
14. In the graphs in Figure 1.17, find the smallest possible number of edges you could remove that would disconnect the graph.
Question 1.45
15. Draw a graph with eight vertices that is connected where each vertex has
- degree (valence) 2.
- valence 3.
- valence 4.
- Do all graphs with eight vertices having valence 2 have the same number of edges?
15.
Drawings can vary. Possible renderings for parts (a) through (c) include the following:
(a)

(b)
(c)
(d) Yes
Question 1.46
16.
- Add up the numbers you get for the valences of the vertices in Figure 1.6.
- Add up the numbers you get for the valences of the vertices in Figure 1.7.
- Add up the numbers you get for the valences of the vertices in Figure 1.8a.
- Describe the pattern you see in your answers for parts (a) through (c).
- Show that the pattern describes a fact that is true for any graph. (Hint: How many endpoints does an edge have?)
Question 1.47
17. In the graph in Figure 1.8a, find the smallest possible number of edges you could remove that would disconnect the graph.
17.
2
Question 1.48
18.
- Can you draw a graph with at least two vertices for which all the vertices have different valences?
- Can you do this so that the valences are consecutive integers?
Question 1.49
19.
- Can you draw a graph that is connected and for which the valences of vertices are the consecutive integers from 2 to 6?
- If a graph such as the one described in part (a) exists, can it have an Euler circuit? (Explain your answer.)
19.
(a)
(b) No. To have an Euler circuit a graph cannot have odd-valent vertices.
Question 1.50
20.
- What is the number of vertices and edges in the accompanying graph G?
- Write down an Euler circuit for the accompanying graph, first by numbering the edges consecutively starting at an edge emanating from vertex D and then using an alternative description that lists the vertices as they are traversed by the Euler circuit.
Question 1.51
21. Draw a graph that is not connected with eight vertices, all of whose vertices have valence 2.
21.
Drawings can vary. Possible renderings include the following:

Question 1.52
22.
- Is it possible that a street network gives rise to a disconnected graph? If so, draw such a network of blocks and streets and parking meters (in the style of Figure 1.12a). Then draw the disconnected graph it gives rise to.
- Draw a graph where every vertex has valence of at least 3 but where removing a single edge disconnects the graph.
- In what urban settings might a road network be represented by a graph that has an edge whose removal would disconnect the graph?
Question 1.53
23.
- Find a graph of eight vertices in which the valences of the vertices are 1, 2, 2, 2, 3, 3, 3, 4.
- Find a graph with the same valences as the one you found in part (a) but that is “different” from the one in part (a).
23.
Drawings can vary. Possible renderings include the following:
Question 1.54
24. For some urban services provided along streets, it may matter whether the roads are one-way or two-way. Give some examples where the street directions do and do not matter for our graph model analysis.
Question 1.55
![]() 25. A postal worker is supposed to deliver mail on all streets represented by edges in the accompanying graph by traversing each edge exactly once. The first day, the worker traverses the numbered edges in the order shown in graph (a), but the supervisor is not satisfied—why? The second day the worker follows the path indicated in graph (b), and the worker is unhappy—why? Is the original job description realistic? Why?
25. A postal worker is supposed to deliver mail on all streets represented by edges in the accompanying graph by traversing each edge exactly once. The first day, the worker traverses the numbered edges in the order shown in graph (a), but the supervisor is not satisfied—why? The second day the worker follows the path indicated in graph (b), and the worker is unhappy—why? Is the original job description realistic? Why?
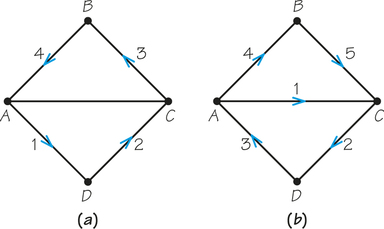
25.
With part (a), not all edges are traveled by the worker. With part (b), the end of the route is not the same as the beginning of the route. The description is not realistic because there is no Euler circuit in the graph.
Question 1.56
26. For the street network in Exercise 25, draw the graph that would be useful for routing a snowplow. Assume that all streets are two-way, one lane in each direction, and that you need to pass down each lane separately.
Question 1.57
27. Find an efficient route for the snowplow to follow in the graph you drew in Exercise 26.
27.
Since this graph is connected and even-valent, it has an Euler circuit. Any Euler circuit will solve the problem efficiently.
Question 1.58
28.
- Give examples of services that could be performed by a vehicle that moved in the direction of traffic down either lane of a two-way street.
- Give examples of services that would probably require a vehicle to travel down each of the lanes of a two-way street (in the direction of traffic for that lane) to perform the service.
Question 1.59
29. For the street network shown below, draw the graph that would be useful for finding an efficient route for checking parking meters. (Hint: Notice that not every sidewalk has a meter; see Figure 1.12.)

29.
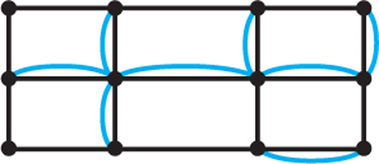
Question 1.60
30.
- For the street network in Exercise 29, draw a graph that would be useful for routing a garbage truck. Assume that all streets are two-way and that passing once down a street suffices to collect from both sides.
- Do the same problem as in part (a), using the assumption that one pass down the street suffices to collect from only one side.
Question 1.61
31.
- In the accompanying graph, find the largest number of paths from A to C that do not have any edges in common.

- Verify that the largest number of paths with no edges in common between any pair of vertices in this graph is the same.
- Why might we want to be able to design graphs such that we can move between two vertices of a graph using paths that have no edges in common?
31.
(a) 3
(b) Answers will vary.
(c) Answers will vary.
Question 1.62
32. Examine the paths represented by the numbered sequences of edges in both parts of the figure below. Determine whether each path is a circuit. If it is a circuit, determine whether it is an Euler circuit.
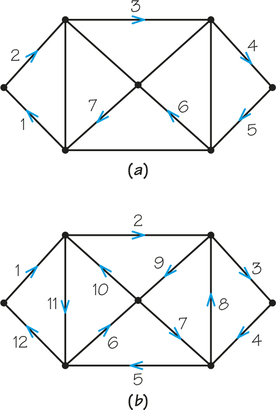
Question 1.63
33. The company that distributes natural gas in a small town is located at vertex C in the accompanying graph G, which models the two-way streets for the town.
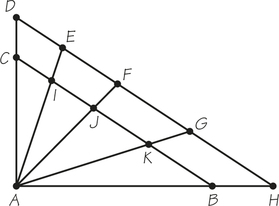
- Can an inspector for gas leaks travel along the street network and find a route that starts and ends at C and has no deadheads (repeated edges)?
- What is the minimum number of repeated edges in a shortest-length tour T, starting and ending at C, that looks for gas leaks?
- By duplicating existing edges in G, use tour T to modify graph G to obtain a new graph G*, which shows that T can be interpreted as an Euler circuit in G*.
33.
(a) No
(b) 4
(c) Answers will vary. One solution would involve duplicating edges CD, DE, FG, and AB in the accompanying graph.
Question 1.64
34. In Figure 1.8b, suppose we started an Euler circuit using this sequence of edges: 14, 13, 8, 1, 4 (ignore existing arrows on the edges). What does our guideline for finding Euler circuits tell you not to do next?
Question 1.65
35. In Figure 1.13c, suppose we started an Euler circuit using this sequence of edges: 6, 7, 8, 9 (ignore existing arrows on the edges). What does our guideline for finding Euler circuits tell you not to do next?
35.
Do not choose edge 2, but edges 1 or 10 could be chosen.
Question 1.66
36. Find Euler circuits in the right-hand graphs in Figures 1.17a and 1.17b.
Question 1.67
37. Find an Euler circuit on the graph of Figure 1.15c (including the blue edges).
37.
Answers will vary.
Question 1.68
38. An Euler circuit visits a four-valent vertex X, such as the one in the accompanying graph, by using the edges AX and XB consecutively, and then using CX and XD consecutively. When this happens, we say that the Euler circuit cuts through at X.
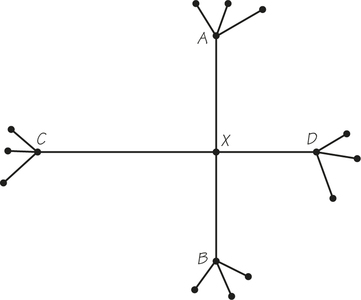
Suppose G is a four-valent graph such as that in the diagram below. Is it possible to find an Euler circuit of this graph that never cuts through any vertex? Explain why it might be desirable to find an Euler circuit of this special kind in an applied situation.

Question 1.69
39.
- Which vertices in the accompanying graph are odd-valent?
- In the accompanying graph, we see a territory for a parking-control officer that has no Euler circuit. How many sidewalks (edges) need to be omitted in order to enable us to find an Euler circuit? What effect would this have in the associated real-world situation?
39.
(a) A, C, E, and H are odd-valent.
(b) 2
1.3 Beyond Euler Circuits
1.4 Urban Graph Traversal Problems
Question 1.70
40. Squeeze the circuit shown in graph (a) below onto graph (b). Show your answers by writing numbered arrows on the edges and by listing a sequence of vertices (for example, ABEB … A).
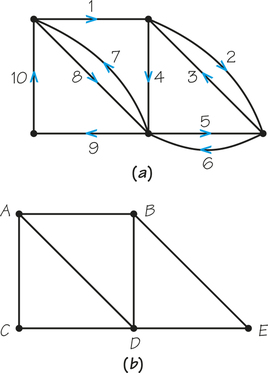
Next, squeeze the circuit shown in graph (c) onto graph (d). Show your answers by writing numbered arrows on the edges and by listing a sequence of vertices.
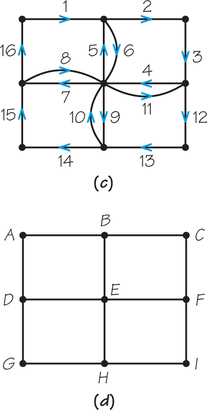
Question 1.71
41. Find an Euler circuit on the eulerized graph (b) of the accompanying figure. Use it to find a circuit on the original graph (a) that covers all edges and reuses edges only five times. Can fewer than five reused edges be achieved?
41.
Answers will vary; no.
Question 1.72
42. In the accompanying graph, add one or more edges to produce a graph that has an Euler circuit.
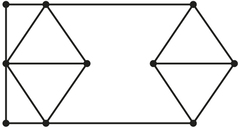
Question 1.73
43. A college campus has a central square with sides arranged as shown by the edges in the graph below. Show how all these sidewalks can be traversed at least once in a tour that starts and ends at the same vertex.
43.
Answers will vary. Possible answers include AECDABDCBEA.
Question 1.74
44. Find a circuit in the accompanying graph that covers every edge and has as few reuses as possible.

Question 1.75
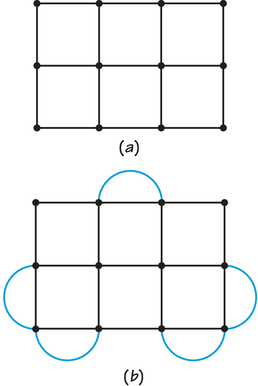
45. Eulerize the following rectangular street networks using the same patterns that would be used by the edge walker described on page 18.
- A 5 × 5 rectangle
- A 4 × 5 rectangle
- A 6 × 6 rectangle
- Can you find an eulerization with nine added edges for a 2-by-7-block rectangular street network? Can you do better than nine added edges?
45.
Drawings can vary. Possible renderings for parts (a), (b), and (c) include the following:
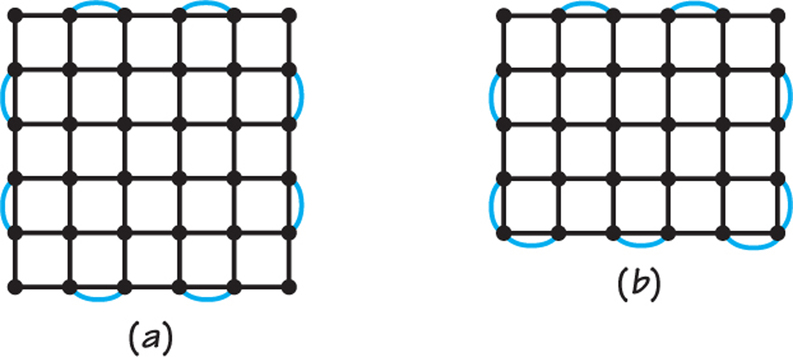
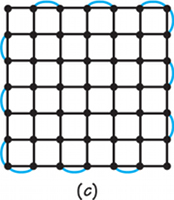
(d) Yes; no
Question 1.76
46. Find good eulerizations for the accompanying graphs, using as few duplicated edges as you can. See “Finding Good Eulerizations” (page 19) for hints.

Question 1.77
47.
- Determine the minimum number of edges in the graph that have to be removed for the resulting graph to have all even-valent vertices.
- Does the graph you obtain in part (a) have an Euler circuit?
- Determine the minimum number of edges in the graph that have to be removed for the resulting graph to have all even-valent vertices.
- Does the graph you obtain in part (c) have an Euler circuit?
47.
(a) 2
(b) Yes
(c) 2
(d) No
Question 1.78
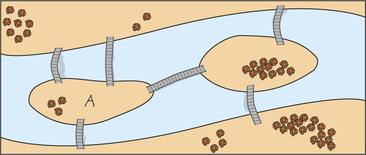
48. The following figure shows a river, some islands, and bridges connecting the islands and riverbanks. A charity is sponsoring a race in which entrants have to start at A, go over each bridge at least once, and end at A. Draw a graph that would be useful for finding a route that requires the least recrossing of bridges. Show what that route would be. (Historical note: This situation resembles the one that inspired Leonhard Euler’s 1736 “recreational mathematics” problem that resulted in the first work in graph theory.)
Question 1.79
49. On Wednesdays during the summer, a small town that has only two-way streets does not allow on-street parking in the mornings. A truck that flushes water onto the streets to clean off “debris” can thus easily perform its work.

- For the street network of the town shown in the preceding graph, design an efficient route R for the truck starting and ending at vertex A.
- If all the edges take equally long and take 9 minutes to cover when flushing is being carried out and 7 minutes when deadheading, how long does it take for route R to be traversed?
49.
(a) ADEADCAFCFBA
(b) 95 minutes
Question 1.80
50.
- Discuss the difference between these two problems:
- Adding the minimum number of edges to a graph to make all its vertices even-valent
- Finding the best eulerization of a connected graph
- In (i), must the graph that results from adding a minimum number of edges to make all the vertices even-valent have an Euler circuit?
Question 1.81
51. Draw a graph with exactly two odd-valent vertices, which requires exactly nine edges to be duplicated in order to find the best eulerization of the graph.
51.

Question 1.82
52. In the following graph, the outer blocks are 1000-by-1000 feet, and the middle blocks are 1000-by-4000 feet. Find a circuit of minimum total length that covers all edges.

Question 1.83
53. In the graph below, the outer blocks are 1000-by-1000 feet, and the middle blocks are 1000-by-4000 feet. Find a circuit of minimum total length that covers all edges.

53.
There are many circuits that achieve a minimum length of 44,000 feet.
Question 1.84
54.
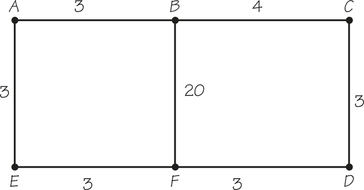
- Find the cheapest route in the accompanying graph, where one starts at vertex A, finishes at vertex A, and traverses each edge at least once. The cost of a route is computed by summing the numbers along the edges that one uses.
- How many edges are repeated in the minimal-cost route?
- Discuss the implications of this example for the relation between finding good eulerizations of graphs and the problem of finding cheap routes that start and end at the same vertex and traverse each edge at least once.
- The physical edge with cost 20 in the diagram is not physically longer than other edges with lower costs attached to them. Explain why in an urban setting it might make sense to assign two stretches of street of similar length very different “costs” for traversing them.
- What are some different meanings that “weights” (for example, traffic volume) potentially assigned to edges in a graph might have in an urban setting?
Question 1.85
55. Which of the accompanying graphs have Euler circuits? In the ones that do, find the Euler circuits by numbering the edges in the order the Euler circuit uses them. For the ones that don’t, explain why no Euler circuit is possible.
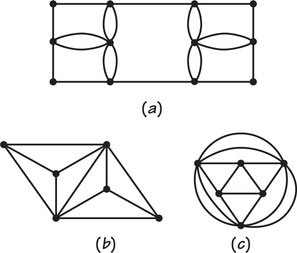
55.
Graphs (a) and (c); additional answers will vary.
Question 1.86
56. Eulerize the accompanying graph by using four new edges. Find an Euler circuit in the eulerized graph and use that circuit to find a circuit of the original graph that covers all edges but reuses edges only four times. How many different ways can the four edges be chosen? What is the total number of edges in the Euler circuit in the eulerized graph?
Question 1.87
57. A graph G represents a street network to be traveled by a postal worker on foot, who must deliver mail to the houses on both sides of each street. How does one obtain from G a new graph H that represents the sidewalks that must be traversed? Does graph H always have an Euler circuit? Explain your answer.
57.
For each edge e of G, add another edge joining the vertices that are endpoints of e to obtain H. If G is connected, H does have an Euler circuit because whatever the valences of G, graph H has valences that are doubles of these and remains connected. Hence, H is even-valent and connected.
Question 1.88
58. In the following graph, find a circuit that covers every edge and has as few reuses as possible.
Question 1.89
59.
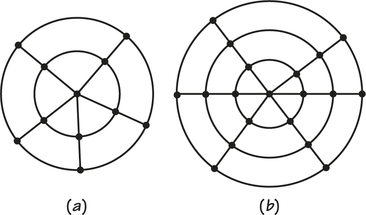
- Find the best eulerizations you can for the two accompanying graphs.
- Graph (a) can be thought of as having five rays and two circles, and graph (b) as having six rays and three circles. Draw a graph with four rays and four circles and find the best eulerization you can for this graph.
- Find a “formula” involving r and s for the smallest number of edges needed to eulerize a graph of this type having r rays and s circles.
59.
(a) Drawings can vary. Possible renderings include the following:
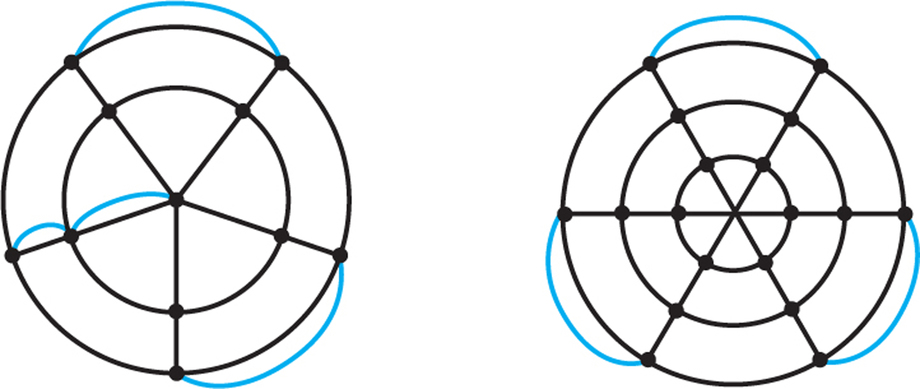
(b) The best eulerization for the four-circle, four-ray case adds two edges.
(c) Answers will vary.
Question 1.90
![]() 60. Suppose that for a certain connected graph, it is possible to disconnect it by removing one edge. Explain why such a graph (before the edge is removed) must have at least one vertex of odd valence. (Hint: Show that it cannot have an Euler circuit.)
60. Suppose that for a certain connected graph, it is possible to disconnect it by removing one edge. Explain why such a graph (before the edge is removed) must have at least one vertex of odd valence. (Hint: Show that it cannot have an Euler circuit.)
Question 1.91
61.
- Can you draw a graph with six vertices where the valence of each vertex is 5?
- If such a graph exists, how many edges must it have?
61.
(a) Yes
(b) 15
Question 1.92
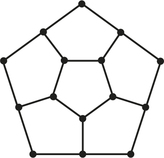
62. Each of the accompanying graphs represent the sidewalks to be cleaned in a fancy garden (one pass over a sidewalk will clean it). Can the cleaning be done using an Euler circuit? If so, show the circuit in each graph by numbering the edges in the order the Euler circuit uses them. If not, explain why no Euler circuit is possible.
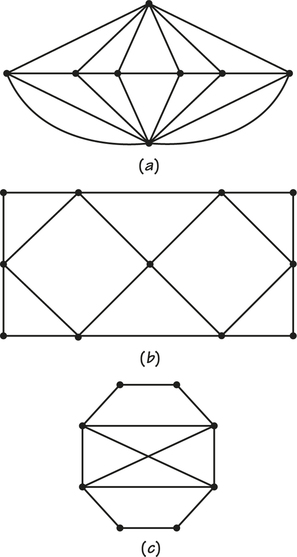
Question 1.93
![]() 63. If an edge is added to an already existing graph, connecting two vertices already in the graph, explain why the number of vertices with odd valence has the same parity before and after. (This means that if it was even before, it is even after, while if it was odd before, it remains odd.)
63. If an edge is added to an already existing graph, connecting two vertices already in the graph, explain why the number of vertices with odd valence has the same parity before and after. (This means that if it was even before, it is even after, while if it was odd before, it remains odd.)
63.
Answers will vary.
Question 1.94
![]() 64. Any graph can be built in the following fashion: Put down dots for the vertices and then add edges connecting the dots as needed. When you have put down the dots, and before any edges have been added, is the number of vertices with odd valence an even number or an odd number? What is the number of vertices with odd valence when all the edges have been added (see Exercise 63)?
64. Any graph can be built in the following fashion: Put down dots for the vertices and then add edges connecting the dots as needed. When you have put down the dots, and before any edges have been added, is the number of vertices with odd valence an even number or an odd number? What is the number of vertices with odd valence when all the edges have been added (see Exercise 63)?
Question 1.95
65. Draw the graph for the parking-control territory shown in the figure below. Label each vertex with its valence and determine whether the graph is connected.
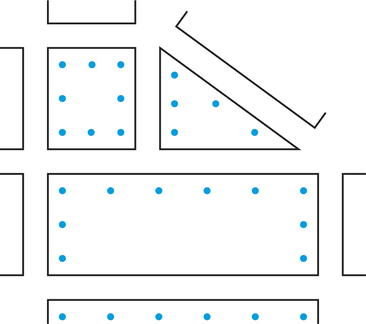
65.

Question 1.96
66. If a rectangular street network is r blocks by s blocks, find a formula for the minimum number of edges that must be added to eulerize a graph representing the network in terms of r and s. (Hint: Treat the case r=1 separately. Test your formula with the cases 6 blocks by 5 blocks, 6 blocks by 6 blocks, and 5 blocks by 3 blocks.)
Question 1.97
![]() 67. The word valence is also used in chemistry. Find out what it means in chemistry, and explain how this usage is similar to its use here.
67. The word valence is also used in chemistry. Find out what it means in chemistry, and explain how this usage is similar to its use here.
67.
Answers will vary.
Question 1.98
![]() 68. For the street network below, draw a graph that represents the sidewalks with meters. Find the minimum-length circuit that covers all sidewalks with meters. If you drew the graph as we recommended, you would find that the shortest circuit has length 18 (it reuses every edge).
68. For the street network below, draw a graph that represents the sidewalks with meters. Find the minimum-length circuit that covers all sidewalks with meters. If you drew the graph as we recommended, you would find that the shortest circuit has length 18 (it reuses every edge).
But the meter checker comes to you and says, “I don’t know anything about your theories, but I have found a way to cover the sidewalks with meters using a circuit of length 10. My trick is that I don’t rule out walking on sidewalks with no meters.” Explain what he means and discuss whether his strategy can be used in other problems.
Question 1.99
69. Each edge of the accompanying graph represents a two-lane highway. A grass-mowing machine is located at A, and its operator has the job of cutting the grass along each of the edges of road shown. Find a tour for the mowing machine that begins and ends at A. Find a tour that begins and ends at A and, as the mowing is done, moves along the edge of the road in the same direction as the traffic.
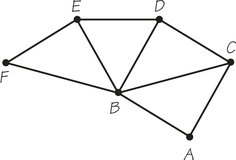
69.
Answers will vary. A possible answer is ABDEFBEBFEDBACDCBCA.
Question 1.100
70. Draw a graph with exactly two vertices of valence 3 and a minimal but positive number of 4-valent vertices, which can be eulerized by adding one edge.
Chapter Review
Question 1.101
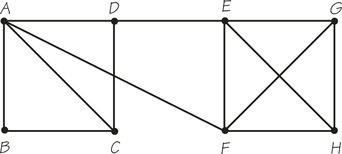
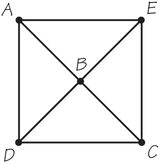
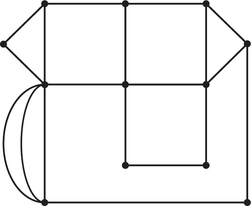
71. Answer the following questions for graph G below, which was created to represent the roads of a shopping mall.
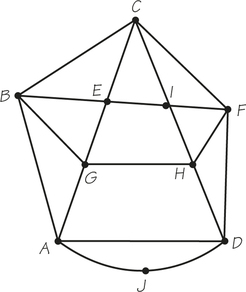
- Determine the number of vertices and edges of the graph.
- Determine the valences of the vertices A, F, and D.
- If the graph has an Euler circuit, write it down starting with vertex E.
71.
(a) 10 vertices; 19 edges
(b) A has valence 4; F has valence 4; D has valence 4.
(c) There are Euler circuits. Answers will vary.
Question 1.102
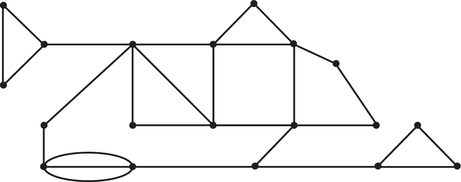
72. Answer the following questions for accompanying graph G, which is used to model roads that must be inspected for potholes.
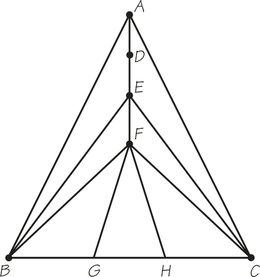
- How many odd-valent vertices does G have?
- If G has an Euler circuit, write it down.
- If G does not have an Euler circuit, what is the minimum number of edges that must be repeated to find a tour of G that starts and ends at C and traverses each edge of G at least once?
- How does your answer to part (c) relate to the answer to part (a)?
