20.3 20.2 Tilings with Irregular Polygons
What about edge-to-edge tilings with irregular polygons, which may have some sides longer than others or some interior angles larger than others? We will look just at monohedral tilings (in which all tiles have the same size and shape) and investigate, in turn, which triangles, quadrilaterals (four-sided polygons), hexagons, and so forth can tile the plane.
In the most general shape of a triangle, all sides are of different lengths and all interior angles of different sizes. Such a triangle is called a scalene triangle, from the Greek word for “uneven.” We can always take two copies of any triangle and fit them together to form a parallelogram, a quadrilateral whose opposite sides are parallel (Figure 20.6a). It’s easy to see that we then can use such parallelograms to tile the plane by making strips and then fitting together layers of strips edge-to-edge (Figure 20.6b).
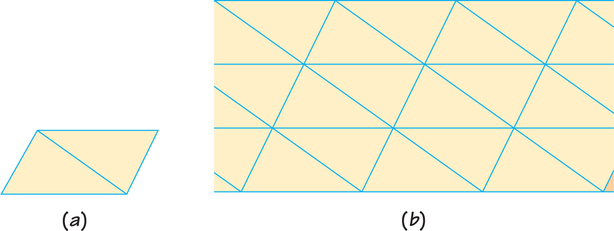
Tiling with a Triangle THEOREM
Any triangle whatsoever—whether it has three sides equal, two sides equal, or no sides equal—can tile the plane.
What about quadrilaterals? We have seen that squares can tile the plane, and rectangles certainly can, too. We have just noted that any parallelogram can tile. What about a quadrilateral with its opposite sides not parallel, as in Figure 20.7a? The same technique as for triangles will work. We fit together two copies of the quadrilateral, forming a hexagon whose opposite sides are parallel. Such hexagons fit next to each other to form a tiling, as in Figure 20.7b.

The quadrilaterals shown in Figure 20.7 are all convex, meaning that if you take any two points on the tile (including the boundary), the line segment joining them lies entirely within the tile (again, including the boundary). The quadrilateral of Figure 20.8a is not convex, but the same technique works to form a tiling (Figure 20.8b).
Convex DEFINITION
A tile (including its boundary) is convex if for any two points on it, all the points on the line segment joining them also belong to the tile.
Tiling with a Quadrilateral THEOREM
Any quadrilateral, even one that is not convex, can tile the plane.

We could hope that such success would extend to irregular polygons with any numbers of sides, but it doesn’t. Which convex hexagons can tile the plane was determined by Karl Reinhardt (1895–1941) in his 1918 doctoral thesis. He showed that for a convex hexagon to tile, it must belong to one of three classes. Examples of the three classes are shown in Figure 20.9. Tilings with a hexagon of type 2 use both ordinary and mirror-image versions of the hexagon.
Tiling with a Hexagon THEOREM
Exactly three classes of convex hexagons can tile the plane.
Reinhardt also explored tilings by convex pentagons and found five classes that tile. For example, any pentagon with two parallel sides can tile. Reinhardt did not complete the solution, as he did for hexagons, by proving conclusively that no other pentagons could tile. He claimed that it would be very tedious to finish the analysis. Still, he felt that he had found them all. In 1968, after 35 years of working on the problem on and off, R. B. Kershner, a physicist at Johns Hopkins University, discovered three more classes of pentagons that tile. Kershner, in turn, was sure that he had found all pentagons that tile; but, like Reinhardt, he did not offer a complete proof, which “would require a rather large book.”

When an account of the alleged “complete” classification into 8 types appeared in the July 1975 issue of Scientific American, the article provoked an amateur mathematician to discover a 9th type! Marjorie Rice, a housewife with no formal education in mathematics beyond high school “general mathematics” taken 36 years earlier, devised her own mathematical notation and found four more types (see Spotlight 20.2). A 14th type was found by a mathematics graduate student in 1985. In July 2015, a 15th type was discovered by researchers at the University of Washington Bothell who used a computerized search. No one knows if that completes the classification.
With the situation so intricate for convex pentagons, you might think that it must be still worse for polygons with seven or even more sides. In fact, however, the situation is remarkably simple, as Reinhardt proved in 1927.
Tiling with a Polygon with More Sides THEOREM
A convex polygon with seven or more sides cannot tile.
In Praise of Amateurs 20.2
20.2
R. B. Kershner’s claim to have found all convex pentagons that tile was read by many puzzle enthusiasts, including Richard James III and Marjorie Rice. James found a tiling that Kershner had missed.

Rice, a San Diego housewife and mother of five, read about Jamess new tile. I thought I would see if I could find still another type. It was a delightful new puzzle to me.”
With no formal education in mathematics beyond a general mathematics course in high school, she not only worked out her own method of attack, but she invented her own notation as well.
“I began drawing little diagrams on my kitchen counter when no one was there, covering them up quickly if someone came by, for I didn’t wish to have to explain what I was doing. I was searching for a new type, and a few weeks later, I found it.” Over the next two years, she found three additional new tilings.
Rice was born in 1923 in St. Petersburg, Florida, and went to a one-room country school.
“When I was in the sixth or seventh grade, our teacher pointed out to us the golden section in the proportions of a picture frame. This immediately caught my imagination and I never forgot it. I’ve … been especially interested in architecture and the ideas of architects and planners such as Buckminster Fuller. I’ve come across the golden section again in my reading and considered its use in painting and design.” (The golden ratio is discussed in Chapter 19, on pages 783–790.)
After high school, Rice worked until her marriage in 1945. She was drawn back into mathematics by her children, finding solutions to their homework problems “by unorthodox means, since I did not know the correct procedures.” She became especially interested in textile design and the works of M. C. Escher. As she pursued the pentagonal tilings, she produced some imaginative Escher-like patterns. (You can see some of them at one of the Suggested Websites for this chapter.)


What makes a person pursue a problem so patiently and persistently? Marjorie Rice was not trained for it, nor was she paid, but she gained great personal satisfaction from the pursuit.
Intense spirit of inquiry and keen perception are the forte of all such amateurs. No formal education provides these gifts. Lack of a mathematical degree separates these “amateurs” from the “professionals,” yet their curiosity and ingenious methods make them true mathematicians.
Information from Doris Schattschneider, “In Praise of Amateurs,” in David A. Klarner (ed.), The Mathematical Gardner, pp. 140–166, plus Plates I-VIII, Wadsworth, Belmont, CA, 1981.
M. C. Escher and Tilings
The Dutch artist M. C. Escher (1898–1972) was inspired by the great variety of decoration in tilings in the Alhambra, a 14th-century palace built during the last years of Islamic dominance in Spain. He devoted much of his career of making prints to creating tilings with tiles in the shapes of living beings. Those prints of interlocking animals and people have inspired awe and wonder all over the world. Figures 20.10 through 20.13 on pages 837–840 illustrate a few of his drawings and finished works. Like Marjorie Rice, he too developed his own mathematical notation for the different kinds of patterns for the tilings.
For more about Escher, see Spotlight 20.3.

Maurits Escher 20.3
20.3
Maurits Escher (1898–1972) was a Dutch graphic artist who specialized in lithograph and woodcut prints. Some of the images in his work were inspired by the landscapes and architecture that he observed while living and traveling in Italy early in his career.
Other works of his—particularly those involving tilings—were stimulated by a visit to the Alhambra, a 14th-century castle in Granada, Spain, built by Moors (Muslims from North Africa). The walls and floors of the Alhambra are tiled in various patterns, including strip patterns and wallpaper patterns. Escher took such patterns and changed their periodic geometric shapes into similarly periodic images of plants and animals.
His prints involving tilings came to the attention of mathematicians at the International Congress of Mathematicians in Amsterdam in 1954. Thereafter, he interacted with mathematicians, with a fruitful crossfertilization of ideas.
Escher is also known for his prints of versions of impossible figures, including one (the Penrose triangle) inspired by the father of Sir Roger Penrose.