20.5 20.4 Using Translations Plus Half-Turns
If the tiling is to allow half-turns, then in order to match up the tiles, some of the figures will appear “upside down.” The part of the boundary of a right-side-up figure has to match the corresponding part of itself in an upside-down position. For that to happen, that part of the boundary must be centrosymmetric: symmetric about the midpoint, that is, unaltered by a 180° rotation around that midpoint. The key to some of Escher’s more sophisticated monohedral designs, and the fundamental principle behind some further easy recipes for making Escher-like tilings, is the Conway Criterion, formulated by John H. Conway (b. 1937) of Princeton University.
Conway Criterion RULE
A tile can tile the plane by translations plus half-turns (including possibly by translations alone) if there are six consecutive points on the boundary (some of which may coincide, but at least three of which are distinct)—call them A, B, C, D, E, and F—such that
- the boundary part from A to B is congruent by translation to the boundary part from E to D, and
- each of the boundary parts BC, CD, EF, and FA is centrosymmetric.
The first condition means that we can match up those two boundary parts exactly, curve for curve, angle for angle. The second condition means that each of the remaining boundary parts is brought back into itself by a half-turn around its center. The second condition is automatically fulfilled if the boundary part in question is a straight-line segment.
The tiles for Figures 20.15 and 20.16 are shown in outline form in Figure 20.17, together with points marked to show how the tiles fulfill the Conway Criterion.
Figure 20.15 shows that Escher sketched tiny circles exactly where we have red dots in Figure 20.17a.



Mathematicians do not know whether the Conway Criterion completely characterizes tiles that can tile by translations and half-turns. Tiles that fulfill the Conway Criterion can tile by translations and half-turns, but there might be tiles that tile that way but do not satisfy the criterion—however, nobody knows of any.
(The Conway Criterion does completely characterize tiles that produce the wallpaper pattern p2 of Spotlight 19.9 on page 797: Any tile that satisfies the criterion can be used to make a p2 pattern, and any tile that can produce that pattern must satisfy the criterion.)
We have considered tilings that tile by translations alone or by translations plus half-turns. You may have noticed differences among the figures, in the following ways:
- In Figures 20.10 and 20.14, all the birds and all the horseheads face the same way, and none are upside down. What if we wanted to allow some of them to be upside down?
- In Figures 20.15 and 20.16, although there are upside-down camels and seahorses, all the right-side-up ones face the same way and all the upside-down ones face the opposite way. What if we wanted to allow both kinds to face both ways?
- In Figure 20.11, there are no upside-down horsemen, but the dark horsemen face left, while the light horsemen face right. The two kinds of horsemen are mirror images of each other; but we avoided letting the tile occur in mirror- image reflections of itself by building the mirroring into the tile itself. However, we noted in Figure 20.12 that a single horseman could be a tile by itself if we allow mirror-image reflections.
In addition to the Translation Criterion and the Conway Criterion, there are several other sufficient criteria for a tile to produce a tiling, depending on what operations we allow on the tile: translations, mirror reflections, glide reflections (illustrated in Figure 19.9, page 792), or rotations by various angles , or . (We have already considered rotations; they are half-turns in the Conway Criterion.) We can’t consider them all here or show the extent to which Escher used them; but in the Suggested Readings and Suggested Websites sections at the end of the chapter, we point to relevant sources and explanations. There is a simple way to implement the Conway Criterion to make Escher-like tilings by starting from any triangle or any quadrilateral. We illustrate this creative process in the following examples.
EXAMPLE 4 Tiling Using a Triangle
Tiling Using a Triangle
How can you make an Escher-like tiling by starting from a triangle?
Modify half of one side of the triangle, then rotate that modified half side around the midpoint of the side to extend the modification to the rest of the side, thereby making the new side centrosymmetric. Then you can do the same to the second and third sides (Figure 20.18).
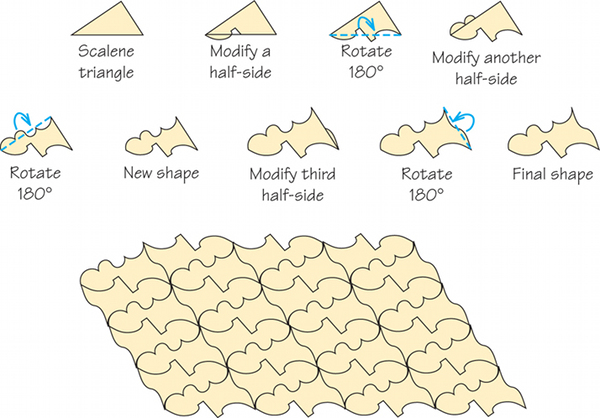
Self Check 4
Start from a triangle and design your own Escher-like tiling.
- Answers will vary.
EXAMPLE 5 Tiling Using a Quadrilateral
Tiling Using a Quadrilateral
How can you make an Escher-like tiling by starting from an arbitrary quadrilateral?
For the quadrilateral, use the same process as in Example 4, modifying some or all of the four sides—as many as you wish (Figure 20.19).

Self Check 5
Start from a quadrilateral and design your own Escher-like tiling.
- Answers will vary.Page 857
The approach of Example 5 will work with some of the sides of some pentagons and hexagons that tile. Because not all sides can be modified, there is less freedom for designing tiles, so it is more difficult to make the resulting tiles resemble intended figures. Figure 20.20 shows the constraints for one kind of tiling by pentagons.

Check the Suggested Websites at the end of this chapter to access a demonstration of all 14 known pentagon tilings and see how much they can be varied in appearance. At another website listed there, you can look at art created by Marjorie Rice from her pentagon tilings.
Sketches in Escher’s notebook indicate how he designed many of his prints. For the bird tiling of Figure 20.10, the single bird below the tiling shows that he modified the sides of a square. For the horsemen tiling of Figure 20.11a on page 838, the sketches in Figure 20.11b show that a pair of horsemen occupy the modified sides of a par-hexagon. We redrew the two fundamental figures more clearly in Figure 20.12 on page 839. (The horsemen tiling also has a glide- reflection symmetry, taking a leftward-facing light horseman to a rightward- facing dark horseman; but we have not discussed criteria for producing a tiling with such a symmetry.)
As can be seen in faint lines in Figure 20.15 (page 841), Escher used a parallelogram as a base for the camel tiling. For the seahorse tiling of Figure 20.16 (page 841), Escher used a triangle base. He treated the triangle in Figure 20.17b (page 842) as a quadrilateral in which two adjacent sides ( and ) happen to continue on in a straight line.
Periodic Tilings PROCEDURE
All the patterns that we have exhibited and discussed so far have been periodic tilings. If we transfer a periodic tiling to a transparency, it is possible to slide the transparency a certain distance in some direction, without rotating it, until the transparency exactly matches the tiling everywhere. We can also achieve the same result by moving the transparency in some second direction (possibly vertically) by a certain (possibly different) distance.
In a periodic tiling, you can identify a fundamental region—a tile, or a block of tiles—with which you can cover the plane by translations, rotations, mirror reflections, and/or glide reflections. For example, in Figure 20.10 (page 837), a single bird forms a fundamental region. In Figure 20.15 (page 841), two adjacent camels, one right side up and one upside down, form a fundamental region. In the terminology of Chapter 19, the periodic tilings are those that are preserved under translations in more than two directions.