20.6 20.5 Nonperiodic Tilings
In Figure 20.3a (page 830), the second row from the bottom is offset one-half of a unit to the right from the bottom row, the third row from the bottom is offset one-third of a unit farther, and so forth. Because whatever the value of n, the sum 12+13+14+⋯+1n never adds up to exactly a whole number, there is no direction (horizontal, vertical, or diagonal) in which we can move the entire tiling and have it coincide exactly with itself.
Nonperiodic Tiling DEFINITION
A nonperiodic tiling is a tiling that cannot be made to coincide with itself by any translation in any direction.
EXAMPLE 6 A Nonperiodic Tiling Through Randomness
A Nonperiodic Tiling Through Randomness
How can you use chance to make a tiling?
Consider the usual edge-to-edge square tiling. For each square, flip a coin. Depending on the result, divide the square into two right triangles by adding either a rising or a falling diagonal (see Figure 20.3b on page 830). Because what happens in each individual square is unconnected to what happens in the rest of the tiling, this random tiling by right triangles has almost no chance of being periodic.
We are not much interested in the arbitrary “random” tilings that can result from a process such as the one described in Example 6. We are much more interested in tilings that are nonperiodic but nevertheless show some kind of order and symmetry.
Penrose Tilings
For all known cases, if a single tile can be used to make a nonperiodic tiling of the plane, then it also can be used to make a periodic tiling. It is still an open question whether this property is true for any shape of tile whatever. Curiously, the answer is known for the corresponding question in three dimensions: In 1993, Conway discovered a single convex polyhedron that tiles space nonperiodically but cannot be used to make a periodic tiling.
For a long time, mathematicians also tended to believe the more general assertion that if you can construct a nonperiodic tiling with a set of one or more tiles, you can construct a periodic tiling from the same tiles. In 1964, however, a set of tiles was found that permits only nonperiodic tiling. It contains 20,000 different shapes! Over the next several years, smaller sets were discovered with the same property, with as few as 100 shapes. But it was still amazing when Sir Roger Penrose (b. 1931), a mathematical physicist at Oxford, announced in 1975 that he had found a set that tiles only nonperiodically—consisting of just two tiles! (See Figure 20.21 and Spotlight 20.4.)
Sir Roger Penrose 20.4
20.4
Sir Roger Penrose, a professor at the University of Oxford, received a doctorate in mathematics but has been seriously interested in physics for many years. He demonstrated mathematically that the collapse of a black hole is “completely general and unstoppable.” He discovered what are now called Penrose tiles in 1974, which were based on an earlier six-tile scheme of his. He has explored the relationship between artificial intelligence and human consciousness, and his more recent endeavor has to do with the development of conformal cyclic cosmology to explain the construction of the universe.
He was “totally fascinated” when he saw Maurits Escher’s exhibit at the International Congress of Mathematicians in 1954. Subsequently, Penrose and his father produced a picture of an impossible staircase, while quite independently Escher did the same in his lithograph Belvedere. Escher followed up with other works of the same nature, as well as a water color Ghosts showing a non-isohedral tiling inspired by Penrose.

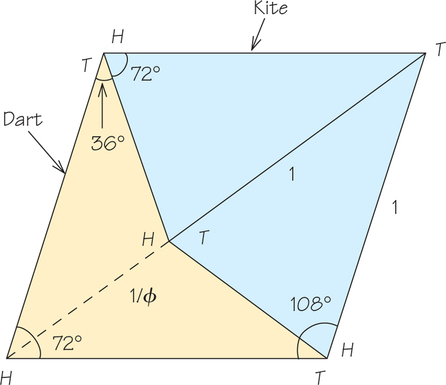
These tiles, together known as Penrose pieces, were named individually by Conway as “darts” and “kites.” One of each can be cut from a single rhombus. A rhombus is a quadrilateral with four equal sides and equal opposite interior angles; it’s like a “leaning” square (see Figure 20.21). The particular rhombus from which the Penrose tiles are constructed has interior angles of 72° and . If we cut the longer diagonal in two pieces so that the longer piece is the golden ratio, or times as long as the shorter (see Chapter 19, page 783), and connect the dividing point to the remaining corners, we split the rhombus into a dart and a kite (Figure 20.21).
Label the front and back vertices of the dart with (for head) and its two wing tips with (for tail), and do the reverse for the kite. Then the rule for fitting the pieces together is that only vertices with the same letter may meet: Heads must go to heads, tails must go to tails. Thus, the rules don’t allow for the pieces to fit together as a rhombus (which would permit them to tile periodically).
A nicer-looking method of enforcing the rules, proposed by Conway, is to draw circular arcs of different colors on the pieces and require that adjacent edges must join arcs of the same color. The result is the pretty patterns of Figure 20.22. In fact, Conway thinks of the darts as children, each with two hands. The rule for fitting the pieces together is that children are required to hold hands. Penrose patterns become dancing circles of children.
Penrose also devised another pair of pieces, a thick rhombus and a thin rhombus, with accompanying matching rules that also force them to tile only nonperiodically; Figure 20.23 shows them used in a tiling.


Figure 20.24 shows a modification of the Penrose pieces into two bird shapes. Figure 20.25 shows a coloring of a Penrose tiling in which no two adjacent pieces have the same color.


Quasiperiodic Tilings
We show that tilings with Penrose’s pieces (1) must be nonperiodic, but nonetheless (2) possess unexpected symmetry. We will say that they are quasiperiodic, a term that we explain carefully later.
Conway invented methods, inflation and deflation,, to make bigger and smaller versions of Penrose patterns. Inflation turns any Penrose pattern into a different Penrose pattern with larger darts and kites, by systematically cutting each dart in half and attaching its halves instead either to a pair of kites, to make a new larger kite, or to a single kite, to make a new larger dart (see Figure 20.26).
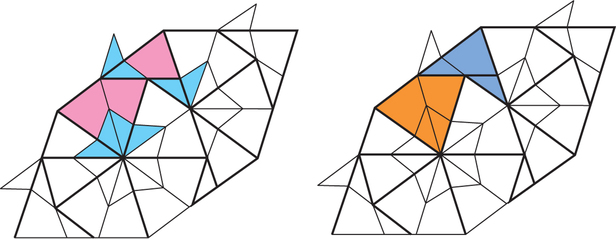
Inflation is handy for showing that any Penrose pattern must be nonperiodic. We offer a proof by contradiction. Suppose (contrary to what we want to establish) that some Penrose pattern is periodic; that is, it has translation symmetry in some direction. Let be the distance along the translation direction to the first repetition. Performing inflation does the same thing to each repetition, so the inflated pattern must still have translation symmetry at the same distance along the translation direction.
Keep performing inflation, time after time, until the darts and kites are so large that they are more than across. The pattern, as we have just argued, must still have translation symmetry at a distance —but it can’t, because there’s no repetition inside a single tile!
We reach a contradiction. So what’s wrong? Our initial supposition, that the pattern was periodic in the first place, must be wrong. We conclude that all Penrose tilings are nonperiodic.
Penrose Tilings Are Nonperiodic THEOREM
Any tiling using Penrose’s pieces (darts and kites) and his rules for fitting them together must be nonperiodic.
In Chapter 19, we explored our intuitions of symmetry in terms of balance, similarity, and repetition. Patterns made with the Penrose pieces certainly involve repetition, but it is the balance in the arrangement that we seek. What balance can there be in a nonperiodic pattern? It turns out that some Penrose patterns have a single line of reflection. But most surprising of all is that every Penrose pattern has a kind of fivefold rotational symmetry.
EXAMPLE 7 How Can a Penrose Pattern Have Fivefold Symmetry?
How Can a Penrose Pattern Have Fivefold Symmetry?
Fivefold symmetry is impossible for regular tilings: How could a Penrose pattern have such symmetry?
Look again at Figure 20.21 on page 846, which shows how to split a rhombus into the Penrose dart and kite pieces. Except in the recess of the dart and the matching part of the kite, each of the internal angles of the kite and of the dart is either 72° or 36°.
Now, 72° goes into 360° 5 times, and 36° goes into 360° 10 times. If we recall that it is the interior angles that matter in arranging polygons around a point, we see why it might be possible for a Penrose pattern to have fivefold or tenfold rotational symmetry.
A Penrose pattern with tenfold rotational symmetry is impossible, but there are exactly two Penrose patterns that tile the entire plane and have fivefold rotational symmetry about one particular point. We show finite parts of these patterns in Figure 20.27. For each pattern, the center of rotational symmetry is at the center of the figure, surrounded by either five darts or five kites.
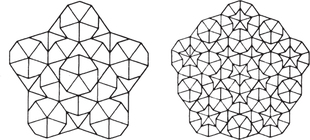
In any other Penrose pattern, the pattern as a whole does not have fivefold rotational symmetry. However, what is surprising is that even so, the pattern must have arbitrarily large finite regions with fivefold rotational symmetry. You can see fivefold symmetry in the larger and larger regions of Figure 20.23 (page 847) that are enclosed by yellow lines. In Conway’s metaphor, whenever a chain of children (the fatter rhombus shapes in the figure) closes, the region inside has fivefold symmetry.
Penrose patterns have another remarkable feature. Despite their being nonperiodic, all Penrose patterns are somewhat alike, in the following sense.
Penrose Inside of Penrose THEOREM
The subpattern of any finite region in one Penrose pattern is contained somewhere inside every other Penrose pattern. In fact, any subpattern occurs infinitely many times in every Penrose pattern.
The nonperiodicity of Penrose tilings found a surprising application in 1997— to bathroom tissue. Quilted bathroom tissue is embossed with a pattern to keep the layers together (Figure 20.28). If the pattern is regular, then the multiple layers on the roll can produce lumpy ridges and grooves. Using a nonrepeating Penrose pattern averts the lumpiness. However, the company used Penrose’s copyrighted design without his permission, and Penrose sued for breach of copyright. They reached a settlement out of court.
Penrose tilings have found decorative use, not only in floor tilings as in Spotlight 20.2 on page 836, but also most notably on a grander scale in the new Transbay Transit Center in downtown San Francisco.
Penrose tilings are quasiperiodic, or somewhere between periodic and random.

Quasiperiodic Tiling DEFINITION
A tiling is quasiperiodic if it exhibits local periodicity under some transformations: You can translate or rotate it so that a finite number of tiles coincide perfectly, yet the entire tiling does not. We say that such a tiling is “locally” periodic but not “globally” periodic.
Musical Sequences
Looking at interpretations of a concept in other dimensions, or a problem in other sizes, is characteristic of the outlook of mathematicians in their search for patterns.
Although the quasiperiodic feature of Penrose tilings may seem apparent from examining them, we can make the idea clearer by considering tilings—in particular, quasiperiodic tilings—in just one dimension instead of in the plane of two dimensions. (Shortly we will also see what such tilings can be in three dimensions.)
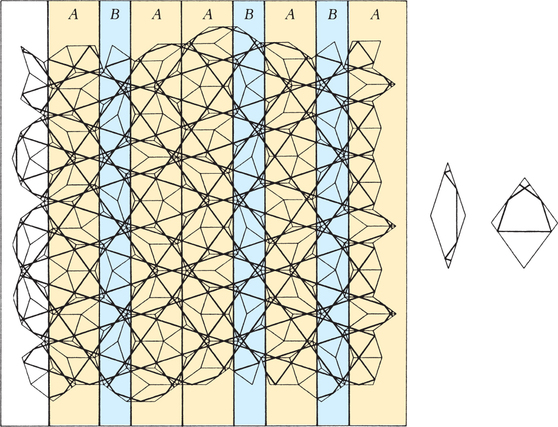
The motivation for such a consideration came from Robert Ammann (1946–1994), who introduced lines onto the two rhombic Penrose pieces (used in Figure 20.23 on page 847) that are now known as Ammann bars. (For more about Robert Ammann, see Spotlight 20.5.)
In any Penrose tiling, these bars line up into five sets of parallel lines, each set rotated 72° from the next, forming a pentagonal grid (see Figure 20.29). The distance between two adjacent parallel bars is one of only two values, either or .
We can think of the pattern of s and s in the Ammann bars of Figure 20.29 as representing a tiling of a line by line segments (the tiles) of lengths and .
Exercise 43 (page 862) asks you to use your imagination to determine the monohedral tilings of the line, as well as periodic tilings with tiles of two different lengths. Exercises 49–62 (pages 863–864) define inflation and deflation operations on tilings of the line, show just what relationship between the lengths and is necessary for a quasiperiodic tiling, and make connections to the Fibonacci sequence and golden ratio of Chapter 19.
Mathematics and Autism 20.5
20.5
In 1975, Martin Gardner wrote in his “Mathematical Games” column in Scientific American about Penrose’s discovery of a set of tiles that do not tile the plane periodically, but do tile it nonperiodically. Gardner did not show any tilings because Penrose was waiting for a patent.
In response to that column, Gardner received a letter from Robert Ammann, who wrote, “I am also interested in nonperiodic tiling, and have discovered both a set of two polygons which tile the plane only nonperiodically and a set of four solids which fill space only nonperiodically.” Ammann included pictures: He had independently discovered Penrose tilings and generalized them to three dimensions.
Ammann went on to do the following:
- Find five more sets of planar tilings
- Discover the general organizing principle behind what are now known as Ammann bars (the one-dimensional analogue of Penrose tilings, which we discuss later and in the exercises)
- Make many other contributions to the theory of nonperiodic tiling (including being the first to find a three-dimensional analogue)
No one in the tiling community knew who Ammann was. He described himself as “an amateur doodler,” and he declined all invitations to meetings and conferences.
In 1987, Marjorie Senechal, a geometer at Smith College, finally succeeded in tracking him down, arranging for him to meet Penrose, Donald Coxeter, and John Conway, and even getting Ammann to speak at two conferences.
After Ammann’s early death from a heart attack in 1994, Senechal learned more about his life. At age three, he was precociously brilliant. At age four, he stopped talking and withdrew into his own world. He struggled through childhood and adolescence, “off the charts intellectually but impossible emotionally.” During the years of his tiling discoveries, he was living in a motel and supporting himself by sorting mail in a post office. His mother said that the mathematical meetings were the high point of his life: “No one else reached out to him.”
Perhaps we should draw the moral that it is important to encourage talent, mathematical or otherwise, wherever we find it, and to welcome into our community all able contributors.
The Mysterious Mr. Ammann, Media Highlights section of the College Mathematics Journal 36(2) (March 2005): 167–168. © 2005 Mathematical Association of America. All Rights Reserved.
Here, we pursue mathematical thinking and ask what kind of patterns there can be in the Ammann bars, as sequences of s and s.
EXAMPLE 8 Musical Sequences
Musical Sequences
What about the order in which the s and s occur, as we move from left to right in Figure 20.29? Is there any pattern to that?
From the limited part of the pattern that we can observe, we see the sequence as
You might think from the figure that the pattern continues repeating the group indefinitely. But such is not the case. The sequence of intervals between Ammann bars is nonperiodic: It cannot be produced by repeating any finite group of symbols. We can think of it as a one-dimensional analogue of a Penrose tiling. The notation is reminiscent of the melody pattern of songs: Many popular songs follow the pattern , with the first and the last sections having the same melody but the middle section being different. Consequently, a sequence of intervals between Ammann bars is known as a musical sequence.
There are some rules that musical sequences follow. Two s can never be next to each other, nor can we have three As in a row (see Exercises 54 and 55 on page 863). Just as any finite part of any Penrose tiling occurs infinitely often in any other Penrose tiling, any finite part of any musical sequence appears infinitely often in any other one. The order of the symbols is neither periodic nor random, but between the two—quasiperiodic.
Self Check 6
If we had looked at a smaller part of the pattern of Ammann bars, we would have seen and possibly conjectured that the pattern continues by repeating over and over. What are the possibilities for the next three bars if they are not to be and there cannot be three s in a row or two s in a row?
- The eight possibilities for three symbols in a row are , , , , , , , and . (Notice how they can all be listed systematically in terms of alphabetical order.) is not possible (three s in a row), and neither are , , or (two s in a row). is also eliminated because it cannot follow (three s in a row). That leaves , , and ; in a musical sequence, it is that, in fact, occurs after .
The ratio of darts to kites in an infinite Penrose tiling, or of s to s in a musical sequence, is exactly the golden ratio, approximately 1.618, as you can show in Exercise 62 on page 864). So if you are going to play with sets of Penrose pieces to see what kinds of patterns you can create, you will need about 1.6 times as many darts as kites.
As pointed out by geometers Marjorie Senechal (Louise Wolff Kahn Professor Emerita in Mathematics and History of Science and Technology, Smith College) and Jean Taylor (Professor Emerita, Rutgers University; Visiting Scholar, the Courant Institute of Mathematical Sciences, New York University), Penrose tilings have three important properties:
- Nonperiodic: They are constructed according to rules that force nonperiodicity.
- Self-similar: They can be obtained from a substitution process (inflation and deflation) that features self-similarity at different scales (like the fractals in Chapter 19).
- Quasiperiodic: They are quasiperiodic, in the sense that we have defined.
These properties are somewhat independent, meaning that a tiling may have just one or two of them without having all three; however, all three are required for a Penrose tiling.
Quasicrystals and Barlow’s Law
Although Penrose’s discovery was a big hit among geometers and in recreational mathematics circles in the mid-1970s, few people thought that his work might have practical significance. In the early 1980s, some mathematicians even generalized Penrose tilings to three dimensions, using solid polyhedra to fill space nonperiodically. Like the two-dimensional Penrose patterns, these have orderly fivefold symmetry but are nonperiodic.
Yet in 1982, scientists at the U.S. National Bureau of Standards discovered unexpected fivefold symmetry while looking for new ultrastrong alloys of aluminum (mixtures of aluminum with other metals).
Manganese doesn’t ordinarily alloy with aluminum, but the experimenters were able to produce small crystals of alloy by cooling mixtures of the two metals at a rate of millions of degrees per second. Following routine procedures, chemist Daniel Shechtman began a series of tests to determine the atomic structure of the special crystals. But there was nothing routine about what he found: The atomic structures of the manganese-aluminum crystals were so startling that it took Shechtman three years to convince his colleagues they were real.
Why did he encounter such resistance? His patterns—and the crystals that produced them—defied one of the fundamental laws of crystallography. Like our discovery that the plane cannot be tiled by regular pentagons, Barlow’s law, also called the crystallographic restriction, says that since the atomic structure of a crystal must be periodic, it can have only rotational symmetries that are twofold, threefold, fourfold, or sixfold. If there were a center of fivefold symmetry, many such centers would have to exist. Barlow proved this impossible.
Peter Barlow (1776–1862) argued by contradiction, the same approach that we saw earlier in Conway’s proof that Penrose patterns are not periodic. Suppose (contrary to what we intend to show) that there is more than one fivefold rotation center. Let and be two of these that are closest together (see Figure 20.30).
Rotate the pattern of Figure 20.29 by one-fifth of a turn clockwise around , which carries to some point . Because the pattern has fivefold symmetry around , the point , which is the image of the fivefold center , must itself be a fivefold center.
Now use as a center and rotate the pattern by one-fifth of a turn clockwise, which carries to some point . As we just argued in the case of , must also be a fivefold center. But and are closer together than and , which is a contradiction. Hence, our original supposition must be false, and a pattern can have at most one fivefold rotation center (as the patterns in Figure 20.27 on page 849, in fact, do) and so cannot be periodic.
For chemists, crystals are modeled well by periodic three-dimensional tilings; an array of atoms with no symmetry whatsoever would not be considered a crystal. Since Barlow’s law shows that fivefold symmetry is impossible in a periodic tiling, no one suspected until Penrose’s discovery that there could be symmetric nonperiodic tilings, or, until Shechtman’s alloys, that real atoms could arrange themselves in such a way.
Shechtman’s alloys, since they are not periodic, are not crystals, though in other respects they do resemble crystals. It is scientifically more fruitful to extend the concept of crystals to include them than to rule them out, so the term crystal now officially encompasses both traditional periodic crystals as well as atomic structures that are not periodic but ordered in some way. The generalized kind of crystals are now known as quasicrystals (see Spotlight 20.6).
Once again, as so often happens in history, pure mathematical research anticipated scientific applications. Penrose’s discovery, once just a delightful piece of recreational mathematics, has prompted a major reexamination of the theory of crystals. Barlow’s law is not refuted, since it applies only to periodic crystals, not to quasicrystals.
Quasicrystals 20.6
20.6
In 1984, working at the University of Pennsylvania, Paul Steinhardt and Don Levine did a computer simulation of what a three-dimensional Penrose pattern would be like. They decided to call such structures quasicrystals. Later that fall, their chemist colleague Daniel Shechtman showed that quasicrystals really exist by synthesizing some. He produced images of an alloy of aluminum and manganese that were amazingly similar to images from the computer simulations. In short order, sevenfold, ninefold, and other symmetries were also shown to occur in real materials.
In 1991, Sergei Burkov showed that quasiperiodic tilings can be made using only a single kind of 10-sided tile, provided the tiles are allowed to overlap. With overlaps, the resulting patterns are no longer tilings. They are called coverages. In late 1998, scientists presented electron microscope photos that demonstrated that atoms really can form such coverages.
The current theory is that quasicrystals are packings of copies of a single type of atom cluster, with each cluster sharing atoms with its neighbors; that is, each cluster overlaps nearby clusters. The clusters form a quasiperiodic pattern that maximizes their density, thereby minimizing the energy of the atoms involved.

The irregular atomic structure of quasicrystals results in the following:
- Low surface energy, making them suitable as coatings for nonstick cookware (a French firm has produced a line of such pots)
- Low friction, desirable in shavers and scalpels
- Quick absorption of heat, useful as an ingredient in the plastic powder used in 3D printers
In 2007, Steinhardt and Peter J. Lu announced the possible discovery of what appeared, to them, to be fragments of decagonal and Penrose tilings in medieval Islamic architecture in Iran; but other scientists have disputed their conclusion.
In 2009, naturally occurring quasicrystals were discovered for the first time in a remote area of Russia, in what appears to be the remains of a meteorite that was formed at the beginning of the solar system.
In 2011, Daniel Shechtman was awarded the Nobel Prize in Chemistry for his discovery of quasicrystals.
