22.4 22.3 Conventional Loans
A common situation that you are likely to encounter is a loan—for a house, a car, or college expenses—that is to be paid back in equal periodic installments. Your payments are said to amortize (pay back) the loan. In these so-called conventional loans, each payment pays the current interest and also repays part of the principal. As the principal is reduced, there is less interest owed, so less of each payment goes to the interest and more toward paying off the principal.
We remind you of the savings formula from Chapter 21 (page 884).
Savings Formula RULE
The amount A that is accumulated
- at a nominal annual rate of interest rate r
- with m compounding periods per year (so interest rate i=r/m per compounding period)
- after t years (hence n=mt compounding periods)
- by a uniform deposit d at the end of each compounding period is
A=d[(1+i)n−1i]=d[(1+rm)mt−1rm]
For the loan situation, the “uniform deposit” becomes the monthly payment:
d=the monthly payment, made at the end of each month
EXAMPLE 3 Buying a House
Buying a House
Suppose that you buy a house with a $100,000 loan to be paid off over 30 years in equal monthly installments. Suppose that the interest rate for the loan is 6.00%. How much is your monthly payment?
Imagine changing the setup slightly so that instead of making monthly payments, you are supposed to pay off the entire principal and interest at the end. Meanwhile, you make payments to a savings fund that you’re building up to pay off the loan, and the savings fund earns the same rate of interest that the loan costs. The interest rate of 6.00% on the loan is compounded monthly, so the monthly rate is 0.5%. At the end of 30 years, the principal and interest on the loan would (by the compound interest formula) amount to
$100,000×(1+0.005)12×30≈$602,257.52
On the other hand, saving d each month for 30 years at 6.00% interest compounded monthly, we know from the savings formula that you will accumulate
d[(1+0.005)360−10.005]
To make d just the right amount to pay off the loan exactly, we need to solve the equation
d[(1+0.005)360−10.005]=$100,000 (1+0.005)12×30≈$602,257.52
for d, getting d≈$599.55 as the monthly payment.
Now, $600,000+ is not what you will be paying over the course of the loan of $100,000! It is only an intermediate amount that we come across in calculating your payment. The total of your loan payments will be (“only”) 360×$599.55=$215,838.00— on a loan of just $ 100,000. (Usually, the bank will round up the regular monthly payment to the next nearest cent, with the consequence that the very last payment will be slightly less than the usual monthly payment.)
It is useful to note that for a 30-year mortgage at 6%, the monthly payment is almost exactly 0.6% of the amount of the loan—here, the payment is $599.55 and 0.6% of $100,000 is $600. Hence, for lower interest rates, the monthly payment will be a lower percentage of the amount of the loan, though the relationship is not proportional.
Self Check 3
What is the monthly payment on a 30-year mortgage for $100,000 if the interest rate is 3.5% per year?
- $449.04

Natural and Fractional Exponents
We put the idea behind the calculation in Example 3 into a more general equivalence: Paying off a conventional loan is like saving. You can think of paying off the loan as making payments to a savings account that earns interest at the same rate as the loan. At the end of the loan term, the savings balance will exactly equal the principal and interest on the loan. Let the loan amount be P, the effective interest rate per compounding period be i, the number of compounding periods be n, and the loan payment be d. We equate the principal and interest on the loan (from the compound interest formula) with the savings balance (from the savings formula):
P(1+i)n=d[(1+i)n−1i]
The quantity P is sometimes called the present value of an annuity of n payments of d, each at the end of a compounding period with interest i per period. This terminology is used in the financial mode of some calculators, such as the TI-83.

Solving for One Variable in Terms of Another
Solving the above equation for d requires a little algebra. To make things simpler, let b=(1+i)n, so
Pb=d[b−1i]
Then
d=P[bb−1i]=P[bib−1]
Now divide numerator and denominator by b, getting
d=P[i1−b−1]
Substituting(1+i)n back for b, we get the usual form of the amortization payment formula.
Amortization Payment Formula RULE
A conventional loan amount P
- at a nominal annual rate of interest rate r
- with m compounding periods per year (so interest rate i=r/m per compounding period)
- for t years (hence n=mt compounding periods)
can be paid off by uniform payments at the end of each compounding period in the amount
d=P[i1−(1+i)−n]=P[rm1−(1+rm)−mt]
The spreadsheet function PMT can be used to check your calculations of the payment amount; see Spotlight 21.3 (page 888) for details and examples.
EXAMPLE 4 Repaying Your Student Loan
Repaying Your Student Loan
The standard repayment option for federal direct student loans is repayment over 10 years with a minimum monthly payment of $50 at the end of each month, beginning six months after you graduate, and a minimum monthly payment of $50. For the $5500 student loan of Example 1 (page 910), if you didn’t pay the interest over the 51 months, what will your monthly payments be on the $6502.83 that you will owe at the start of repayment?
With the amortization payment formula, it’s easy to figure out your monthly payment. We have P=$6502.83, monthly interest rate i=rm=0.042912≈0.003575, and n=mt=12×10=120 months for the payback. We find the payment d as
d=P[rm1−(1+rm)−mt]=$6502.83[0.0429121−(1+0.042912)−12×10]≈$66.74
So your monthly payment will be $66.74. (That is for this loan; you may owe still more per month for loans for your other years in college.) Hence, over the lifetime of the loan, you will pay almost 120×$66.74=$8008.80. We say “almost,” because your last payment will differ by a few cents. Of the total, $8008.80−$6502.83=$1505.97 is interest during the 10-year payback period, plus the $ 1002.83 interest accrued during the deferment and grace periods (calculated in Example 1), for a total of $2508.80 in interest, on an original loan principal of $5500.
In fact, the amount you receive is reduced by an origination fee of 1.073% of the loan amount, or 0.0173×$5500=$95.15; so altogether, you will pay almost 50% as much in interest and fees as the original principal. If you were to stretch your payments over more years (permissible in some circumstances), an even greater proportion would be interest.
You can check these amounts, and those for your own loans, at studentloans.gov/ myDirectLoan/mobile/repayment/repaymentEstimator.action and (with more options and details) at www.finaid.org/calculators/loandiscountanalyzer.phtml.
Self Check 4
Suppose that you graduate with the average amount of student loans to repay, $25,000. What would your monthly payment be if the interest rate on all the loans is 4.29% and the repayment term is the standard 10 years?
- $261.03
EXAMPLE 5 Buying a Car
Buying a Car
You decide to buy a new Wheelmobile car. After a down payment, you need to finance (borrow) an additional $12,000. After you compare interest rates offered by the car dealership, local banks, and your credit union, the lowest monthly payment you can find is for an 84-month loan at 5.9% from the credit union, compounded monthly. What is your monthly payment?
We have P=$12,000, monthly interest rate i=0.059/12≈0.00491667, and n=84. Using the amortization payment formula, we have
d=P[rm1−(1+rm)−mt]=$12,000[0.004916671−(1+0.00491667)−84]≈$174.73
How much interest do you pay? You make payments totaling 84×$174.73=$14,677.32, so the interest is $14,677.32−$12,000=$2,677.32.
If you had bought a Plushmobile instead, with $24,000 to finance, you would have borrowed twice as much, and your monthly payment would have been twice as much.
Self Check 5
What would be your monthly payment on the $12,000 loan, and the total interest paid over the term of the loan, if you got a 60-month loan instead, at the advertised rate of 2.99%?
- $215.57 payment; $934.20 interest
Suppose that you want to buy a car, and you know how much you want to afford for a monthly payment and how long a loan term you would agree to. How much car can you afford? We turn the the amortization payment formula around to solve for P instead of for d:
P=d[1−(1+i)−ni]
EXAMPLE 6 How Much Car Can You Afford?
How Much Car Can You Afford?
Suppose that you feel comfortable with a monthly car payment of $200, you don’t want to pay on the car for more than four years, and you can get financing at 1.99%. How large a loan can you get?
P=d[1−(1+i)−ni]=$200[1−(1+.019912)−48.019912]≈$9221
We have not taken into account the costs of insurance, registration, parking, gasoline, or tolls.
Self Check 6
Suppose that you can afford $250 per month for the car payment (apart from insurance, gas, etc.), you can get a 0% car loan, and you are willing to pay over 7 years. How much car can you afford? (Careful! The amortization payment formula does not apply. Why not?)
- $21,000
A car loan is often for 48 or 60 months; but when you buy a home, you usually borrow a great deal more money and pay it off over a much longer period. The usual term for a home mortgage is 30 years.
EXAMPLE 7 A 30-Year Mortgage on a Median-Priced Home
A 30-Year Mortgage on a Median-Priced Home
Suppose that you are a family with the U.S. median household income of about $53,000 and you want to buy a median-priced home for $205,000, with a 30-year fixed-rate, federally insured mortgage at 3.25% (the data are for the beginning of 2015). Recall that the median (discussed in Section 5.4, pages 196-200) means that half are below and half are above. Suppose that you can make a down payment of only $7000 (just above the minimum of 3.5% required), plus pay closing costs of about $4000. Can you afford such a home?
Mortgage lenders have “affordability” guidelines that suggest that a family cannot afford to spend more than 31% of its monthly income on housing. Thus, by these guidelines, you can afford 0.31×$53,000/12≈$1370 per month.
What is the monthly payment on the loan? The principal is P=$205,000−$7000=$198,000, the monthly interest rate is i=0.0325/12≈0.00270833, and n=360 months. The amortization payment formula gives a monthly payment of
d=P[rm1−(1+rm)−mt]=$198,000[0.0325121−(1+0.032512)−12×30]≈$862
Well, that sounds good. Unfortunately, there is more to the mortgage than just the amount needed to amortize the loan. Your payment will also have to cover real estate taxes, mortgage insurance, and homeowner’s insurance on the property. On a $198,000 home, these may add $500 or more to the monthly payment, which will then total about $1362.
It’s really close! So, the median household may just barely be able to afford the median-priced home (depending on the area of the country), even while interest rates I remain at record lows.
A payment on an amortized loan includes both the current interest and a portion toward repaying the principal. You are “building equity” in a house as you pay off the mortgage.
Equity DEFINITION
Equity is the amount of principal of a loan that has been repaid.
The equity is the sum of the payments made minus the part that went to interest.
EXAMPLE 8 Home Equity
Home Equity
My wife’s parents sold their house in rural Minnesota to move to the town where we live. They had bought their house in 1980 with a 30-year mortgage for $100,000 at an 8% interest rate. After 22 years, how much equity did they have in the house—that is, how much of the principal had been repaid? And how much did they still owe on the house?

What may shock you (and disappointed them) is that when they sold their house in May 2002—after 269 months of payments, almost exactly three-quarters of the 30 years of the mortgage—they had only $50,000 in equity (hence, they still owed $50,000 on the house) but had already paid $147,000 in interest. Three-quarters of their payments had gone to interest.
We can use the amortization payment formula to determine just how much equity they had after 269 months of payments, but first we need to Í determine their monthly payment. We see P=$100,000, n=360 months, and i=0.0812 monthly interest, getting d=$733.76.
Now we use the formula again, this time “in reverse.” Knowing i and d, we find out how much of the loan would have been paid off by the remaining 360−269=91 payments of $733.76:
P=d[1−(1+i)−ni]=$733.76[1−(1+0.0812)−910.0812]≈$49,940
This is how much my parents-in-law had yet to pay, so their equity was $100,000−$49,940=$50,060. (The above formula would not apply if they had made larger or additional payments.)
Self Check 7
Is it true for any mortgage that after three-quarters of the term of the loan, only half of the loan will be paid off?
- No. For example, if the loan is at 0%, then three- quarters of it will be paid off after three-quarters of the term.
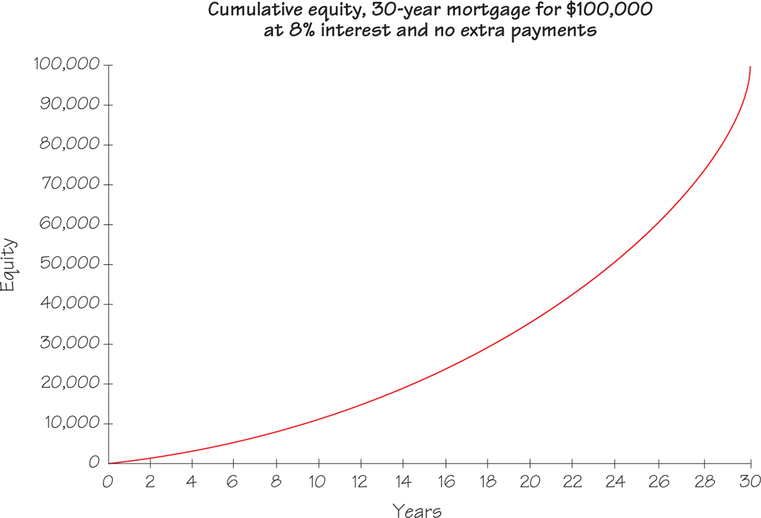
Figure 22.1 and Table 22.1 show that equity builds up very slowly at first but rapidly later. (The values shown do not take into account any increase or decrease in the value of the house itself, the effect of inflation, or the effect of making higher monthly payments or other extra payments.) In fact, the amount of principal in a payment grows by a factor of (1+i) from one payment to the next, so the equity at any point is the sum of a geometric series (discussed in Section 21.5, pages 882-887) whose common ratio is (1+i).
| End of Year | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 | 25 | 30 |
| Equity ($ × 103) | 3 | 6 | 9 | 13 | 16 | 37 | 64 | 99 | 143 | 200 |
When you buy a home, you have several options:
- A conventional 30-year mortgage
- A conventional 15-year mortgage
- An adjustable-rate mortgage (ARM) for either length of time but with an interest rate that can vary
You might expect the payment on a 15-year mortgage to be double that of a 30-year mortgage. On the contrary, the payment is only 55% more (for a 4% mortgage) to 26% more (for a 9% mortgage). This range includes the prevailing mortgage rates over the past 20 years. Moreover, over the course of a $200,000 mortgage at 5%, you would pay $187,000 in interest over 30 years but only $85,000 over 15 years. At 9%, the interest totals are $380,000 versus $166,000.
(Some financial counselors advise taking a 30-year mortgage and making extra payments when you can afford them, rather than incurring the higher payment obligation of a 15-year loan, on which, if you encounter tight personal financial circumstances, you might not be able to make the payments.)
In Spotlight 22.2, we discuss what we did in our own circumstances and mention other options.
What We Did with Our House, and What Else You Could Do 22.2
22.2
We bought our house in 1992. We were offered a choice between a 30-year fixed-rate mortgage at 8.375% and a 30-year ARM at 6.875% whose rate could be raised (or lowered) by up to 2% every year. When we asked, we were also quoted slightly lower rates for corresponding 15-year mortgages.
We were planning to stay in the house much longer than the median of 5 years, and we were concerned that inflation might force the ARM considerably higher. Also, we did not want the obligation of the higher payments of a 15-year mortgage, in case our circumstances changed (such as through job loss or death). Some loans provide for penalties for paying off the loan early, but in our case (thanks to state law), there was no penalty for making extra payments (if we could afford them).
We chose the 8.375% fixed-rate 30-year mortgage (and made some extra payments). People in other circumstances, or with a different tolerance for risk, would no doubt have decided otherwise. Had we been sure then that interest rates would not go higher in the 1990s, we would have gone for the ARM. But hindsight is always better than foresight. Homeowners with mortgage interest rates such as ours later refinanced at much lower prevailing rates, near 5% for a fixed-rate 30-year mortgage.
Currently, about one-third of borrowers take ARMs rather than fixed-rate mortgages. Newer mortgage “products” include interest-only mortgages and shared appreciation mortgages (SAMs). With an interest-only ARM, payments are (just slightly) lower than for a conventional 30-year mortgage, but you accumulate no equity (at least, not by paying off the loan; the market value of the house may rise). After five to seven years, you start also paying off the principal—which means that your payments go up then. In some such loans, the interest rate—and your pay- ments—fluctuate as frequently as every month.
In a SAM, interest payments are lower or nonexistent, but the lender receives a portion of any appreciation (rise in value) when the house is sold. In a nationally reported instance in 2003, a single mother received a no-interest SAM loan to finance the $30,000 down payment on a $223,000 house in Pleasanton, California, through the city’s affordable housing program. Four years later, she sold the house for $385,000, and the “affordable housing” lenders got 60% of the $162,000 appreciation, or $97,000. She herself realized $65,000 (minus the cost of the sale) but complained bitterly, saying that she would have been better off to have put the loan on her credit card! Critics have termed SAMs an urban form of sharecropping.
Because very few mortgages are held for the full term, it is useful to compare the status of mortgages after 5 years, the median length of time that Americans remain in a home. Table 22.2 shows the equity after 5 years for a variety of interest rates. For a 30-year mortgage, the equity after 5 years may be less than the cost of selling the home through a realtor, which is normally 6% to 7% of the sale price. Of course, the resale value of the home also may be higher after 5 years.
A mortgage with an interest rate that can vary is called an adjustable-rate mortgage (ARM). Usually such mortgages have a substantially lower interest rate (hence, a lower payment) than a fixed-rate mortgage. The ARM’s interest rate may go up or down with interest rates in the economy. Normally, the rate can be raised or lowered only every year or two, and then by a limited percentage. An ARM may be attractive if you plan to pay off the mortgage after only a few years, or because it allows for lower payments or buying a more expensive home, or because you do not plan to keep the home long (hence, you would be selling before the interest rate could rise substantially).
| Term (years) | Interest Rate | |||||
|---|---|---|---|---|---|---|
| 4% | 5% | 6% | 7% | 8% | 9% | |
| 15 | 54 | 51 | 48 | 45 | 42 | 40 |
| 30 | 19 | 16 | 14 | 12 | 10 | 8 |
Does it pay to buy a house or apartment? Apart from the joys of ownership, you need to take into account the up-front expenses of closing costs (perhaps $3000), plus the back-end expense of selling the house (usually 6% to 7% if through a realtor, so say $12,000). Consulting the table, and imagining that you get a loan at 5%, you might think that you would finally be in the black on your house as an investment after 6 years (and you have had the pleasure of living in it rent-free!).
However, we have not yet taken into account the ongoing expenses of maintenance, repairs, insurance, and real estate taxes (perhaps $5000 to $10,000 per year). Of course, if your house is rising in value by, say, 5% ($10,000) per year or more, it’s a different story. The growth of home ownership, which rose to 73% before the bursting of the housing bubble in 2007, depended on just such a steady rise in value. Renting may be more attractive if you anticipate moving in just a few years; each year, one-sixth of Americans move.
Spotlight 22.3 details the role of mortgage loans in the Great Recession of 2008 and subsequent years.
The Mortgage Crisis 22.3
22.3
Late 2007 saw the development and widening consequences of what has become known as the “mortgage crisis.” To understand what that was, why it took place, and how it will have widespread effects for some time, you need to know what happens when you get a mortgage to buy a house compared with what used to happen.
In the “good” old days, you would go to a local bank (or savings and loan, or credit union). If you proved “creditworthy”—meaning that after careful consideration, the personnel felt that you could repay the loan—the bank would lend you its money, raised from its depositors. The interest rate depended on your credit rating and down payment. You paid back the loan at a fixed rate of interest, usually over 30 years. If interest rates went down, you could refinance the loan at a lower rate by taking out a new loan to pay off the old one; if rates went up, your payments would not rise.
Meanwhile, the value of your house usually went up 5% to 10% per year, your income went up, and your payments stayed the same. (In fact, if you have only 10% equity in your house and it goes up in value 10% in one year, you have made 100% on your investment! This kind of “leveraging” can make real estate investments very profitable—so long as prices keep rising.)
What changed? Efforts to extend home ownership to a wider proportion of the population resulted in banks making more “subprime” loans (loans to people with poorer credit histories who are less likely or able to repay them), with lower down payments but higher rates of interest (because of the greater risk). Some of those loans were “predatory"—lending at high rates of interest to people who could not possibly make the payments.
Certainly, real estate speculation played a role, as did greed. House prices doubled from 2000 to 2006 (the “housing bubble”), but median income adjusted for inflation remained stagnant—and then fell with increasing unemployment, making it increasingly hard to afford houses. Banks countered with ARMs and interest-only mortgages. They also maximized their income with upfront charges (“origination fee” plus “points” paid by the buyer to lower the interest rate); and at the same time, they minimized their risk by immediately “flipping” the mortgages (selling them to bigger banks or other investors, to whom buyers would then make their payments). All these factors led to banks making more loans that were riskier.
What went wrong? Interest rates rose, and people with ARMs saw their payments rise beyond their ability to pay. At the same time, the “pyramid” of housing prices could not continue with the higher mortgage rates, so housing prices fell. When your house becomes “underwater"—worth less than the balance remaining on the mortgage—you might be better off just walking away from it (especially because you build up almost no equity in the first few years of the mortgage). Mortgage defaults lowered the value of investments in bundles of mortgages.

Houses are worth perhaps hundreds of billions of dollars less than a few years ago, and big investment banks still have mortgages on their hands that are worth hundreds of billions of dollars less than they paid for them. That means that for some time to come, banks have less money to lend and can (indeed, must) demand more creditworthy clients and higher rates of interest.
How does all this affect you? Financial institutions have less money to lend for any purpose—buying a home, buying a car, starting a business, etc.—hence the “credit crunch” following the mortgage crisis. We can only hope that the worst will be over before you are in the market for a house, car, or business loan.
Where you won’t see a direct effect is in the Consumer Price Index (CPI) (discussed in Section 19.5, on pages 785-786, and Section 21.6, on pages 891-893), which is based on the rental value of houses, not their prices. If the doubling of housing prices in 2000-2006 had been taken into account, the CPI would have risen by 5% per year rather than 3%.