People use resources. Some resources are renewable, but others are not. In this section, we model depletion of nonrenewable resources. In the next, we treat renewable resources.

951

Gasoline, coal, and natural gas are important examples, while lottery winnings and inheritances could be examples from personal affairs. There is no practical way to recover or reconstitute these resources after use. Some substances, such as aluminum or the sand used to make glass, are potentially recyclable, but to the extent that we do not recycle them, they, too, are nonrenewable.

For a nonrenewable resource, only a fixed supply is available. Even without human population increases, we face dwindling nonrenewable resources. We are interested in this question: How long will the supply E of a resource last?

As long as the rate of use of the resource remains constant, the answer is easy. If we are using units per year and continue using units per year, then the supply will last years.

The expression is called the static reserve.

This kind of calculation is the basis for claims that at the current rate of consumption, U.S. coal reserves will last 250 years, or that the U.S. strategic reserve of gasoline (stored in underground salt domes in the South) will last 60 days.

However, the rate of use of resources tends to increase with population and with a higher standard of living. For example, projections for use of electric power often assume that use will increase by a fixed percentage each year—that is, geometrically or exponentially. This is the simplest situation (apart from constant usage) and one that we can easily model.

Suppose that is the rate of use of the resource in the first year (this year), and that usage increases each year. Then the usage in the second year is

and usage in the third year is

This is just like compound interest. Generalizing, we see that usage in year will be . Total usage over the next five years, for example, will be

This situation should remind you of the accumulation of regular deposits plus interest (see Chapter 21). Here, the usage corresponds to a deposit, and the increasing rate of use corresponds to the annual interest rate. We may think of the situation as making regular withdrawals (with interest) from a fixed supply of the nonrenewable resource. The savings formula gives

In the resource situation, is the accumulated amount of the resource that has been used up at the end of years, and is the initial rate of use.

952

To find out how long the supply will last, we set the supply equal to the cumulative use over years and then determine what has to be. We have

We perform some algebra to isolate the term involving , to get

At this point, to isolate , we have to take the natural logarithm of both sides:

Doing this gives the final expression

which may look complicated but is quite easy to evaluate on a calculator. The expression for is called the exponential reserve.

We must not take such projections as exact predictions. Estimates of supplies of a resource may underestimate how much is available, and previously unknown sources may be discovered or the technology improved to extract previously unavailable supplies. In addition, as supplies dwindle, the economic considerations of supply, demand, and price come into play. We will never completely run out of any resource. It will always be available “at a price.” In fact, climate scientists suggest that if we are to avoid severe global warming, we will have to leave two-thirds of Earth’s oil and gas resources in the ground.

953

We must not take such projections lightly, either, because we are discussing resources that, once used, are gone forever. In any projection, it is very important to examine the assumptions, because small differences in the rate of increase of use can make big differences in the exponential reserve (see Spotlight 23.3).

In our examples so far, we have assumed that the resource is just sitting there, waiting to be used up. For many natural resources, however, we have to find and develop new sources. As doing that becomes more difficult and more costly, at some point the exponentially increasing demand outstrips the ability to meet that demand.

954

Such a situation is modeled well by the logistic model famously applied to oil by M. King Hubbert, director of Shell Oil Company’s research laboratory. Figure 23.5 shows data for cumulative U.S. oil production through 2013, compared with the logistic curve for the ultimate production of gigabarrels (240 billion barrels).

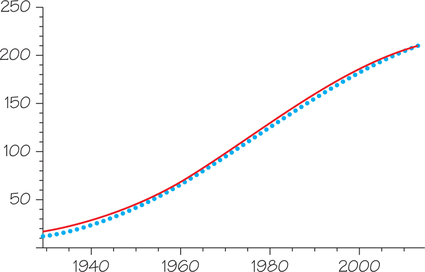
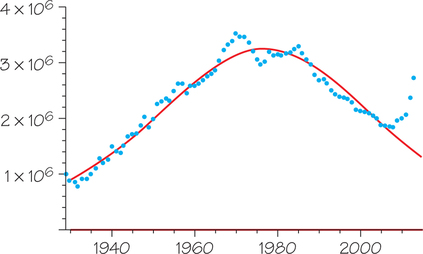
In 1956, Hubbert predicted that U.S. production would peak in the early 1970s (it did) and decline steadily thereafter. It has done that, too, except for a blip from the Prudhoe Bay oilfield in Alaska in the 1980s and now a big bump from fracking (fracturing rock to release oil and natural gas) in the past few years. See Figure 23.6 (the curve is similar to but “heavier in the tails” than the normal distribution curve of Chapter 5).

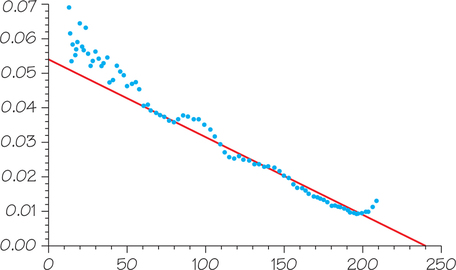
If we rearrange the logistic equation on page 948 by dividing both sides by and doing a little algebra, we get

You can recognize this as the equation of a straight line , where

955

In other words, for a logistic model, if we graph against , we get a straight line. Figure 23.7 shows that the data fit the Hubbert model fairly well until the fracking era. Whether the “bump” from fracking will be just a blip or will add substantially to ultimate production remains to be seen. In any case, we cannot count on being able to find and exploit more and more large quantities of oil.

The world’s oil and gas are running out far faster than most people realize or than their governments are willing to acknowledge (see Exercises 11 and 12). The need for “affordable” fuels will likely soon dominate the political agendas of the entire world, particularly since experts have long predicted that world oil output would peak around 2006. In fact, production leveled off in 2005–2009 at about 85 million barrels per day, or 31 billion barrels per year.