Chapter 2 Exercises
Chapter 2 Exercises
2.1 Hamiltonian Circuits
Question 2.31
1. For the accompanying graphs (a) through (c), write down a Hamiltonian circuit starting at X2.
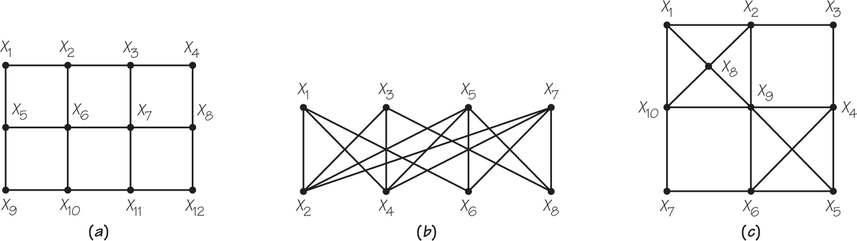
1.
(a) X2X6X7X3X4X8X12X11X10X9X5X1X2
(b) X2X5X8X3X4X7X6X1X2 is one possibility, as is X2X1X4X3X8X5X6X7X2.
(c)X2X8X1X10X7X6X9X5X4X3X2 is one possibility, as is X2X1X8X9X10X7X6X5X4X3X2.
Question 2.32
2. Construct a grid graph with m rows (m at least 3) and n columns (see Figure 2.2b for a 4-by-4 grid graph) that
- has a Hamiltonian circuit.
- does not have a Hamiltonian circuit.
Question 2.33
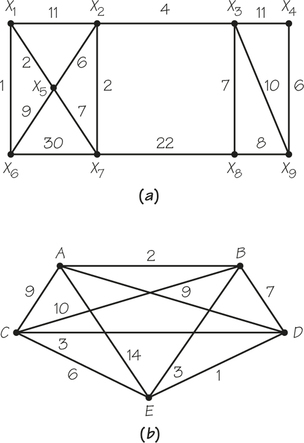
3. For the accompanying graphs (a) through (c), write down, if possible, a Hamiltonian circuit starting at X3.
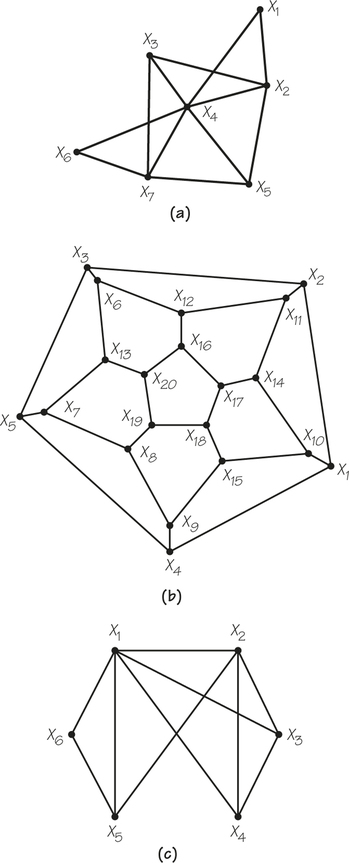
3.
(a) Not possible
(b) A possible answer is X3X2X11X12X6X13X20X16X17X14X10X1X4X9X15X18X19X8X7X5X3
(c) X3X4X2X5X6X1X3
Question 2.34
4.
- For the graph below, write down a Hamiltonian circuit that starts at X3.
- How many vertices are there in the Hamiltonian circuit you found in part (a)?
- How many edges are there in the Hamiltonian circuit you found in part (a)?
- What is the largest number of edges you can remove from the graph shown in part (a) that will still allow one to find a Hamiltonian circuit in the graph after the edges are removed?
Question 2.35
5. For the accompanying graphs (a) through (c), write a Hamiltonian circuit starting at X3.
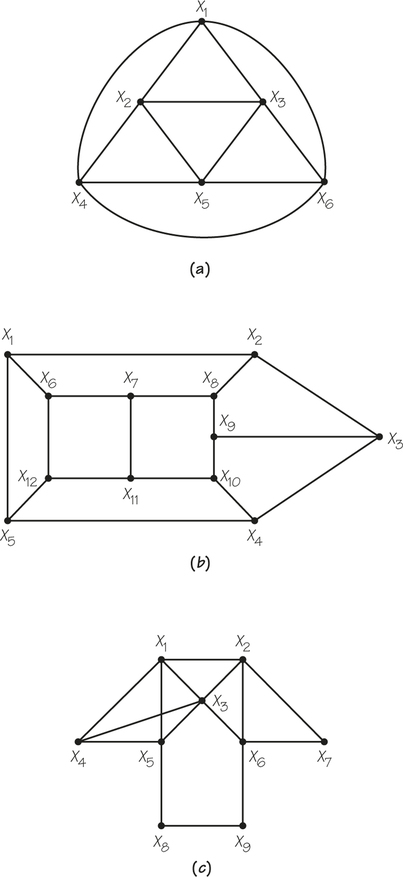
5.
Possible answers include:
(a) Answers will vary. One Hamiltonian circuit is X3X1X2X4X5X6X3.
(b) X3X2X1X6X7X8X9X10X11X12X5X4X3
(c) X3X1X2X7X6X9X8X5X4X3
Question 2.36
6. Refer to the accompanying graph.
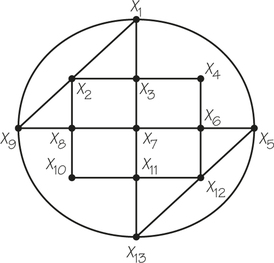
- Find a Hamiltonian circuit starting at X1.
- Determine whether the graph has an Euler circuit starting at X1. (If the graph has an Euler circuit, write it down; if not, give a reason.)
- Explain the difference between a Hamiltonian circuit and an Euler circuit.
Question 2.37
7. If the edge X2X3 is erased from each of the graphs in Exercise 5, does the resulting graph still have a Hamiltonian circuit?
7.
(a) Yes
(b) Yes
(c) Yes
Question 2.38
8.
- If the vertex X6 and the edges attached to X6 are removed from the graphs in Exercise 5, do the new graphs that result still have Hamiltonian circuits?
- If you think of the graphs in Exercise as communications networks, what interpretation might be given to the “removal” of a vertex and the edges attached as described in part (a)?
Question 2.39
9.
- If the edge X6X7 is removed (erased) from each of the graphs in Exercise 1, do the new graphs that result still have Hamiltonian circuits?
- If you think of the graphs in Exercise 1 as communications networks, what interpretation might be given to the “removal” of an edge as described in part (a)?
9.
(a) No for (a); yes for (b); no for (c)
(b) No longer possible to send messages between these two sites
Question 2.40
10.
- Give examples of real-world situations that can be modeled using a graph and for which finding a Hamiltonian circuit in the graph would be of interest.
- For each of the examples you mention in part (a), can you adapt the question about the real-world situation involved so that finding an Eulerian circuit in the same graph would be of interest?
Question 2.41
11. Suppose two Hamiltonian circuits are considered different if the collections of edges that they use are different. How many other Hamiltonian circuits can you find in the graph in Figure 2.1 that are different from the two discussed?
11.
Answers will vary.
Question 2.42
12.
- For each of the following graphs, add wiggly edges to indicate a Hamiltonian circuit.
- Can you see how to construct an infinite family of graphs, each with a Hamiltonian circuit, inspired by how you constructed a Hamiltonian circuit in graph (b) of part (a)?

Question 2.43
13.
- Neither of the following graphs has a Hamiltonian circuit. Is it possible to add a single new edge to these graphs to obtain a new graph that has a Hamiltonian circuit?
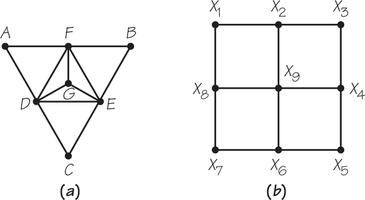
- Find an example of a graph that has no Hamiltonian circuit and will still have no Hamiltonian circuit no matter what single edge is added to it.
- Show that it is possible to add 4 additional edges to the graph diagram in part (b) above so that the resulting new graph will still have no Hamiltonian circuit.
13.
(a) Yes for both.
(b) Answers will vary.
(c) Add edges X2X8,X8X6,X6X4, and X4X2.
Question 2.44
14. Explain why the graph below has no Hamiltonian circuit.
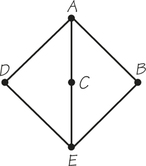
Question 2.45
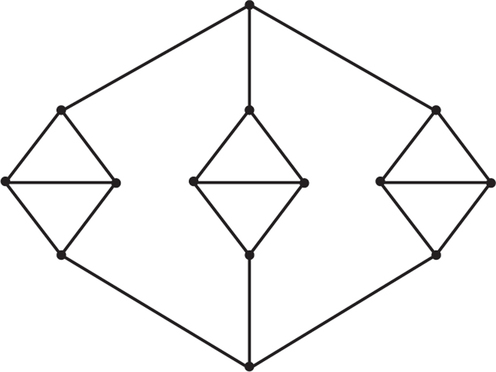
15. Use the graph shown in Exercise 14 to help you construct a connected graph for which every vertex has valence 3 and that does not have a Hamiltonian circuit.
15.
Drawings can vary. Possible renderings include the following:
Question 2.46
![]() 16. Explain why the tour CFECBADBC is not a Hamiltonian circuit for the accompanying graph. Does this graph have a Hamiltonian circuit?
16. Explain why the tour CFECBADBC is not a Hamiltonian circuit for the accompanying graph. Does this graph have a Hamiltonian circuit?
Question 2.47
![]() 17. Do the following graphs have Hamiltonian circuits? If not, can you demonstrate why not?
17. Do the following graphs have Hamiltonian circuits? If not, can you demonstrate why not?
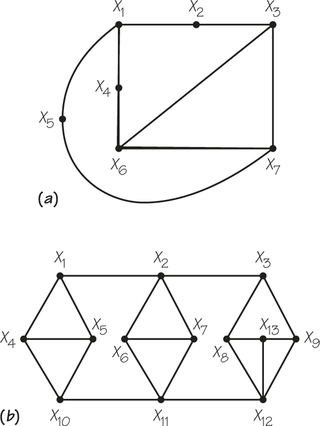
17.
(a) No
(b) No
Question 2.48
18. If an edge from X2 to X5 is added to each graph in Exercise 17, do the new graphs that result have a Hamiltonian circuit?
Question 2.49
19. For each of the accompanying graphs, determine whether there is a Hamiltonian circuit.

19.
(a) Yes
(b) No
(c) No
Question 2.50
![]() 20.
20.
- The graph below is known as a four spokes and three concentric circles graph. What conditions on m and n guarantee that an m spokes and n concentric circles graph has a Hamiltonian circuit? (Assume m≥2, n≥1.)
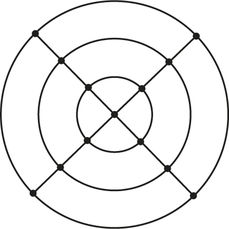
- The graph below is known as a 3×4 grid graph. What conditions on m and n guarantee that an m×n grid graph has a Hamiltonian circuit?
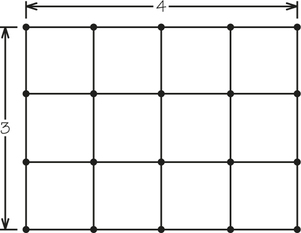
Can you think of a real-world situation in which finding a Hamiltonian circuit in an m×n grid graph would represent a solution to the problem? If an m×n grid graph has no Hamiltonian circuit, can you find a tour that repeats a minimum number of vertices and starts and ends at the same vertex?
Question 2.51
21. A Hamiltonian path in a graph is a tour of the vertices of the graph that visits each vertex once and only once and starts and ends at different vertices.
- For each of the graphs shown in Exercise 17, does the graph have a Hamiltonian path?
- Does each of these graphs have a Hamiltonian path that starts at X1 and ends at X2?
- Describe three real-world situations where finding a Hamiltonian path in a graph would be required.
21.
(a) Yes
(b) No
(c) Answers will vary.
Question 2.52
22. Using the terminology of Exercise 21, draw a graph that has
- a Hamiltonian path but no Hamiltonian circuit.
- an Euler circuit but no Hamiltonian path.
- a Hamiltonian path but no Euler circuit.
- no Hamiltonian path and no Euler circuit.
Question 2.53
23. To practice your understanding of the concepts of Euler circuits and Hamiltonian circuits, determine for the accompanying graphs (a) through (d) whether there is an Euler circuit and/or a Hamiltonian circuit. If so, write it down.
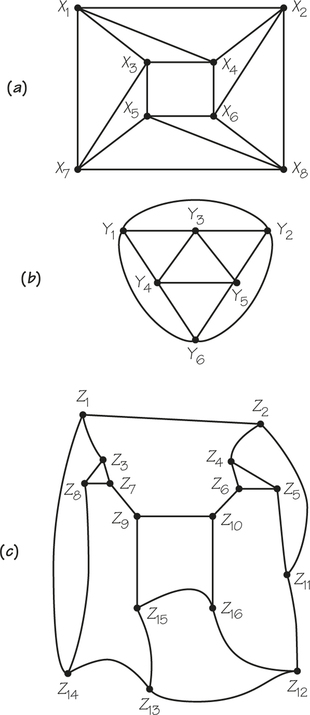
23.
(a) Hamiltonian circuit: yes; Euler circuit: yes; additional answers will vary.
(b) Hamiltonian circuit: yes; Euler circuit: yes
(c) Hamiltonian circuit: yes; Euler circuit: no
(d) Hamiltonian circuit: no; Euler circuit: yes; additional answers will vary.
Question 2.54
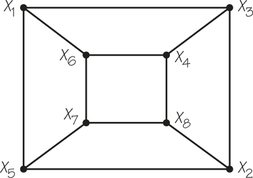
![]() 24.
24.
- The n-dimensional cube is obtained from two copies of an (n−1)-dimensional cube by joining corresponding vertices. (The process is illustrated for the 3-cube and the 4-cube in the following figure.) Can you show that every n-cube has a Hamiltonian circuit? [Hint: Show that if you know how to find a Hamiltonian circuit on an (n−1)-cube, then you can use two copies of this to build a Hamiltonian circuit on an n-cube.]

- Find formulas for the number of vertices and the number of edges of an n-cube.
Question 2.55
25. If an edge is added from the vertex with subscript 3 to the vertex with subscript 6 in each graph in Exercise 23, which of the resulting graphs will have Hamiltonian circuits and which will have Euler circuits?
25.
(a) Hamiltonian circuit: yes; Euler circuit: no
(b) Hamiltonian circuit: yes; Euler circuit: no
(c) Hamiltonian circuit: yes; Euler circuit: no
(d) Hamiltonian circuit: no; Euler circuit: no
Question 2.56
26. Find a family of graphs, none of which has a Hamiltonian circuit but for which adding a single edge to the first graph in the family creates a Hamiltonian circuit, adding two edges to the second graph in the family creates a Hamiltonian circuit, and so forth.
Question 2.57
27. A Hamiltonian path in a graph is a tour of the vertices that visits each vertex once and only once and that starts and ends at different vertices.
- Draw an example of a graph that has no Hamiltonian path and where all the vertices are 3-valent.
- Draw a graph that has no Hamiltonian path but that does have an Euler circuit.
- By analogy with the Hamiltonian path, develop a definition of “Euler path.”
27.
(a) Drawings will vary.
(b) Drawings will vary.
(c) Answers will vary.
Question 2.58
28.
- When going outside on a cold winter day, Jill can choose from four winter coats (three are red), five wool scarves (one is green), four pairs of boots, and three ski hats (two are blue). How many outfits might her friends see her in?
- If Jill always insists on wearing a red coat and a green scarf, how many outfits might her friends see her in?
Question 2.59
29. The notes C, D, E, F, G, A, and B are to be used to form an ordered five-note musical logo. In how many ways can this be done under the following circumstances?
- No note can be repeated.
- Notes can be repeated.
- Notes can be repeated, but all the notes cannot be the same.
29.
(a) 2520
(b) 16,807
(c) 16,800
Question 2.60
30. A lottery game requires a person to select an uppercase or lowercase letter followed by two different odd digits. How many choices can a customer make?
Question 2.61
31.
- In designing a security system for its accounts, a bank asks each customer to choose a five-digit number, all the digits to be distinct and nonzero. How many choices can a customer make?
- A suitcase with a liquid-crystal display allows one to unlock it with a specific combination of three capital letters that are not necessarily different. How many choices would a thief have to go through to be sure that all the possibilities had been tried? How does this compare to a “standard” combination lock?
31.
(a) 15,120
(b) 17,576
Question 2.62
32. To encourage her son to try new things, a mother offers to take him for a dish of ice cream with a topping once a week, for as many weeks as he does not get the same choice as on a previous occasion. If the store offers 12 flavors and 6 toppings, for how many weeks will she have to do this if her son never picks either of the two types of chocolate ice cream or the three types of nut topping that the store carries?
Question 2.63
33. A large corporation has found that it has “outgrown” its current code system for routing interoffice mail. The current system places a code of three ordered, distinct nonzero digits on the mail. The new proposal calls for the use of two ordered capital letters. Does the new system have more code numbers than the old system? If so, how many more locations will the new system enable the company to encode over the current system?
33.
Yes; 172
Question 2.64
34. Repeat Exercise 29a, except that exactly one of the notes in the musical logo must be a sharp and the note chosen to be sharped cannot appear elsewhere (e.g., BCD#AG, where D# denotes D sharp).
Question 2.65
![]() 35.
35.
- In New York State, one type of license plate has three letters followed by three numbers. Suppose the digits from 0, 1, …, 9 can be used, except that all three digits cannot be zero, and that any letter from A to Z (repeats allowed) can be used. How many plates are possible?
- Investigate what schemes for license plates are used in your state and determine how many different plates are possible.
35.
(a) 17,558,424
(b) Answers will vary.
Question 2.66
36. A restaurant offers 6 soups, 10 entrees, and 8 desserts. How many different choices for a meal can a customer make if one selection is made from each category? If 3 of the desserts are pies and the customer will never order pie, how many meals can the customer choose?
Question 2.67
37. In the last several years, heavily populated regions that previously had only one area code have been divided into service areas with more than one area code. What is the largest number of different phone numbers that can be served using one area code? If an area code cannot begin with a zero, how many different area codes are possible?
37.
10,000,000; 900
Question 2.68
38.
- A credit-card company makes it easier for customers to memorize their PIN (personal identification number) by using a four-digit PIN that consists of three different digits selected from 0, 1, 2,… 9, where one of the digits must be a zero, another is a nonzero digit that is repeated, and another is a digit different from these two. How many different PINs of this kind are there?
- How many PINs are possible if there are no restrictions on repeats of the 10 possible digits that can be used?
2.2 Traveling Salesman Problem
2.3 Helping Traveling Salesmen
Question 2.69
39. Draw complete graphs with four, five, and six vertices. How many edges do these graphs have? Can you generalize to n vertices? How many TSP tours would these graphs have? (Tours yielding the same Hamiltonian circuit are considered the same.)
39.
Drawings will vary.; 6, 10, and 15 edges, respectively; n(n−1)2 edges; 3, 12, and 60, respectively
Question 2.70
40. Calculate the values of 5!, 6!, 7!, 8!, 9!, and 10!. Then find the number of TSP tours in the complete graph with eight vertices.
Question 2.71
41. The following table shows the mileage between four cities: Springfield, Ill. (S); Urbana, Ill. (U); Effingham, Ill. (E); and Indianapolis, Ind. (I).
| E | I | S | U | |
| E | — | 147 | 92 | 79 |
| I | 147 | — | 190 | 119 |
| S | 92 | 190 | — | 88 |
| U | 79 | 119 | 88 | — |
- Represent this information by drawing a weighted complete graph on four vertices.
- Use the weighted graph in part (a) to find the cost of the three distinct Hamiltonian circuits in the graph. (List them starting at U.)
- Which circuit gives the minimum cost?
- Would there be any difference in parts (b) and (c) if the starting vertex were at I?
- If one applies the nearest-neighbor method starting at U, what circuit would be obtained? Does the answer change if one applies the nearest-neighbor algorithm starting at S? At E? At I?
- If one applies the sorted-edges method, what circuit would be obtained? Does one get the optimal answer?
41.
(a) Possible drawings include the following:
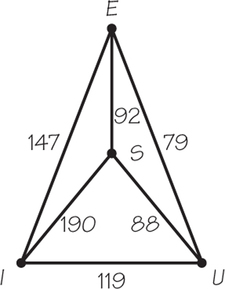
(b) Tour 1: UISEU: 480
Tour 2: USIEU: 504
Tour 3: UIESU: 446
(c) Tour 3
(d) No
(e) Tour 1; yes; yes; no
(f) Tour 2; no
Question 2.72
42. After a party at her house, Francine (F) has agreed to drive Mary (M), Rachel (R), and Constance (C) home. If the times (in minutes) to drive between her friends’ homes are shown below, what route gets Francine back home the quickest?
Question 2.73
43. In Exercise 42, what route would Francine have to follow to get home as quickly as possible, assuming she promised to drive Constance home first?
43.
FCMRF
Question 2.74
44. In Exercise 42, Francine is planning to deliver her friends home and then spend the night at Rachel's house. What would her fastest route be?
Question 2.75
45.
 A religious charity arranges free pickups for donated goods to encourage such donations but would like to keep its pickup costs low. The accompanying diagram shows the estimated amounts of time to get between the charity (H) and the locations of the three pickups scheduled for Wednesday.
A religious charity arranges free pickups for donated goods to encourage such donations but would like to keep its pickup costs low. The accompanying diagram shows the estimated amounts of time to get between the charity (H) and the locations of the three pickups scheduled for Wednesday.
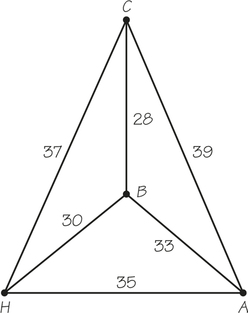
- What route is selected using the nearest-neighbor algorithm starting at H?
- What route is selected using the sorted-edges algorithm?
- Use “brute force” to determine if the solution in either (a) or (b) yields an optimal solution.
45.
(a) HBCAH
(b) HBCAH
(c) The cheapest route costs 132 and coincides with the nearest-neighbor solution from H and the sorted-edges solution.
Question 2.76
46. An organization that delivers meals to the needy elderly must deliver food to three clients and wants to keep down its costs. Typical times to get between its home site H and the clients are given in the accompanying graph.
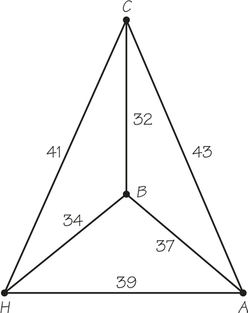
- What route is selected using the nearest-neighbor algorithm starting at H?
- What route is selected using the sorted-edges algorithm?
- Use “brute force” to determine whether the solution in either part (a) or (b) yields an optimal solution.
- Compare the times in the diagrams in this excercise and Exercise 45. How do they differ? Can you state a general result about solving TSPs based on what you notice?
Question 2.77
47. Starting from the location where she moors her boat (M), a fisherwoman wishes to visit three areas—A, B, and C—where she has set fishing nets. If the times (in minutes) between the locales are given in the accompanying figure, what route to visit the three sites and return to the mooring place would be optimal?

47.
MACBM
Question 2.78
48.
- For the two complete graphs that follow, find the costs of the nearest-neighbor tour starting at B and of the tour generated by the sorted-edges algorithm.
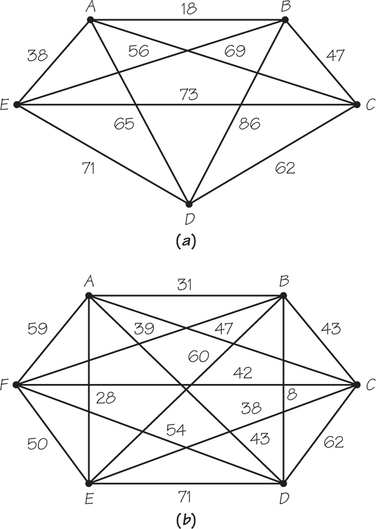
 How many Hamiltonian circuits would have to be examined to find a shortest route for part (a) by the brute force method?
How many Hamiltonian circuits would have to be examined to find a shortest route for part (a) by the brute force method?- Invent an algorithm different from the sorted-edges and nearest-neighbor algorithms that is easy to apply for finding TSP solutions.
Question 2.79
49. An airport limo must take its five passengers from the airport to different downtown hotels. Is this a traveling salesman problem, a Chinese postman problem, or an Euler circuit problem?
49.
A traveling salesman problem
Question 2.80
50. For each of the accompanying graphs with weights, apply the nearest-neighbor method (starting at vertex A) and the sorted-edges method to find (it is hoped) a cheap tour.
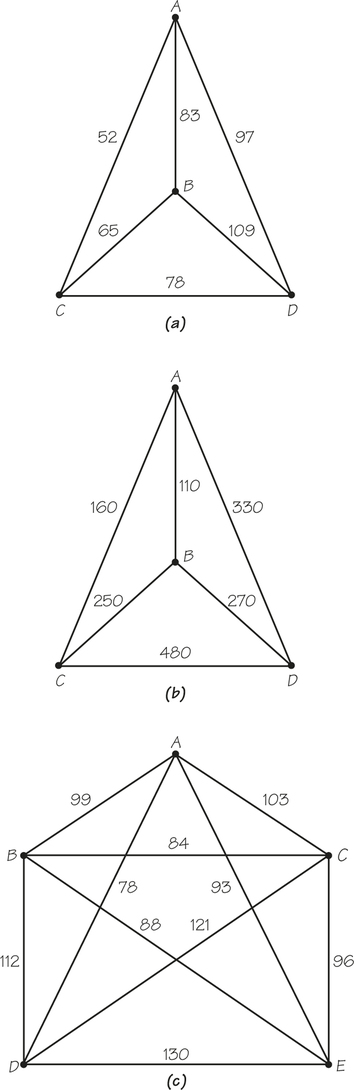
Question 2.81
51. The accompanying figure represents a town where there is a sewer located at each corner (where two or more streets meet). After every thunderstorm, the department of public works wishes to have a truck start at its headquarters (at vertex H) and make an inspection of sewer drains to be sure that leaves are not clogging them. Can a route start and end at H that visits each corner exactly once? (Assume that all the streets are two-way streets.) Does this problem involve finding an Euler circuit or a Hamiltonian circuit?
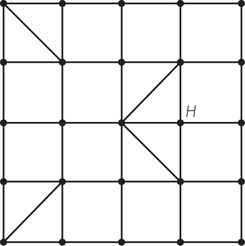
Assume that at equally spaced intervals along the blocks in this graph, there are storm sewers that must be inspected after each thunderstorm to see if they are clogged. Is this a Hamiltonian circuit problem, an Euler circuit problem, or a Chinese postman problem? Find an optimal tour to do this inspection.
51.
Yes; Hamiltonian circuit; Chinese postman problem; answers will vary and require at least 9 reuses of edges.
Question 2.82
52.
- Solve the six-city TSP shown in the diagram using the nearest-neighbor algorithm starting at vertex A and starting at vertex B.
- Apply the sorted-edges method.
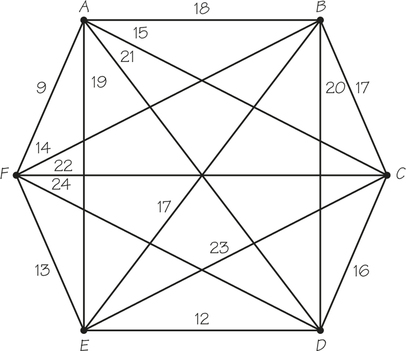
Question 2.83
![]() 53. Construct an example of a complete graph of five vertices, with distinct weights on the edges for which the nearest-neighbor algorithm starting at a particular vertex and the sorted-edges algorithm yield different solutions for the traveling salesman problem. Can you find a five-vertex complete graph with weights on the edges in which the optimal solution, the nearest- neighbor solution, and the sorted-edges algorithm solution are all different?
53. Construct an example of a complete graph of five vertices, with distinct weights on the edges for which the nearest-neighbor algorithm starting at a particular vertex and the sorted-edges algorithm yield different solutions for the traveling salesman problem. Can you find a five-vertex complete graph with weights on the edges in which the optimal solution, the nearest- neighbor solution, and the sorted-edges algorithm solution are all different?
53.
Answers will vary.
Question 2.84
![]() 54. If the brute force method of solving a 20-city TSP is employed, use a calculator to determine how many Hamiltonian circuits must be examined. How long would it take to determine the minimum- cost tour if the cost of tours could be computed at the rate of 1 billion per second? (Convert your answer to years by seeing how many years are equivalent to a billion seconds!)
54. If the brute force method of solving a 20-city TSP is employed, use a calculator to determine how many Hamiltonian circuits must be examined. How long would it take to determine the minimum- cost tour if the cost of tours could be computed at the rate of 1 billion per second? (Convert your answer to years by seeing how many years are equivalent to a billion seconds!)
Question 2.85
55. Suppose one has found an optimal tour for a given 10-city TSP to have weight 4200. Now suppose the weights on the edges of the complete graph are increased by 50. What can you say about the optimal tour and its weight?
55.
The optimal tour is the same but its cost is now 4700.
2.4 Minimum-Cost Spanning Trees
Question 2.86
56. For each graph below, explain why it is or is not a tree.
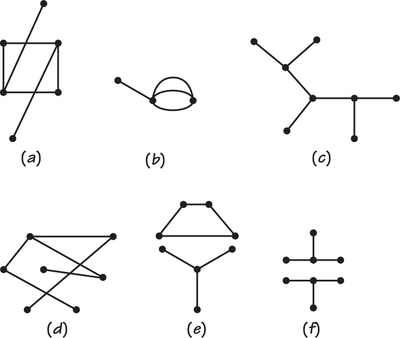
Question 2.87
57. For each of the accompanying diagrams, explain why the wiggly edges are not
- a spanning tree.
- a Hamiltonian circuit.
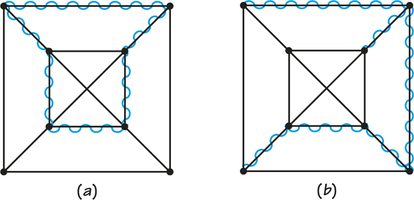
57.
Diagram (a): (a) There is a circuit and wiggled edges do not include all vertices. (b) The circuit does not include all the vertices of the graph.
Diagram (b): (a) The tree does not include all vertices of the graph. (b) Not a circuit
Diagram (c): (a) Not a tree (b) Not a circuit
Diagram (d): (a) Not a tree (b) Not a circuit
Question 2.88
58. Find all the spanning trees in the accompanying graphs.
Question 2.89
59. Use Kruskal's algorithm to find a minimum-cost spanning tree for the following graphs (a), (b), (c), and (d). In each case, what is the cost associated with the tree?
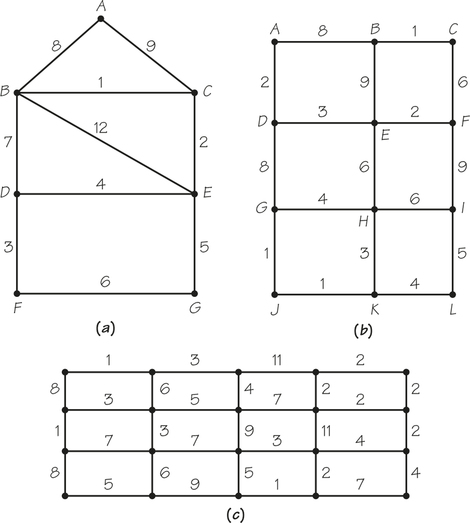
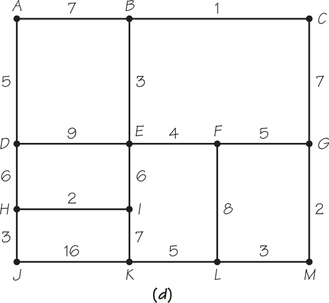
59.
(a) 1, 2, 3, 4, 5, 8; cost is 23.
(b) 1, 1, 1, 2, 2, 3, 3, 4, 5, 6, 6; cost is 34.
(c) 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 5, 5, 6, 7; cost is 60.
(d) 1, 2, 2, 3, 3, 3, 4, 5, 5, 5, 6, 6; cost is 45.
Question 2.90
60. A connected graph G has 14 vertices. How many edges does a spanning tree of G have? How many vertices does a spanning tree of G have? What can one say about the number of edges G has?
Question 2.91
61. A connected graph H has a spanning tree with 26 edges. How many vertices does the spanning tree have? How many vertices does H have? What can one say about the number of edges H has?
61.
H’s spanning tree has 24 vertices; H has 24 vertices. H has at least 23 edges and, if there are no multiple edges, at most (24)(23)/2 edges.
Question 2.92
62. A large company wishes to install a pneumatic tube system that would enable small items to be sent between any of 10 locales, possibly by using relay. If the nonprohibitive costs (in $100) are shown in the accompanying graph model, between which sites should the tube be installed to minimize the total cost?
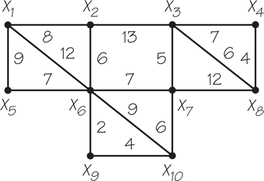
Question 2.93
63. If the weight of each edge in Exercise 60 is increased by 3, will the tree that achieves minimum cost for the new collection of weights be the same as the one that achieves minimum cost for the original set of weights?
63.
Yes
Question 2.94
![]() 64. Give examples of real-world situations that can be modeled using a weighted graph and for which finding a minimum-cost spanning tree for the graph would be of interest.
64. Give examples of real-world situations that can be modeled using a weighted graph and for which finding a minimum-cost spanning tree for the graph would be of interest.
Question 2.95
![]() 65. Can Kruskal’s algorithm be modified to find a maximum-weight spanning tree? Can you think of an application for finding a maximum-weight spanning tree?
65. Can Kruskal’s algorithm be modified to find a maximum-weight spanning tree? Can you think of an application for finding a maximum-weight spanning tree?
65.
Yes; additional answers will vary.
Question 2.96
![]() 66. Find the cost of providing a relay network between the six cities with the largest populations in your home state, using the road distances between the cities as costs. Does it follow that the same solution would be obtained if air distances were used instead?
66. Find the cost of providing a relay network between the six cities with the largest populations in your home state, using the road distances between the cities as costs. Does it follow that the same solution would be obtained if air distances were used instead?
Question 2.97
![]() 67. Would there ever be a reason to find a minimum-cost spanning tree for a weighted graph in which the weights on some of the edges were negative? Would Kruskal’s algorithm still apply?
67. Would there ever be a reason to find a minimum-cost spanning tree for a weighted graph in which the weights on some of the edges were negative? Would Kruskal’s algorithm still apply?
67.
Yes; yes
Question 2.98
![]() 68. Suppose G is a graph such that all the weights on its edges are different numbers. Show that there is a unique minimum-cost spanning tree.
68. Suppose G is a graph such that all the weights on its edges are different numbers. Show that there is a unique minimum-cost spanning tree.
Question 2.99
69. Two spanning trees of a (weighted) graph are considered different if they use different edges. Show that the following graph has different minimum-cost spanning trees, though all these different trees have the same cost.
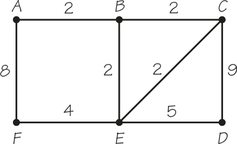
69.
There are three different trees with the same cost.
Question 2.100
70. Let G be a graph with weights assigned to each edge. Consider the following algorithm:
- Pick any vertex V of G.
- Select an edge E with a vertex at V that has a minimum weight. Let the other endpoints of E be W.
- Contract the edge VW so that edge VW disappears and vertices V and W coincide (see the following figures).
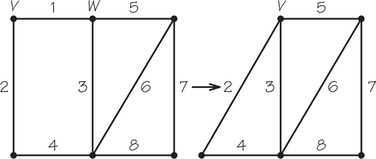
If in the new graph two or more edges join a pair of vertices, delete all but the cheapest. Continue to call the new vertex V.
(d) Repeat steps (b) and (c) until a single point is obtained. The edges selected in the course of this algorithm (called Prim’s algorithm) form a minimum-cost spanning tree. Apply this algorithm to the accompanying graphs.
Question 2.101
71. Determine whether each of the following statement: is true or false for a minimum-cost spanning tree T for a weighted connected graph G:
- T contains a cheapest edge in the graph.
- T cannot contain a most expensive edge in the graph.
- T contains one fewer edge than there are vertices in G.
- There is some vertex in T to which all others are joined by edges.
- There is some vertex in T that has valence 3.
71.
(a) True
(b) False (unless all the edges of the graph have the same weight)
(c) True
(d) False
(e) False
Question 2.102
![]() 72. In the accompanying graphs, the number in the circle for each vertex is the cost of installing equipment at the vertex if relaying must be done at the vertex, while the number on an edge indicates the cost of providing service between the endpoints of the edge.
72. In the accompanying graphs, the number in the circle for each vertex is the cost of installing equipment at the vertex if relaying must be done at the vertex, while the number on an edge indicates the cost of providing service between the endpoints of the edge.
In each case, find the minimum cost (allowing relays) for sending messages between any pair of vertices, taking vertex relay costs into account.
Would your answer be different if vertex relay costs were neglected? (Warning: Kruskal’s algorithm cannot be used to answer the first question. This problem illustrates the value of having an algorithm over relying on “brute force.”)
Question 2.103
73.
- Show that for each edge of graph J, which follows, there is a spanning tree of J that avoids that edge.
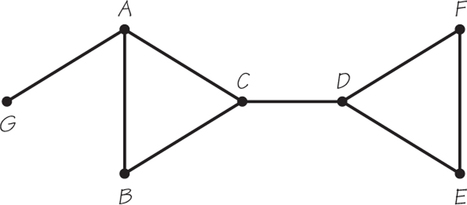
- For each spanning tree that you found in graph J, count the number of vertices and edges. Do you notice any pattern?
- For graph H, which follows, and each edge in the graph, is there a spanning tree that does not include that edge of H?

73.
(a) Answers will vary for each edge.
(b) 5; one less than the number of vertices in the graph
(c) No (CD and AG must be included in any spanning tree.)
Question 2.104
74.
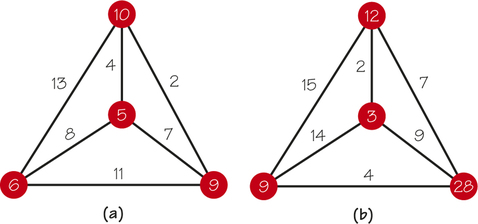
- The table shown gives the “closeness” or distance values between four objects. Construct a four-vertex tree with weights on its edges such that the distances between pairs of vertices of the tree (as measured by the sum of the weights on the path in the tree between these vertices) give rise to this table.
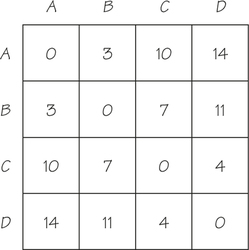
- Produce several real-world contexts that might give rise to the situation described here.
Question 2.105
75. The accompanying figure represents four objects using a tree with weights on the edges. Construct a table with four rows and four columns recording how “close” pairs of vertices in the tree are to each other. To find how close a pair of objects is, add together the weights along the path that joins these two objects.
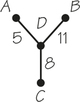
75.
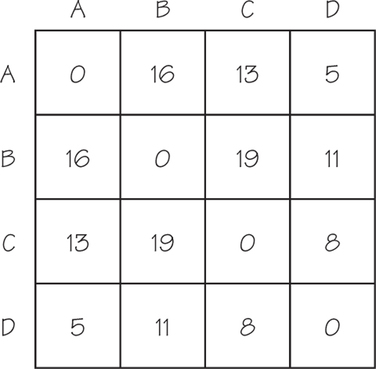
2.5 Critical-Path Analysis
Question 2.106
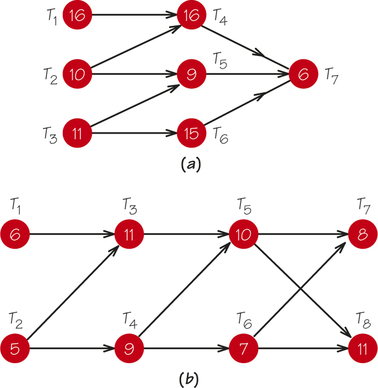
76. Find the earliest completion time and critical paths for the accompanying order-requirement digraphs.
Question 2.107
77. Find the earliest completion time and critical paths for the following order-requirement digraphs.
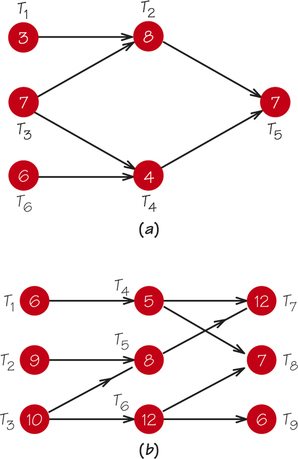
77.
(a) 22; T3T2T5
(b) 30; T3T5T7
Question 2.108
78. Construct an example of an order-requirement digraph with exactly three different critical paths.
Question 2.109
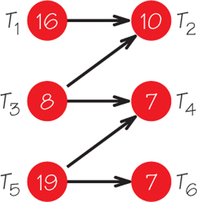
79. In the accompanying order-requirement digraph, determine which tasks, if shortened, would reduce the earliest completion time and which would not. Then find the earliest completion time if task T5 is reduced to time length 7. What is the new critical path?
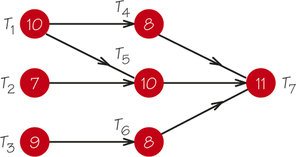
79.
T1, T5, and T7 if shortened would reduce the earliest completion time, while shortening the other tasks will not; 29; T1T4T7.
Question 2.110
80. For the order-requirement digraph in Exercise 79, find the critical path and the task(s) in the critical path whose time, when reduced the least, creates a new critical path.
Question 2.111
81. To build a new addition on a house, the following tasks must be completed:
- Lay foundation.
- Erect sidewalls.
- Erect roof.
- Install plumbing.
- Install electric wiring.
- Lay tile flooring.
- Obtain building permits.
- Put in door connecting new room to existing house.
- Install track lighting on ceiling.
- Install wall air-conditioner.
Construct reasonable time estimates for these tasks and a reasonable order-requirement digraph. What is the fastest time in which these tasks can be completed?
81.
Answers will vary.
Question 2.112
82. At a large toy store, scooters arrive unassembled in boxes. To assemble a scooter, the following tasks must be performed:
| Task 1. | Remove parts from the box. |
| Task 2. | Attach wheels to the footboard. |
| Task 3. | Attach vertical housing. |
| Task 4. | Attach handlebars to vertical housing. |
| Task 5. | Put on reflector tape. |
| Task 6. | Attach bell to handlebars. |
| Task 7. | Attach decals. |
| Task 8. | Attach kickstand. |
| Task 9. | Attach safety instructions to handlebars. |
Give reasonable time estimates for these tasks and construct a reasonable order-requirement digraph. What is the earliest time by which these tasks can be completed?
Question 2.113
83. Construct an order-requirement digraph with six tasks that has three critical paths of length 26.
83.
Drawings can vary. Possible renderings include the following:
Chapter Review
Question 2.114
84. Use the nearest-neighbor method starting at D and the sorted-edges method to find a hopefully short way to deliver packages from the depot at D to the other four sites in the accompanying complete graph.

Question 2.115
85. Mary must choose a new password where the first and last choices are possibly repeated lowercase letters; the second and third positions must be distinct capital letters; the fourth position must be a #, $, or & symbol; and the next three positions are distinct nonzero digits. In how many ways can she choose a password?
85.
The number of passwords can be found by performing the following multiplication: (26)(26)(26)(25)(3)(9)(8)(7).
Question 2.116
86. Does the graph G in Chapter 1, Exercise 71 (page 36), have a Hamiltonian circuit? If so, write one down that starts at H.
Question 2.117
87. Use Kruskal’s algorithm to make cable television available for the sites in the accompanying graph, assuming that video can be relayed. The costs of putting in connections are shown.
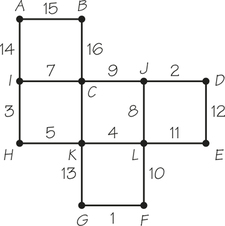
87.
The edges are added to the minimum-cost spanning tree in this order: GF, JD, IH, KL, HK, IC, JL, Fl, LE, AI, AB.