2.6 2.5 Critical-Path Analysis
Mathematics can confirm the obvious in certain situations while showing that our intuition is wrong in other circumstances. Our next group of applications will illustrate this point.
A characteristic of American life is its fast pace. People are interested in getting things done quickly and efficiently. This means that when you take your car in to be repaired before going to work, you want to know for sure that the repairs will be done when you pick up the car. You want the trains and the bus that take you to your doctor’ s appointment to run on time. When you arrive at the doctor’s office, you want a technician to be free to take a blood sample and a throat culture. You want your outpatient appointment for an X-ray at the local hospital to occur on schedule. You want the X-ray to be interpreted quickly and the results reported back to your internist.
Scheduling machines and people is a big part of modern life. It is involved in running a school, a hospital, an airline, or in landing a person on Mars, and modern mathematics plays a big part in solving scheduling problems.
Part of what makes scheduling complicated is that the tasks that make up a job usually cannot be done in a random order. For example, to make Thanksgiving dinner, you must buy and prepare the turkey before putting it in the oven, and you must set the table before serving the food.
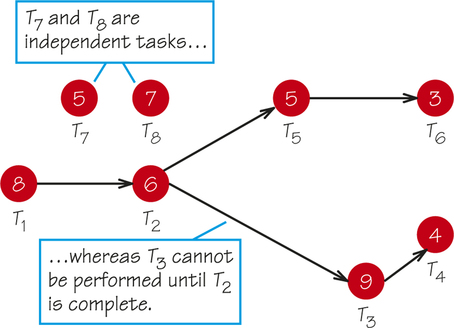
If the tasks cannot be performed in a random order, we can specify the order in an order-requirement digraph. The term digraph is short for “directed graph.” A digraph is a geometrical tool similar to a graph except that each edge has an arrow on it to indicate a direction for that edge. Digraphs can be used to illustrate that traffic on a street must go in one direction or that certain tasks in a job must be completed before other tasks. A typical example of an order-requirement digraph is shown in Figure 2.16. There is a vertex in this digraph for each task. If one task must be done immediately before another, we draw a directed edge, or arrow, from the prerequisite task to the subsequent task. The numbers within the circles representing vertices are the times it takes to complete the tasks. In Figure 2.16, there is no arrow from T1 to T5 because task T2 intervenes. Tasks T7 and T8 are independent of each other. Either task can be performed before the other, and we do not have to take into account priorities for the other tasks to schedule them. There are no directed arrows entering or leaving T7 or T8, and such arrows would force them to be performed in a particular order with respect to the other tasks or to each other. Also, T1, T7, and T8 have no tasks that must precede them. Hence, if there are at least three processors (such as people or machines) available, tasks T1, T7, and T8 can be worked on simultaneously at the start of the job.
Let’s investigate a typical scheduling problem faced by a business.
EXAMPLE 8 Turning a Plane Around
Turning a Plane Around
Consider an airplane that carries both freight and passengers. The plane must have its passengers and freight unloaded and new passengers and cargo loaded before it can take off again. Also, the cabin must be cleaned before departure can occur. Thus, the job of “turning the plane around” requires completion of five tasks:
| Task A | Unload passengers | 13 minutes |
| Task B | Unload cargo | 25 minutes |
| Task C | Clean cabin | 15 minutes |
| Task D | Load new cargo | 22 minutes |
| Task E | Load new passengers | 27 minutes |

The order-requirement digraph for the problem of turning an airplane around is shown in Figure 2.17. The presence or absence of an edge in the order-requirement digraph depends on the analysis made as part of the modeling process for the problem. it seems natural that we need an arrow between task A and task C, because the passengers have to be unloaded before the cabin is cleaned. Other arrows may not seem natural—say, perhaps the arrow from task B (unload the cargo) to task E (load new passengers). This arrow may be due to government rules or union requirements.
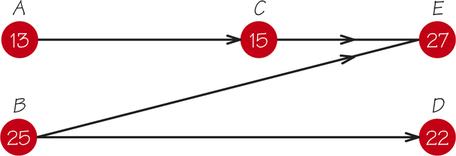
What matters is that the mathematics of solving the problem does not depend on the reason that the order-requirement digraph looks the way that it does. The person solving the problem constructs the order-requirement digraph and then the mathematical techniques we will develop can be applied, regardless of whether or not another business faced with a similar problem might model the problem in a different way by using a different order-requirement digraph. Because we want to find the earliest completion time, it might seem that finding the shortest path in the digraph (path BD with time length 25+22=47) would solve the problem. But this approach shows the danger of ignoring the relationship between the mathematical model (the digraph) and the original problem.
The time required to complete all the tasks, A through E, must be at least as long as the time necessary to do the tasks on any particular path. Consider the path BD, which has length 25+22=47. Recall that here length of a path refers to the sum of the times of the tasks that lie along the path. Because task B must be done before task D can begin, the two tasks B and D cannot be completed before time 47. Hence, even if work on other tasks (such as A, C, and E) proceeds during this period, all the tasks cannot be finished before the tasks on path BD are finished. The same statement is true for every other path in the order-requirement digraph. Thus, the earliest completion time actually corresponds to the length of the longest path. in the airplane example, this earliest completion time is 55(=13+15+27) minutes, corresponding to the path ACE. We call ACE the critical path because the times of the tasks on this path determine the earliest completion time.
Critical Path DEFINITION
A critical path in an order-requirement digraph is a longest path. The length is measured in terms of summing the task times of the tasks making up the path.
Self Check 4
Determine the tasks that make up the critical path in the order-requirement digraph shown in Figure 2.16. What is the earliest completion time for the job made up of this collection of tasks?
- The tasks on the critical path are T1, T2, T3, and T4. The job consisting of all the tasks cannot be completed before time 27.
Note that if none of these tasks could go on simultaneously, the time to complete all the tasks would be 13+25+15+22+27=102 minutes. However, even though some tasks may be performed simultaneously, the fact that the length of the critical path is 55 means that completion of the tasks in less than 55 minutes is not possible. Only by speeding up the times to complete the critical-path tasks themselves can a completion time less than 55 minutes be achieved.
Suppose it were desirable to speed the turnaround of the plane to less than 55 minutes. One way to do this might be to build a second jetway to help unload passengers more quickly. For example, we could unload passengers (task A) in 7 minutes instead of 13. However, reducing task A to 7 minutes does not reduce the completion time by 6 minutes, because in the new digraph (Figure 2.18) ACE is no longer the critical (longest) path. The longest path is now BE, which has a length of 52 minutes. Thus, shortening task A by 6 minutes results in only a 3-minute saving in completion time. This may mean that building a new jetway is uneconomical.
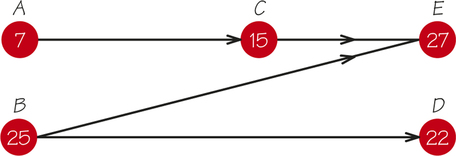
Note also that shortening the time to complete tasks that are not on the original critical path ACE will not shorten the completion time at all. Speeding up tasks on the critical path will shorten completion time of the job only up to the point where a new critical path is created. Also note that a digraph may have more than one longest path.
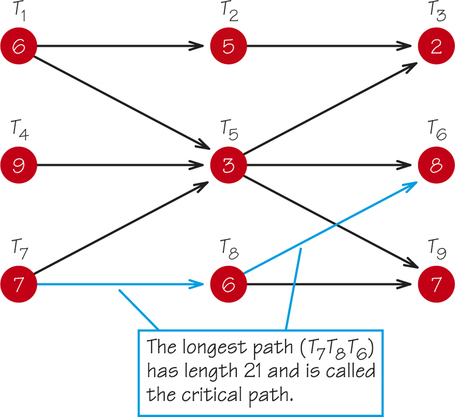
Not all order-requirement digraphs are as simple as the one shown in Figure 2.17. The order-requirement digraph in Figure 2.19 has 12 paths, which can be found by exhaustive search. Examples of such paths are T1T2T3, T1T5T9, T4T5T9, and T7T5T3. (Although we have not discussed them here, fast algorithms for finding longest and shortest paths in graphs are known.) The critical path is T7T8T6 (length 21), and the earliest completion time for all nine tasks is time 21, though the actual completion time may be later than time 21, depending on the resources available to carry out the tasks. Completing the tasks by time 21 depends on having sufficient resources available so that some of the tasks can be worked on simultaneously.
These examples are typical of many scheduling problems that occur in practice (see Spotlight 2.4). Perhaps the most dramatic use of critical-path analysis is in the construction trades. No major new building project is now carried out without a critical-path analysis first being performed to ensure that the proper personnel and materials are available at the right times in order to have the project finished as quickly as possible. Many such problems are too large and complicated to be solved without the aid of computers.
The critical-path method was popularized and came into wider use as a consequence of the Apollo project. This project, which aimed at landing a man on the moon within 10 years of 1960, was one of the most sophisticated projects in planning and scheduling ever attempted. The dramatic success of the project can be attributed partly to the use of critical-path ideas and the related program evaluation and review technique (PERT), which helped keep the project on schedule.
Every Moment Counts in Rigorous Airline Scheduling 2.4
2.4
When people think of airline scheduling, the first thing that comes to mind is how quickly a particular plane can safely reach its destination. But using ground time efficiently is just as important to an airline’s timetable as the time spent in flight. Bill Rodenhizer was the manager of control operations for an airline that provided shuttle service between Boston and New York. He is considered to be an expert on airplane turnaround time, the process by which an airplane is prepared for almost immediate takeoff once it has landed. He tells us how this well-orchestrated effort works:
Scheduling, to the airline, is just about the whole ball game. Everything is scheduled right to the minute. The whole fleet operates on a strict schedule. Each of the departments responsible for turning around an aircraft has an allotted period of time in which to perform its function. Manpower is geared to the amount of ground time scheduled for that aircraft. This would be adjusted during off-weather or bad-weather days or during heavy air-traffic delays.
Most of our aircraft in Boston are scheduled for a 42- to 65-minute ground time. Boston is the end of the line, so it is a “terminating and originating station.” in plain talk, that means almost every aircraft that comes in must be fully unloaded, refueled, serviced, and dispatched within roughly an hour’s time.
This is how the process works: in the larger aircraft, it takes passengers roughly 20 minutes to load and 20 minutes to unload. During this period, we will have completely cleaned the aircraft and unloaded the cargo, and the caterers will have taken care of the food. The ramp service may take 20 to 30 minutes to unload the baggage, mail, and cargo from underneath the plane, and it will take the same amount of time to load it up again. We double-crew those aircraft with heavier weights so that the workload will fit the time it takes passengers to load and unload upstairs.
While this has been going on, the fueler has fueled the aircraft. As to repairs, most major maintenance is done during the midnight shift, when [most of our] several hundred aircraft are inactive. We all work under a very strict time frame.
New security requirements in the wake of the World Trade Center attack (9/11/2001) have increased the difficulty of adhering to timetables in operating shuttle services between East Coast cities such as New York and Boston. This makes it even more important to use analytical tools in keeping operations on schedule.
In Chapter 3, we will see how mathematical ideas drawn from outside of graph theory can be used to gain insight into scheduling problems.