Skills Check
![]() Skills Check
Skills Check
Question 2.1
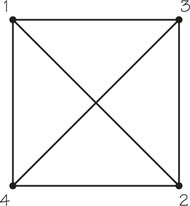
1. Which of the statements below is false for the graph G shown?
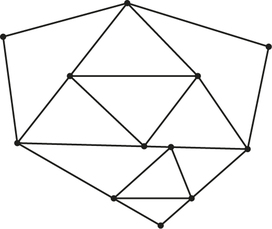
- G has an Euler circuit.
- G has no spanning tree.
- G is not even-valent.
- G has no Hamiltonian circuit.
1.
c
Question 2.2
2. The cost of the nearest-neighbor tour for the accompanying graph, starting at vertex 3, is _____________.
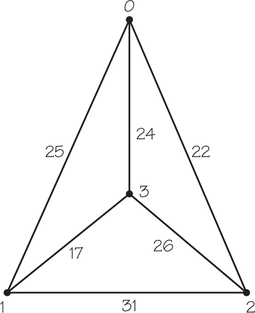
2.
90
Question 2.3
3. The cost associated with the TSP tour 0, 2, 1, 3, 0 in the accompanying graph is
- 48.
- 47.
- −48.
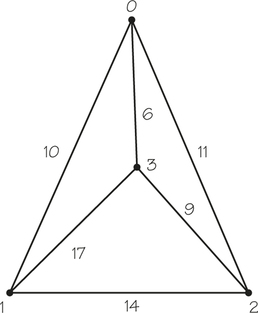
3.
a
Question 2.4
4. The difference between the cost of a nearest-neighbor tour starting at D and the cost of a sorted-edges tour for the accompanying graph is ___________.
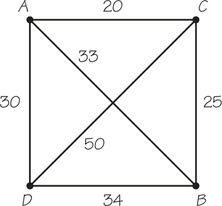
4.
0
Question 2.5
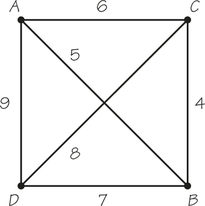
5. The tour 1, 3, 2, 4 is not a Hamiltonian circuit because
- it does not include all of the vertices of the graph.
- it is not a circuit.
- there are other ways to get from 1 to 4 in this graph.
5.
b
Question 2.6
6. The cost of the nearest-neighbor tour (Hamiltonian circuit) that starts at vertex A for the accompanying graph is ________________.
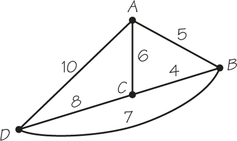
6.
27
Question 2.7
7. The accompanying graph has no Hamiltonian circuit because
- it is even-valent.
- it has an odd number of vertices.
- it is not connected.
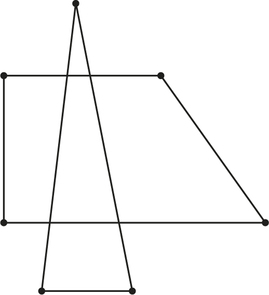
7.
c
Question 2.8
8. The cost of the sorted-edges tour (Hamiltonian circuit) for the accompanying graph is __________________.
8.
26
Question 2.9
9. Which of the following describes a Hamiltonian circuit for the graph below?
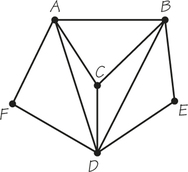
- ABCDFA
- AFDCBE
- ACBEDFA
- ACEBDFA
9.
c
Question 2.10
10. The cost of the nearest-neighbor traveling salesman tour that starts at D for the graph below is __________.
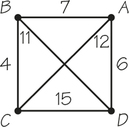
10.
32
Question 2.11
11. Suppose that after a hurricane, a van is dispatched to pick up five nurses at their homes and bring them to work at the local hospital. Which of these techniques is most likely to be useful in solving this problem?
- Finding an Euler circuit in a graph
- Finding a minimum-cost spanning tree in a graph
- Solving a TSP (traveling salesman problem)
11.
c
Question 2.12
12. If a graph has E edges and V vertices as well as a Hamiltonian circuit, then the number of edges in the Hamiltonian circuit is ___________.
12.
V
Question 2.13
13. The following graph has
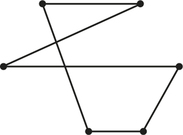
- no Hamiltonian circuit and no Euler circuit.
- an Euler circuit and a Hamiltonian circuit.
- no Hamiltonian circuit, but it has an Euler circuit.
13.
b
Question 2.14
14. The longest-circuit tour of vertices that arises by applying the nearest-neighbor algorithm starting at any of the sites 0, 1, 2, 3 in the graph below has a cost of __________.
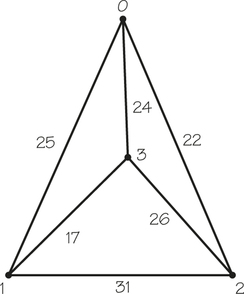
14.
94
Question 2.15
15. When the sorted-edges method and nearest-neighbor method are applied to a complete graph on seven vertices with nonnegative weights,
- both methods always give different answers.
- both methods always give the same answer but that answer may not be optimal.
- neither method may give an optimal answer.
15.
c
Question 2.16
16. The number of different lunches that Jules can design by selecting one of three meats, one of four salads, and one of six vegetables is exactly __________.
16.
72
Question 2.17
17. When the sorted-edges method is applied to the TSP where all the edges have distinct costs, which of the following must be true of the tour S obtained?
- The largest-weight edge cannot be part of tour S.
- The shortest-weight edge must be part of tour S.
- The length of the tour S must be odd.
17.
b
Question 2.18
18. If a three-character password system must begin with a lowercase letter of the English alphabet followed by two decimal digits that cannot be repeated, the number of different possible passwords is ___________.
18.
2340
Question 2.19
19. Paul has packed four ties, three shirts, and two pairs of pants for a trip. How many different outfits can he create if he never wears a tie?
- Fewer than 12
- Between 11 and 25
- More than 30
19.
a
Question 2.20
20. A company is designing a logo with two identical lowercase letters with a single nonzero digit between the letters. A typical possible example would be d3d. The number of such logos is _____________.
20.
234
Question 2.21
21. An ice-cream shop offers 3 types of cones, 20 flavors, and 4 different toppings (crushed peanuts, crushed almonds, chocolate bits, or corn flakes). If a customer is allergic to nuts, how many different choices can she choose from?
- 240
- 120
- 25
21.
b
Question 2.22
22. A minimum-cost spanning tree for the weighted accompanying graph has weight _______ and ________ edges.
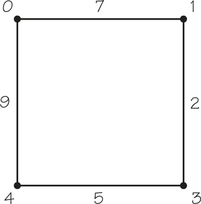
22.
14; 3
Question 2.23
23. Assuming a graph with E edges and V vertices has a minimum-cost spanning tree T, which of the following statements must be true?
- The graph is connected.
- The tree T includes every minimum-cost edge.
- The tree T has exactly V edges.
23.
a
Question 2.24
24. When arranged in increasing order, the weights of the edges in the following graph that are not part of the minimum-cost spanning tree selected when Kruskal’s algorithm is applied are _________, ________, _______.
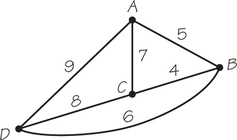
24.
7; 8; 9
Question 2.25
25. The cost of the last edge that Kruskal’s algorithm selects to be part of a minimal-cost spanning tree for the weighted graph below is _________.
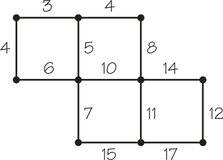
25.
14
Question 2.26
26. Assume that every edge of a graph G has a different cost. If Kruskal’s algorithm is used to find the minimum-cost spanning tree T for graph G, which of the following statements must be true?
- Any other spanning tree for graph G will have more edges than T.
- Any other spanning tree for graph G will have a greater cost than T.
- The edge of graph G having greatest weight is included in T.
26.
b
Question 2.27
27. If a graph contains a circuit, which of the following statements is true?
- The graph must have the same number of vertices as edges.
- The graph cannot be a tree.
- The graph is not connected.
27.
b
Question 2.28
28. The earliest completion time (in minutes) for a job with the following order-requirement digraph is ____________.
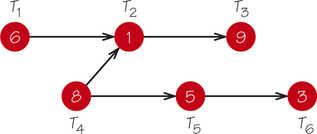
28.
18
Question 2.29
29. Assume a job has an order-requirement digraph with five tasks whose critical path is 25 minutes in length. Based on this information, what can be said about the tasks?
- Each task takes exactly 5 minutes.
- Some task takes 25 minutes.
- The five tasks in total take at least 25 minutes.
29.
c
Question 2.30
30. The length of the critical path in the accompanying order-requirement digraph is ____________ minutes.
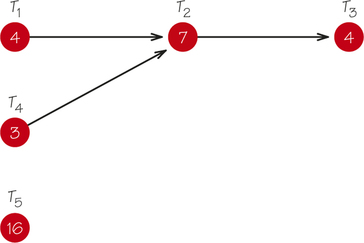
30.
16