Chapter 3 Exercises
Chapter 3 Exercises
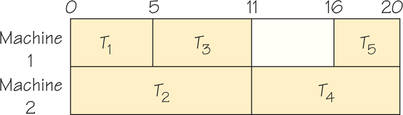
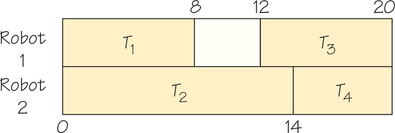
3.1 Scheduling Tasks
3.2 Critical-Path Schedules
Question 3.31
1. You and your two housemates are planning to have a party this Friday night at your apartment. Eight guests are expected, and you plan to serve a small homemade dinner. List the tasks involved in carrying out such a party and the types of processors to be used to carry out the tasks. Can any of the tasks be done simultaneously?
1.
Answers will vary.
Question 3.32
2. Compare and contrast the scheduling problems that arise at a
- fast-food restaurant.
- standard sit-down restaurant.
Question 3.33
3. List as many scheduling situations as you can for these environments:
- Your school
- Bus/train terminal
- Medical center
- Police station
- Bookstore
- 24-hour drug store
- Firehouse
3.
Answers will vary.
Question 3.34
![]() 4. Jane is planning a getaway weekend at a ski resort. She plans to leave work in Manhattan at 1 P.M. and must make her way to a local airport for a 5 P.M. shuttle plane to Boston. She then hopes to get a bus to the nearby resort. Discuss the tasks that Jane must complete to be at the resort by 10 P.M. What are the different types of processors involved in getting these tasks done? Can any of these tasks be done simultaneously?
4. Jane is planning a getaway weekend at a ski resort. She plans to leave work in Manhattan at 1 P.M. and must make her way to a local airport for a 5 P.M. shuttle plane to Boston. She then hopes to get a bus to the nearby resort. Discuss the tasks that Jane must complete to be at the resort by 10 P.M. What are the different types of processors involved in getting these tasks done? Can any of these tasks be done simultaneously?
Question 3.35
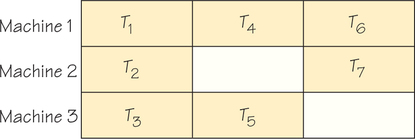
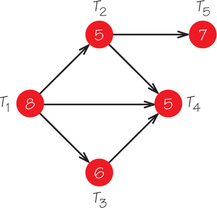
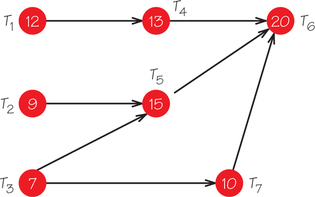
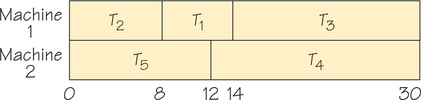
5. Schedule the six tasks of the job indicated in the accompanying order-requirement digraph on one processor, using the list-processing algorithm and the list T1, T2, T3, T4, T5, T6.
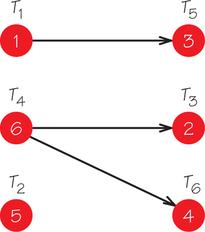
5.
The tasks would be scheduled so that T1 gets done from 0 to 1, T2 from 1 to 6, T4 from 6 to 12, T3 from 12 to 14, T5 from 14 to 17, and T6 from 17 to 21. Even though there is only one machine, the tasks don't appear in the schedule in the order they appear in the list because of restrictions in task order due to the order-requirement digraph.
Question 3.36
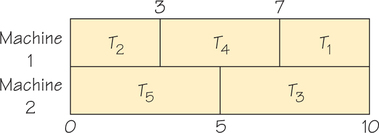
6. Use the list-processing algorithm to solve the scheduling problem in Exercise 5 on two processors.
Question 3.37
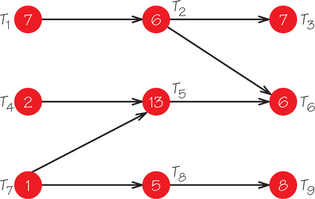
7. Use the list-processing algorithm to schedule the tasks in the accompanying order-requirement digraph on
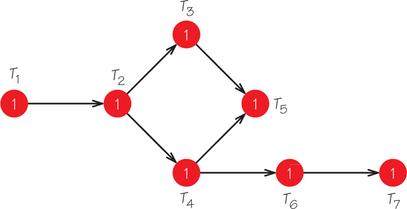
- two processors using the list T1, …, T7.
- two processors using the list T1, T2, T3, T4, T6, T5, T7.
- Is either of the schedules that you obtain optimal?
- Will adding a third processor enable the tasks to be finished earlier?
- Which tasks in this order-requirement digraph can be shortened and not affect the completion time of all the tasks?
7.
(a) Processor 1: T1,T2,T3,T5,T7; Processor 2: Idle 0 to 2, T4,T6, idle 4 to 5
(b) Processor 1: T1,T2,T3,T6,T7; Processor 2: Idle 0 to 2, T4, T5, idle 4 to 5
(c) Yes
(d) No
(e) T3 and T5
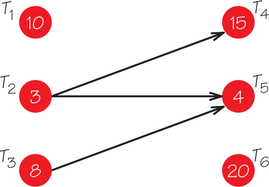
Question 3.38
8. Consider the order-requirement digraph below:
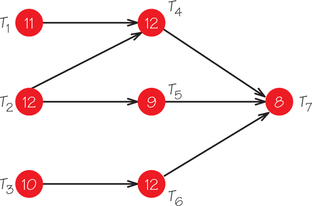
- Find the length of the critical path.
- Schedule these seven tasks on two processors using the list algorithm and the lists:
- T1, T2, T3, T4, T5, T6, T7
- T2, T1, T3, T6, T5, T4, T7
- Does either list lead to a completion time that equals the length of the critical path?
- Show that no list can ever lead to a completion time equal to the length of the critical path (providing the schedule uses two processors).
Question 3.39
9.
- For what value of “?” will the order-requirement digraph have a critical path of length 16?
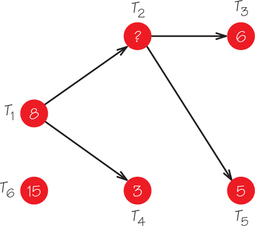
- If the time for T2 is set to the answer in part (a), what is the largest amount of time that T5 can increase so the earliest completion time for the job involving the six tasks is still 16?
9.
(a) 2
(b) 1
Question 3.40
10. For the accompanying order-requirement digraph, answer the following questions.
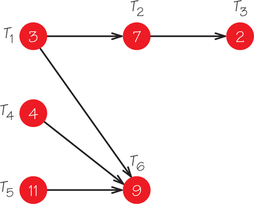
- Find the length of the critical path(s) and which tasks are on the critical path(s).
- Which task(s) (taken one at a time) would not alter the length if the time of that task were to increase by 1 time unit?
- With two processors, can these tasks be scheduled to finish by time 20? If so, what list L would enable you to apply the list-processing algorithm and finish by time 20 on two processors?
Question 3.41
11. An order-requirement digraph has exactly two vertices that have no edges coming into them. Explain why, if there are three processors available, one or more of these processors must be idle some of the time.
11.
The two vertices with no incoming edges correspond to the only tasks that are ready at time 0. These tasks are assigned to different processors at time 0, forcing the third processor to be idle for some period of time.
Question 3.42
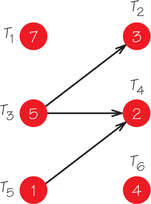
12.
- If the tasks subject to an order-requirement digraph are scheduled on only one machine, explain what different goals one might have in choosing to use different lists to schedule the tasks.
- Find the schedule for the accompanying order- requirement digraph, using the list T1, T2, T3, T4, T5, T6 on one processor.
Question 3.43
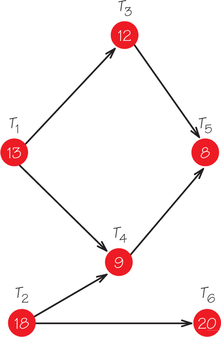
13.
- Use the accompanying order-requirement digraph to schedule the 6 tasks T1, T2, T3, T4, T5, T6 on two processors with the priority lists:
- T1, T2, T3, T4, T5, T6
- T1, T6, T3, T5, T4, T2
- Are either of the schedules produced from these lists optimal? If not, can you find a priority list that will result in an optimal schedule?
- Find the critical path and its length. Explain why no schedule has an earliest completion time equal to the length of the critical path.
13.
(a) (i) Processor 1: T1 from 0 to 13, T3 from 13 to 25, T6 from 25 to 45; Processor 2: T2 from 0 to 18, T4 from 18 to 27, T5 from 27 to 35, idle from 35 to 45 (ii) Processor 1: T1 from 0 to 13, T3 from 13 to 25, T4 from 25 to 34, T5 from 34 to 42; Processor 2: T2 from 0 to 18, T6 from 18 to 38, idle from 38 to 42
(b) Yes
(c) T2,T6, and 38; sum of the task times divided by 2 is 40.
Question 3.44
14.
- Repeat Exercise 13, but interchange the task times of tasks T2 and T6.
- How does the completion time for an optimum schedule for this situation compare with the optimum schedule for Exercise 13?
Question 3.45
15.
- If we add a new directed edge to an order-requirement digraph D, can the critical path in the new order-requirement digraph D′ have longer length?
- If we add a new directed edge to an order-requirement digraph D, can the critical path in the new order- requirement digraph D′ have shorter length?
15.
(a) Yes
(b) No
Question 3.46
![]() 16.
16.
- Discuss scheduling problems for which it is not reasonable to assume that once a processor starts a task, it will always complete that task before it works on any other task. Give examples for which this approach would be reasonable.
- Give an example where the assumption that all processors have identical capabilities in a scheduling situation is not realistic.
Question 3.47
17. Can you give examples of scheduling problems for which it seems reasonable to assume that all the task times are the same?
17.
Answers will vary.
Question 3.48
18. Use the list-processing algorithm to schedule the tasks in the accompanying order-requirement digraph on
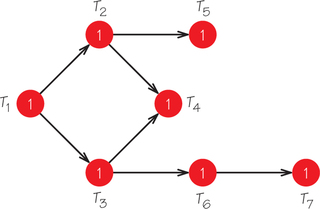
- two processors using the list T1, …, T7.
- two processors using the list T1, T2, T3, T4, T6, T5, T7.
- Is either of the schedules that you obtain optimal?
Question 3.49
19.
 For the accompanying order-requirement digraph, apply the list-processing algorithm, using three processors for lists (a) through (c). How do the completion times obtained compare with the length of the critical path?
For the accompanying order-requirement digraph, apply the list-processing algorithm, using three processors for lists (a) through (c). How do the completion times obtained compare with the length of the critical path?
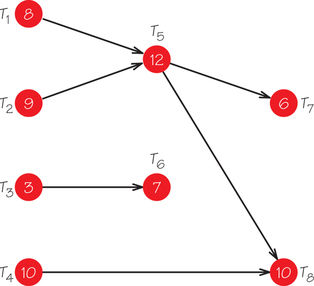
- T1, T2, T3, T4, T5, T6, T7, T8
- T1, T3, T5, T7, T2, T4, T6, T8
- T8, T6, T4, T2, T1, T3, T5, T7
19.
(a) Processor 1: T1,T6, idle 15 to 21, T7, idle 27 to 31; Processor 2: T2,T5,T8; Processor 3: T3,T4, idle from 13 to 31
(b) Processor 1: T1,T6, idle 15 to 21, T7, idle 27 to 31; Processor 2: T3,T4, idle from 13 to 21, T8; Processor 3: T2,T5, idle from 21 to 31
(c) Processor 1: T4, idle 10 to 11, T6, idle 18 to 21, T8; Processor 2: T2,T5,T7, idle 27 to 31; Processor 3: T1,T3, idle 11 to 31
Question 3.50
20.
- Can you find an order-requirement digraph with four tasks for which every priority list used to schedule the tasks on two machines assigns task T4 to machine 1 at time 0?
- Can you choose the order-requirement digraph in part (a) so that machine 2 stays idle for all lists from time 0 to time 3?
Question 3.51
21. Can you find a list that gives rise to the optimal schedule shown in Figure 3.14 (on page 93) for the order-requirement digraph in Figure 3.12 (on page 92)?
21.
Yes
Question 3.52
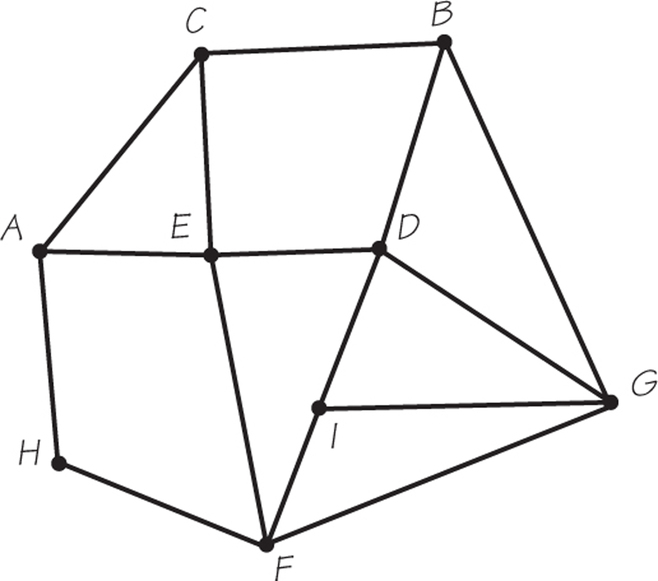
22. Consider the accompanying order-requirement digraph.
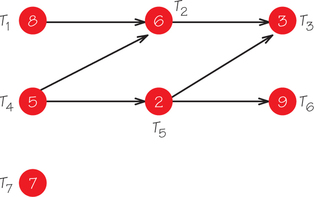
- Find the critical path(s).
- Schedule these tasks on one processor using the critical-path scheduling method.
- Schedule these tasks on one processor using the priority list obtained by listing the tasks in order of decreasing time.
- Does either of these schedules have idle time? How do their completion times compare?
- If two different schedules have the same completion time, what criteria can be used to say one schedule is superior to the other?
- Schedule these tasks on two processors using the order-requirement digraph shown and the priority list from part (b).
- Does the schedule produced in part (f) finish in half the time that the schedule in part (b) did, which might be expected, since the number of processors has doubled?
- Schedule the tasks on (i) one processor and (ii) two processors (using the decreasing-time list), assuming that each task time has been reduced by 1. Do the changes in completion time agree with your expectations?
Question 3.53
23. Given the order-requirement digraph below, answer the following questions.
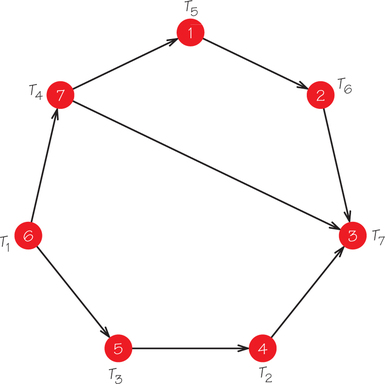
- Find the length of the shortest path from T1 to T2.
- What is the length of the critical path?
- Give a schedule that completes the tasks by the time length of the critical path on two machines, or explain why this is not possible. (If it is possible, provide a list that gives rise to this schedule.)
23.
(a) 15
(b) 19
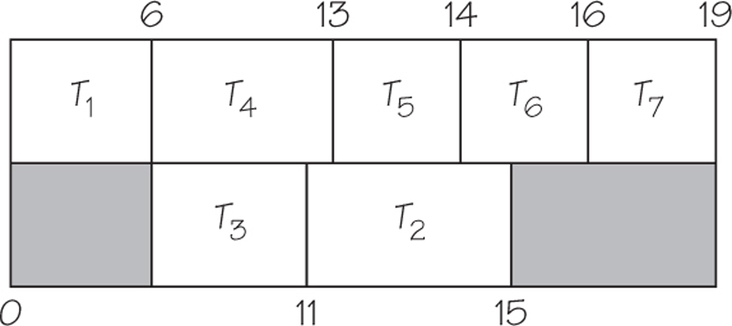
(c) Use the list T1,T4,T3,T2,T5,T6,T7 to obtain the following schedule:
Question 3.54
24.
- The order-requirement diagram accompanying Exercise 23 shows a directed edge from T4 to T7. Explain why this edge can be omitted from the order-requirement digraph because it is “redundant.”
- In Exercise 23, if the direction of the edge from T6 to T7 were reversed, would this still be a “legal” order-requirement digraph? (Explain your answer.)
Question 3.55
25.
- Can all the processors being used to schedule tasks be simultaneously idle at a time before the completion time of a collection of tasks scheduled using the list-processing algorithm?
- Explain why the list-processing algorithm cannot yield the schedule below, regardless of what priority list was used to schedule the tasks on the three processors.
- Construct an order-requirement digraph and a priority list that will yield the following schedule on two processors.
25.
(a) No
(b) If T5 could be started on Machine 3 and Machine 2 was also free at the same time, proper use of the list-processing algorithm should have assigned this task to Machine 2.
(c) Use the digraph with no edges and the list T2, T5, T4, T3, T1.
Question 3.56
26. To prepare a meal quickly involves carrying out the tasks shown (time lengths in minutes) in the accompanying order-requirement digraph:
- If Mike prepares the meal alone, how long will it take?
- If Mike can talk Mary into helping him prepare the meal, how long will it take them if the tasks are scheduled using the list T5, T9, T1, T3, T2, T6, T8, T4, T7 and the list-processing algorithm?
- If Mike can talk Mary and Jack into helping him prepare the meal, how long will it take if the tasks are scheduled using the same list as in part (b)?
- What would be a reasonable set of criteria for choosing a priority list in this situation?
Question 3.57
27.
- Making use of the order-requirement digraph below, determine at time 0 which tasks are ready.
- What is special about tasks T1 and T6?
- What is the critical path, and what is its length?
- Schedule the tasks on three processors with the priority list T1, …, T6.
- Is the schedule found in part (d) optimal?
- Schedule the tasks on three processors using the priority list T6, …, T1.
- Is the schedule found in part (f) optimal?
- Can you find a priority list that yields an optimal schedule?
27.
(a) T1, T2, T3, and T6
(b) No tasks require that T1 and T6 be done before these other tasks can begin.
(c) T6
(d) Processor 1: T1, T6; Processor 2: T2, T4, idle from 18 to 30; Processor 3: T3, T5, idle from 12 to 30
(e) No
(f) Processor 1: T6, idle from 20 to 22; Processor 2: T3, T5, T1; Processor 3: T2, T4, idle from 18 to 22
(g) Yes
(h) Yes
Question 3.58
28.
- In Exercise 27, what priority list would be used if you applied the critical-path scheduling method?
- Use this priority list to schedule the tasks on three processors. Is this schedule optimal?
- How does this schedule compare with the schedules that you found using the lists in Exercise 27?
Question 3.59
29. Consider the following order-requirement digraph. Suppose one plans to schedule these tasks on two identical processors.
- How many different priority lists can be used to schedule the tasks?
- Can all these priority lists lead to different schedules? If not, why not?
- Can an optimal schedule have no idle time? Can you give two different reasons why an optimal schedule must have some idle time?
- Is there any list that produces a schedule where the second processor has no idle time?
29.
(a) 120
(b) No; T1 must be assigned to the first machine at time 0.
(c) No; when 2 divides 31, there is a remainder of 1.
(d) No
Question 3.60
30.
- In Exercise 29, how many different lists are there that do not list T1 first?
- Would it make any sense not to list T1 first in a list?
- Construct a list and schedule the tasks on two processors.
- Can you find another list that leads to a different completion time than the schedule you found for part (c)?
- Find a list that leads to an optimal schedule.
Question 3.61
31. Can you find an order-requirement digraph with four tasks for which every possible list yields exactly the same schedule?
31.
Yes
Question 3.62
32. Can you find an order-requirement digraph involving three tasks such that the schedule corresponding to every list is different?
Question 3.63
33. At a large toy store, scooters arrive unassembled in boxes. To assemble a scooter, the following tasks must be performed:
- Task 1. Remove parts from the box.
- Task 2. Attach wheels to the footboard.
- Task 3. Attach vertical housing.
- Task 4. Attach handlebars to vertical housing.
- Task 5. Put on reflector tape.
- Task 6. Attach bell to handlebars.
- Task 7. Attach decals.
- Task 8. Attach kickstand.
- Task 9. Attach safety instructions to handlebars.
- Give reasonable time estimates for these tasks and construct a reasonable order-requirement digraph. What is the earliest time by which these tasks can be completed?Page 114
- Schedule this job on two processors (humans) using the decreasing-time-list algorithm.
33.
Answers will vary.
Question 3.64
34. If two schedules for the same number of processors have the same completion time, can one schedule have more idle time than the other?
Question 3.65
35. Could the schedule below be obtained by applying the list-scheduling algorithm to some order-requirement digraph?
35.
No
3.3 Independent Tasks
Question 3.66
36. Could the following schedule be obtained by applying the list-scheduling algorithm to some order-requirement digraph?
Question 3.67
37. For the accompanying schedules, can you produce a list so that the list-processing algorithm produces the schedule shown when the tasks are independent? What are the times for each task?
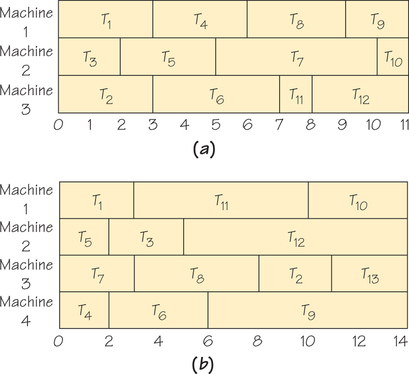
37.
(a) Task times: T1 = 3, T2 = 3, T3 = 2, T4 = 3, T5 = 3, T6 = 4, T7 = 5, T8 = 3, T9 = 2, T10 = 1, T11 = 1, and T12 = 3. This schedule would be produced from the list T1, T3, T2, T5, T4, T6, T7, T8, T11, T12, T9, T10.
(b) Task times: T1 = 3, T2 = 3, T3 = 3, T4 = 2, T5 = 2, T6 = 4, T7 = 3, T8 = =, T9 = 8, T10 = 4, T11 = 7, T12 = 9, and T13 = 3. This schedule would be produced from the list
Question 3.68
![]() 38. Once an optimal schedule has been found for independent tasks (see the diagrams in Exercise 37), usually the scheduling of the tasks can be rearranged and the same optimal time achieved.
38. Once an optimal schedule has been found for independent tasks (see the diagrams in Exercise 37), usually the scheduling of the tasks can be rearranged and the same optimal time achieved.
We can, among other things, reorder the tasks done by a particular processor. Discuss criteria that might be used to implement the rearrangement process.
Question 3.69
39. The task times of eight independent tasks T1 to T8 are 1, 2, 3, 4, 5, 6, 7, 8.
- Schedule the tasks on two processors using the lists (i) T1, T2, …, T8 and (ii) T8, T7, …, T1.
- Is either of the schedules you get in part (a) optimal? If not, find a list that gives an optimal schedule.
39.
(a) (i) Processor 1: T1, T3, T5, T7, idle from 16 to 20; Processor 2: T2, T4, T6, T8
(ii) Processor 1: T8, T5, T4, T1; Processor 2: T7, T6, T3, T2
(b) Yes
Question 3.70
40. Repeat Exercise 39, but schedule the tasks (with the same lists) on three processors. If the schedules you get are not optimal, find a list that gives an optimal schedule.
Question 3.71
![]() 41. Discuss different criteria that might be used to construct a priority list for a scheduling problem.
41. Discuss different criteria that might be used to construct a priority list for a scheduling problem.
41.
Answers will vary.
Question 3.72
![]() 42. Some scheduling projects have due dates for tasks (times by which a given task should be completed) and release dates (times before which a task cannot have work begun on it). Give examples of circumstances where these situations might arise.
42. Some scheduling projects have due dates for tasks (times by which a given task should be completed) and release dates (times before which a task cannot have work begun on it). Give examples of circumstances where these situations might arise.
Question 3.73
43. Using the lists you found in Exercise 37 and the task times you computed for those independent tasks, schedule the tasks for part (a) on four processors and the tasks for part (b) on five processors. Can you see why for any schedule you may produce for part (a) on four processors and part (b) on five processors, there must be some idle time for one or more processors?
43.
In part (a), 33 is not exactly divisible by 4; in part (b), 56 is not exactly divisible by 5.
Question 3.74
44. Use the order-requirement digraph below to answer the following questions.
- Use the list-processing algorithm to schedule these seven tasks on two processors using these lists:
- T1, T3, T7, T2, T4, T5, T6
- T1, T3, T2, T4, T5, T6, T7
- The list obtained by listing the tasks in order of decreasing time
Page 115 - Try to determine whether any of the resulting schedules are optimal.
- Schedule the tasks using the critical-path scheduling method. Try to determine whether this schedule is optimal.
Question 3.75
45. Repeat the questions in Exercise 44 using the order-requirement digraph obtained by erasing all the (directed) edges shown there. How do the schedules you obtain compare with the ones you originally got?
45.
(a) (i) Machine 1: 12, 9, 15, idle from 36 to 50; Machine 2: 7, 10, 13, 20
(ii) Machine 1: 12, 13, 20; Machine 2: 7, 9, 15, 10, idle from 41 to 45
(iii) Machine 1: 20, 12, 9, idle from 41 to 45; Machine 2: 15, 13, 10, 7
(b) None of the schedules found is optimal
(c) The critical path list is T6, T5, T4, T1, T7, T2, T3. This list does not lead to an optimal schedule, but there is a schedule where the completion time is 43, achievable by scheduling the tasks of length 20, 13, and 10 on Machine 1 and tasks of length 24 and 19 on Machine 2.
Question 3.76
46.
- Find the completion time for independent tasks of length 8, 11, 17, 14, 16, 9, 2, 1, 18, 5, 3, 7, 6, 2, 1 on two processors, using the list-processing algorithm.
- Find the completion time for the tasks in part (a) on two processors, using the decreasing-time-list algorithm.
- Does either algorithm give rise to an optimal schedule?
- Repeat for tasks of lengths 19, 19, 20, 20, 1, 1, 2, 2, 3, 3, 5, 5, 11, 11, 17, 18, 18, 17, 2, 16, 16, 2.
Question 3.77
47. Repeat parts (a)–(c) of Exercise 46 for independent tasks of lengths 19, 19, 20, 20, 1, 1, 2, 2, 3, 3, 5, 5, 11, 11, 17, 17, 18, 18, 17, 2, 16, 16, 2.
47.
(a) Machine 1: 129; Machine 2: 129
(b) Machine 1: 123; Machine 2: 123
(c) Yes
Question 3.78
48. Suppose that independent tasks require a total of 36 minutes, but only one of the tasks takes as long as 12 minutes. If these tasks are scheduled on two machines, show by an example that the earliest completion time may be as long as 22 minutes.
Question 3.79
49. A photocopy shop must schedule independent batches of documents to be copied. The times for the different sets of documents are (in minutes) 12, 23, 32, 13, 24, 45, 23, 23, 14, 21, 34, 53, 18, 63, 47, 25, 74, 23, 43, 43, 16, 16, 76.
- Construct a schedule using the list-processing algorithm on three machines.
- Construct a schedule using the list-processing algorithm on four machines.
- Repeat parts (a) and (b), but use the decreasing-time-list algorithm.
- Suppose union regulations require that an 8-minute rest period be allowed for any photocopy task over 45 minutes. Use the decreasing-time-list algorithm, with the preceding times modified to take into account the union requirement, to schedule the tasks on three human-operated machines.
49.
(a) Processor 1: 12, 13, 45, 34, 63, 43, 16, idle 226 to 298; Processor 2: 23, 24, 23, 53, 25, 74, 76; Processor 3: 32, 23, 14, 21, 18, 47, 23, 43, 16, idle 237 to 298
(b) Processor 1: 12, 24, 14, 34, 25, 23, 16, 16, 76; Processor 2: 23, 23, 21, 63, 43, idle 173 to 240; Processor 3: 32, 23, 53, 74, idle 182 to 240; Processor 4: 13, 45, 18, 47, 43, idle 166 to 240
(c) Three machines: Processor 1: 76, 45, 43, 24, 23, 18, 16, 13; Processor 2: 74, 47, 34, 32, 23, 21, 14, 12, idle 257 to 258; Processor 3: 63, 53, 43, 25, 23, 23, 16, idle 246 to 248 Four machines: Processor 1: 76, 43, 24, 23, 16, idle 182 to 194; Processor 2: 74, 43, 25, 23, 16, 13; Processor 3: 63, 45, 32, 23, 18, 12, idle 193 to 194; Processor 4: 53, 47, 34, 23, 21, 14, idle 192 to 194
(d) Processor 1: 84, 45, 43, 25, 23, 23, 16, 12; Processor 2: 82, 55, 34, 32, 23, 18, 14, 13; Processor 3: 71, 61, 43, 24, 23, 21, 16, idle 259 to 271
Question 3.80
50. Find a list that produces the following optimal schedule when the list-processing algorithm is applied to this list. (Assume that the tasks are independent.)
What completion time and schedule are obtained when the decreasing-time-list algorithm is applied to this list?
Question 3.81
51. Can you think of situations other than those mentioned in the text where scheduling independent tasks on processors occurs?
51.
Answers will vary.
Question 3.82
52. Can you think of real-world scheduling situations in which all the tasks have the same time and are independent? Find an algorithm for solving this problem optimally. (If there are n independent tasks of time length k, when will all the tasks be finished?)
Question 3.83
53. Show that when tasks to be scheduled are independent, the critical-path method and the decreasing-time-list method are identical.
53.
Each task heads a path of length equal to the time to do that task.
3.4 Bin Packing
Question 3.84
54. Two wooden wall systems are to be made of pieces of wood with lengths shown in the accompanying diagram. If wood is sold in 10-foot planks and can be cut with no waste, what number of boards would be purchased if one uses the FFD, NFD, and WFD heuristics, respectively?
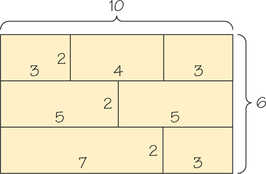
In solving this problem, does it make a difference if the 10-foot horizontal shelves and 6-foot vertical boards employ single-length pieces, compared with using pieces of boards that add up to 10- and 6-foot lengths?
Question 3.85
55. It takes 4 seconds to photocopy one page. Manuscripts of 10, 8, 15, 24, 22, 24, 20, 14, 19, 12, 16, 30, 15, and 16 pages are to be photocopied. How many photocopy machines would be required, using the FFD algorithm, to guarantee that all manuscripts are photocopied in 2 minutes or less? Would the solution differ if WFD were used?
55.
9; number of bins would not change, but the placement of the items in the bins would differ.
Question 3.86
56. A radio station’s policy allows advertising breaks of no longer than 2 minutes, 15 seconds. Using FF and FFD algorithms, determine the minimum number of breaks into which the following ads will fit (lengths given in seconds): 80, 90, 130, 50, 60, 20, 90, 30, 30, 40. Can you find the optimal solution? Do the same for these ad lengths: 60, 50, 40, 40, 60, 90, 90, 50, 20, 30, 30, 50.
Question 3.87
57. Fiberglass insulation comes in 36-inch pre-cut sections. A plumber must install insulation in a basement on piping that is interrupted often by joints. The distances between the joints on the stretches of pipe that must be insulated are 12, 15, 16, 12, 9, 11, 15, 17, 12, 14, 17, 18, 19, 21, 31, 7, 21, 9, 23, 24, 15, 16, 12, 9, 8, 27, 22, 18 inches. How many pre-cut sections would he have to use to provide the insulation if he bases his decision on
- next fit?
- next-fit decreasing?
- worst fit?
- worst-fit decreasing?
57.
(a) 17
(b) 16
(c) 16
(d) 13
Question 3.88
58. The files that a company has for its employees dealing with utilities occupy 100, 120, 60, 90, 110, 45, 30, 70, 60, 50, 40, 25, 65, 25, 55, 35, 45, 60, 75, 30, 120, 100, 60, 90, 85 sectors. If, after operating systems are installed, a disk can store up to 480 sectors, determine the number of disks needed to store the utilities if each of these heuristics is used to pack the disk with files.
- Next fit
- Next-fit decreasing
- First fit
- First-fit decreasing
Question 3.89
59. Advertisements for the TV show Q are permitted to last up to a total of 8 minutes, and each group of ads can last up to 2 minutes. If the ads slated for Q last 63, 32, 11, 19, 24, 87, 64, 36, 27, 42, 63 seconds, determine whether FF and FFD yield acceptable configurations for the ads.
59.
Yes, both are acceptable.
Question 3.90
60. Consider the heuristic for packing bins known as best fit described as follows: Keep track of how much room remains in each unfilled bin and put the next item to be packed into that bin that would leave the least room left over after the item is put into the bin. (For example, suppose that bin 4 had 6 units left, bin 7 had 5 units left, and bin 9 had 8 units left. If the next item in the list had size 5, then first fit would place this item in bin 4, worst fit would place the item in bin 9, while best fit would place the item in bin 7.) If there is a tie, place the item in the bin with the lowest number. Apply this heuristic to the list 8, 7, 1, 9, 2, 5, 7, 3, 6, 4, where the bins have capacity 10.
Question 3.91
![]() 61. We have described two algorithms for bin packing called worst fit and best fit (see page 97 and Exercise 60). The words best and worst have connotations in English. However, the performance of algorithms depends on their merits as algorithms, not on the names we give them.
61. We have described two algorithms for bin packing called worst fit and best fit (see page 97 and Exercise 60). The words best and worst have connotations in English. However, the performance of algorithms depends on their merits as algorithms, not on the names we give them.
- On the basis of experiments you perform with the best-fit and worst-fit algorithms, which one do you think is the “better” of the two?
- Can you construct an example where worst fit uses fewer bins than best fit?
61.
(a) Answers will vary.
(b) It is possible.
Question 3.92
62. The best-fit heuristic (see Exercise 60) also has a “decreasing” version, where the list is first sorted in decreasing order. Using bins of capacity 10, apply the best-fit heuristic and its decreasing version to the following list: 6, 9, 5, 8, 3, 2, 1, 9, 2, 7, 2, 5, 4, 3, 7, 6, 2, 8, 3, 7, 1, 6, 4, 2, 5, 3, 7, 2, 5, 2, 3, 6, 2, 7, 1, 3, 5, 4, 2, 6.
Question 3.93
![]() 63. One pianist’s recording of the complete Mozart piano sonatas takes the following times (given in minutes and seconds): 13:46, 6:15, 3:29, 5:37, 7:52, 2:55, 5:00, 4:28, 4:21, 7:39, 7:55, 6:42, 4:23, 3:52, 4:21, 4:20, 5:46, 6:29, 5:34, 6:23, 6:39, 7:19, 5:54, 6:54, 2:58, 5:22, 1:42, 5:00, 1:29, 5:47, 7:30, 8:19, 4:44, 4:57, 4:09, 14:31, 3:55, 4:04, 4:01, 6:06, 6:50, 5:27, 4:28, 5:40, 2:52, 5:16, 5:34, 3:10, 7:22, 4:40, 3:08, 6:32, 4:47, 6:59, 5:38, 7:57, 3:38. If the maximum time that can be recorded on a compact disc is 70:30, can all the music be performed on four compact discs? Can all the music be performed on five compact discs?
63. One pianist’s recording of the complete Mozart piano sonatas takes the following times (given in minutes and seconds): 13:46, 6:15, 3:29, 5:37, 7:52, 2:55, 5:00, 4:28, 4:21, 7:39, 7:55, 6:42, 4:23, 3:52, 4:21, 4:20, 5:46, 6:29, 5:34, 6:23, 6:39, 7:19, 5:54, 6:54, 2:58, 5:22, 1:42, 5:00, 1:29, 5:47, 7:30, 8:19, 4:44, 4:57, 4:09, 14:31, 3:55, 4:04, 4:01, 6:06, 6:50, 5:27, 4:28, 5:40, 2:52, 5:16, 5:34, 3:10, 7:22, 4:40, 3:08, 6:32, 4:47, 6:59, 5:38, 7:57, 3:38. If the maximum time that can be recorded on a compact disc is 70:30, can all the music be performed on four compact discs? Can all the music be performed on five compact discs?
63.
No; yes
Question 3.94
![]() 64. In the wall-system example in the text, first fit and worst fit required equal numbers of bins (see Figure 3.20 on page 97). Can you find an example where first fit and worst fit yield different numbers of bins? Can you find an example where first fit, worst fit, and next fit yield answers with different numbers of bins?
64. In the wall-system example in the text, first fit and worst fit required equal numbers of bins (see Figure 3.20 on page 97). Can you find an example where first fit and worst fit yield different numbers of bins? Can you find an example where first fit, worst fit, and next fit yield answers with different numbers of bins?
Question 3.95
![]() 65. A common suggestion for heuristics for the bin-packing problem with bins of capacity W involves finding weights that sum to exactly W. Discuss the pros and cons of a heuristic of this type.
65. A common suggestion for heuristics for the bin-packing problem with bins of capacity W involves finding weights that sum to exactly W. Discuss the pros and cons of a heuristic of this type.
65.
Answers will vary.
Question 3.96
![]() 66. A recording company wishes to record all the Beethoven string quartets (16 quartets, each consisting of several consecutive parts called movements) on reissued LPs. It wishes to complete the project on as few records as possible. Recording can be done on two sides as long as the movements are consecutive. Is this an example of a bin-packing problem? (Defend your answer.) If the project were to record the quartets on (standard) tape cassettes or compact discs, would your answer be different?
66. A recording company wishes to record all the Beethoven string quartets (16 quartets, each consisting of several consecutive parts called movements) on reissued LPs. It wishes to complete the project on as few records as possible. Recording can be done on two sides as long as the movements are consecutive. Is this an example of a bin-packing problem? (Defend your answer.) If the project were to record the quartets on (standard) tape cassettes or compact discs, would your answer be different?
Question 3.97
67. Give examples where it would be realistic to keep bins open as more items “arrive” to be packed, rather than to close a bin permanently based on some criterion.
67.
Answers will vary.
Question 3.98
68. Give examples where it would be unrealistic to keep bins open as more items “arrive” to be packed, rather than to close a bin permanently based on some criterion.
Question 3.99
69. A data entry group must handle 30 (independent) tasks that will take the following amounts of time (in minutes) to type: 25, 18, 13, 19, 30, 32, 12, 36, 25, 17, 18, 26, 12, 15, 31, 18, 15, 18, 16, 19, 30, 12, 16, 15, 24, 16, 27, 18, 9, 14. Use these times as a priority list.
- Use the list-processing algorithm to find the completion time for scheduling tasks with four secretaries. Also, solve with five secretaries.
- Repeat the scheduling using the decreasing-time-list algorithm.
- Can you show that any of the schedules you get are optimal?
Say the typing needs to be finished in 1 hour.
- Use the FFD heuristic to find how many typists are needed.
- Repeat for the NFD and WFD heuristics.
- Can you show that any of the solutions you get are optimal?
69.
(a) 152 min; 124 min
(b) 155 min; 120 min
(c) Yes; five-processor decreasing-time schedule
(d) 11
(e) NFD: 13; WFD: 11
(f) An optimal packing with 10 bins exists.
Question 3.100
70. Find the minimum number of bins necessary to pack items of size 8, 5, 3, 4, 3, 7, 8, 8, 6, 5, 3, 2, 1, 2, 1, 2, 1, 3, 5, 2, 4, 2, 6, 5, 3, 4, 2, 6, 7, 7, 8, 6, 5, 4, 6, 1, 4, 7, 5, 1, 2, 4 in bins of capacity (a) through (d) using the FF and FFD algorithms. Can you determine whether any of the packings you get are optimal?
- 9
- 10
- 11
- 12
Question 3.101
![]() 71. Two-dimensional bin packing refers to the problem of packing rectangles of various sizes into a minimum number of m×n rectangles, with the sides of the packed rectangles parallel to those of the containing rectangle.
71. Two-dimensional bin packing refers to the problem of packing rectangles of various sizes into a minimum number of m×n rectangles, with the sides of the packed rectangles parallel to those of the containing rectangle.
- Suggest some possible real-world applications of this problem.
- Devise a heuristic algorithm for this problem.
- Give an argument to show that the problem is at least as hard to solve as the usual bin-packing problem.
- If you have 1×m rectangles with total area W to be packed into a single rectangle of area p×q=W, can the packing always be accomplished?
71.
(a) Answers will vary.
(b) Answers will vary.
(c) Packing rectangles of width 1 in an m×1 rectangle is a special case of the two-dimensional problem.
(d) Answers will vary.
Question 3.102
![]() 72. In what situations would packing bins of different capacities be the appropriate model for real-world situations? Suggest some possible algorithms for this type of problem.
72. In what situations would packing bins of different capacities be the appropriate model for real-world situations? Suggest some possible algorithms for this type of problem.
Question 3.103
![]() 73. Find an example of weights that, when packed into bins using first fit, use fewer bins than the number of bins used when the first-fit algorithm is applied with the first weight on the list removed.
73. Find an example of weights that, when packed into bins using first fit, use fewer bins than the number of bins used when the first-fit algorithm is applied with the first weight on the list removed.
73.
Answers will vary.
Question 3.104
![]() 74. Formulate “paradoxical” situations for bin packing that are analogous to those we found for scheduling processors.
74. Formulate “paradoxical” situations for bin packing that are analogous to those we found for scheduling processors.
3.5 Resolving Conflict via Coloring
Question 3.105
75. Draw a connected graph with 12 vertices and 11 edges whose vertices can be colored with two colors.
75.

Question 3.106
76. Add a single edge to the graph you drew for Exercise 75 so that the vertices of the resulting graph cannot be colored with two colors but require three colors.
Question 3.107
77. For each of the graphs below, answer the following questions.
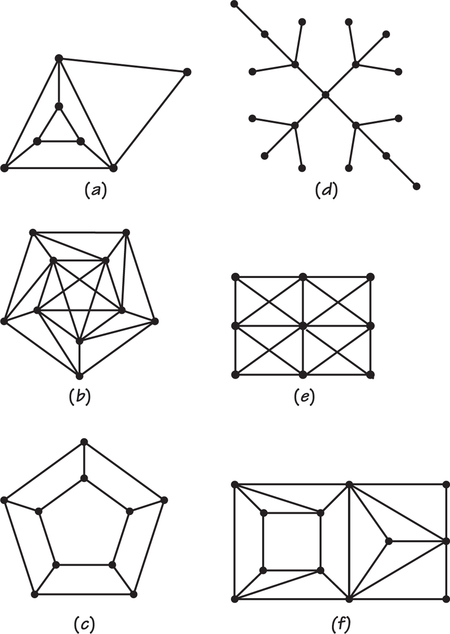
- Color the vertices (if possible) with three different colors.
- Color the vertices (if possible) with four different colors.
- Find the chromatic number of the graph.
77.
(a) Graph in: (a) Yes (b) No (c) Yes (d) Yes (e) No (f) No
(b) Graph in: (a) Yes (b) No (c) Yes (d) Yes (e) Yes (f) Yes
(c) Graph in: (a) 3 (b) 5 (c) 3 (d) 2 (e) 4 (f) 4
Question 3.108
78. For each of the accompanying graphs, answer the following questions.
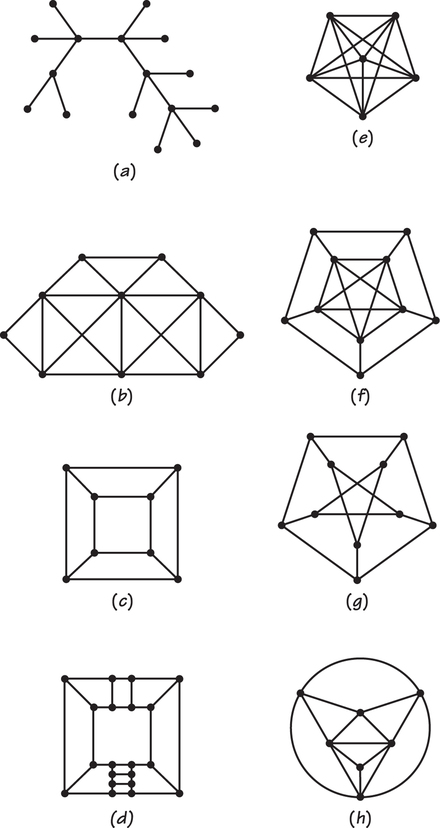
- Color the vertices (if possible) with two different colors.
- Color the vertices (if possible) with three different colors.
- Find the chromatic number of the graph.
Question 3.109
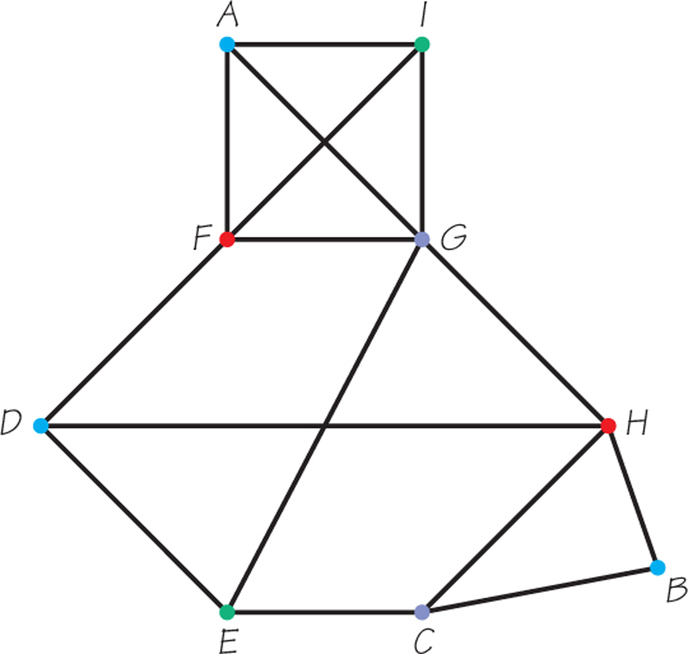
79. The owner of a new pet store wishes to display tropical fish in display tanks. The accompanying table shows the incompatibilities between the species, in the sense that an X indicates that it is unwise to allow those species in the row and column that meet at the X to be in the same tank.
| A | B | C | D | E | F | G | H | I | |
| A | X | X | X | ||||||
| B | X | X | |||||||
| C | X | X | X | ||||||
| D | X | X | X | ||||||
| E | X | X | X | ||||||
| F | X | X | X | X | |||||
| G | X | X | X | X | X | ||||
| H | X | X | X | X | |||||
| I | X | X | X |
- Draw an appropriate graph to represent the information in the table.
- What is the minimum number of tanks needed to display all the fish she wishes to sell?
- Display the species so that the number of species in each tank is as nearly equal as possible.
79.
(a) Drawings can vary. Possible renderings include the following:
(b) 4
(c) The coloring in part (a) indicates one possible arrangement.
Question 3.110
80. The managers of a zoo are planning to open a small satellite branch. The animals are to be in enclosures in which compatible animals are displayed together. The accompanying table indicates those pairs of animals that are compatible. (Thus, an X in a particular row and column means that the animals that label this row and column can share an enclosure.)
| A | B | C | D | E | F | G | H | I | J | |
| A | X | X | X | X | X | X | ||||
| B | X | X | X | X | X | X | X | |||
| C | X | X | X | X | ||||||
| D | X | X | X | X | X | X | X | |||
| E | X | X | X | X | X | X | X | |||
| F | X | X | X | X | X | X | X | X | ||
| G | X | X | X | X | X | X | X | |||
| H | X | X | X | X | ||||||
| I | X | X | X | X | X | |||||
| J | X | X | X |
- Draw an appropriate graph to represent the information in the table.
- What is the minimum number of enclosures needed to avoid housing incompatible animals in the same enclosure?
- Is it possible to enclose the animals in such a way that each enclosure contains the same number of animals?
- Why might that be desirable? Why might this approach to grouping the animals not be ideal?
Question 3.111
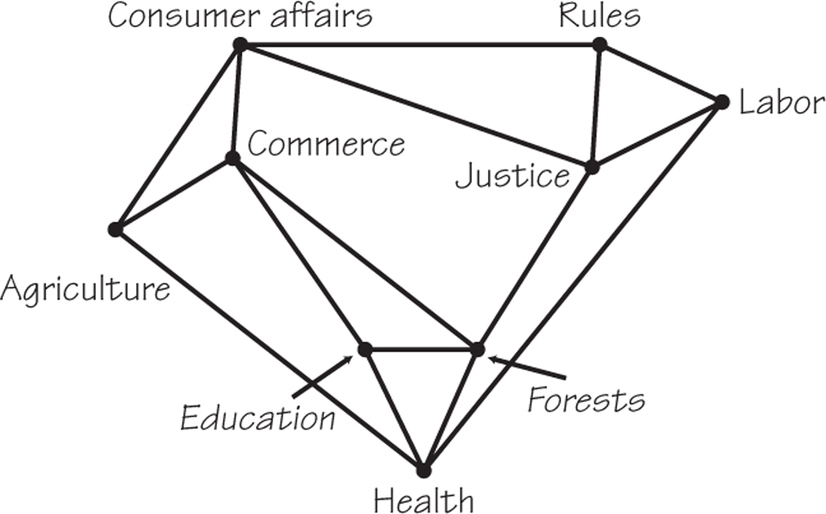
81. The nine standing committees of a state legislature are designing a schedule for when the committees can meet. The matrix shown in the following table has an X in a position where the committees corresponding to the row and column have a common member and, hence, should not be scheduled to meet at the same hour. The committees involved are Agriculture (A), Commerce (C), Consumer Affairs (CA), Education (E), Forests (F), Health (H), Justice (J), Labor (L), and Rules (R).
| A | C | CA | E | F | H | J | L | R | |
| A | X | X | X | ||||||
| C | X | X | X | X | |||||
| CA | X | X | X | X | |||||
| E | X | X | X | ||||||
| F | X | X | X | X | |||||
| H | X | X | X | X | |||||
| J | X | X | X | X | |||||
| L | X | X | X | ||||||
| R | X | X | X |
- Draw a graph that will be of value in determining the minimum number of time slots the committees can meet in without any legislator having to be in two places at one time.
- What is the minimum number of time slots in which the committees can be scheduled without a conflict?
- How many different rooms are needed at any time that a committee is scheduled to meet? (Why might this issue matter?)
81.
(a) Drawings can vary. Possible renderings include the following:
(b) 3
(c) 3; additional answers will vary.
Question 3.112
82. Determine the minimum number of colors, and how often each color is used, in a vertex coloring of the graphs below.
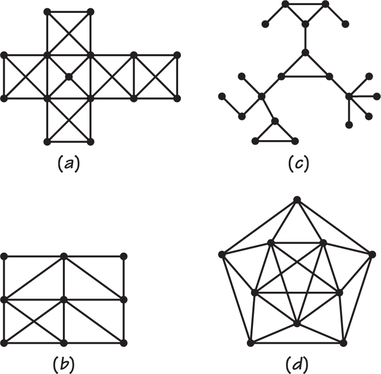
Question 3.113
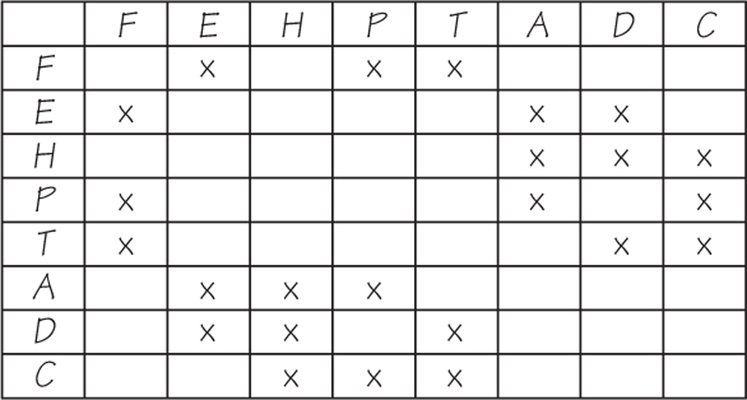
83. The faculty-student governing council at All State College has nine standing committees (such as Curriculum, Academic Standards, Campus Life) that are designated A,B,C,D,…,I for convenience. The following table shows which committees have no member in common:
| A | B | C | D | E | F | G | H | I | |
| A | X | X | X | X | X | ||||
| B | X | X | X | X | X | ||||
| C | X | X | X | X | X | ||||
| D | X | X | X | X | |||||
| E | X | X | X | X | |||||
| F | X | X | X | X | |||||
| G | X | X | X | X | |||||
| H | X | X | X | X | X | X | |||
| I | X | X | X | X | X |
- Draw an appropriate graph to represent the information in the table.
- What is the minimum number of time slots in which all the committee meetings can be scheduled?
- How many rooms are needed during each time slot to accommodate the committees that are scheduled to meet in that time slot?
83.
(a) Drawings can vary. Possible renderings include the following:
(b) 3
(c) 3
Question 3.114
84. When two towns are within 145 miles of each other, the frequency used by a certain type of emergency response system for the towns requires that they be on different frequencies to avoid possible interference with each other. The following table shows the mileage distances between six towns:
| E | F | G | I | S | T | |
| Evansville (E) | 290 | 277 | 168 | 303 | 133 | |
| Ft. Wayne (F) | 290 | 132 | 83 | 79 | 201 | |
| Gary (G) | 277 | 132 | 153 | 58 | 164 | |
| Indianapolis (I) | 168 | 83 | 153 | 140 | 71 | |
| South Bend (S) | 303 | 79 | 50 | 140 | 196 | |
| Terre Haute (T) | 113 | 201 | 164 | 71 | 196 |
- What would be the minimum number of frequencies that are needed for each town to have its emergency broadcasts not conflict with those of any other town using this system?
- How many different towns would be assigned to each frequency used?
Question 3.115
85. The legislature of a city has committees devoted to the following governmental areas:
A=agriculture; P=planning; D=districting; F=finance; E=education; T=transportation; H=housing, C=courts. To schedule meetings for these committees in as few time slots as possible, consider the graph model below.
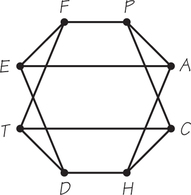
| F | E | H | P | T | A | D | C | |
| F | ||||||||
| E | ||||||||
| H | ||||||||
| P | ||||||||
| T | ||||||||
| A | ||||||||
| D | ||||||||
| C |
- Complete the entries in the table below that would display the “conflict” information represented by the graph, where an X indicates two committees that cannot meet at the same time because they have at least one common member.
- What is the minimum number of time slots in which it is possible to schedule these committees?
- If there are only three rooms with the audio and video setups needed for the committees to meet, what is the minimum number of time slots during which the committees can meet?
85.
(a) Drawings can
(b) 2
(c) 3 (Two rooms will be used for three committee meetings and one room for two committee meetings.)
Question 3.116
86. A small college has a mini-session in January (between its regular semesters) in which nine classes are offered: A=Art; B=Biology, C=Chemistry; D=Diversity; E=English, F=French, G=German, H=Health, I=Italian. The accompanying table indicates those courses that have students in common.
| A | B | C | D | E | F | G | H | I | |
| A | X | X | X | ||||||
| B | X | X | X | ||||||
| C | X | X | X | X | |||||
| D | X | X | X | ||||||
| E | X | X | X | ||||||
| F | X | X | X | X | |||||
| G | X | X | X | X | |||||
| H | X | X | X | X | |||||
| I | X | X | X | X |
- Draw a graph model for the information in this table.
- What is the minimum number of time slots in which final examinations can be scheduled for these nine courses?
- Can this minimum be achieved if only three rooms are large enough to hold the finals?
Question 3.117
87. Show that the vertices of any tree can be colored with two colors.
87.
Answers will vary.
Question 3.118
88. Can you find a family of graphs Hn(n≥1) that require n colors to color their vertices?
Question 3.119
89. The edge-coloring number of a graph G is the minimum number of colors needed to color the edges of G so that edges sharing a common vertex get different colors. Determine the edge-coloring number for each of the graphs in Exercise 77. Can you make a conjecture about the value of the minimum number of colors needed to color the edges of any graph?
89.
Graph in: (a) 8 (b) 5 (c) 6 (d) 4 (e) 3 (f) 4; the minimum is either the largest valence of any vertex or 1 more than the largest valence.
Question 3.120
90. Can you think of any applications that require determining the minimum number of colors needed to color the edges of a graph?
Question 3.121
91. When a graph has been drawn on a piece of paper so that edges meet only at vertices, the graph divides the paper up into regions called faces. The faces include one called the “infinite” face, which surrounds the whole graph. The face-coloring number of a graph G (which can be drawn in this special way) is the minimum number of colors needed to color the faces of G so that two faces sharing an edge receive different colors. (Note that if two faces meet only at a vertex, they can be colored the same color.)
- Determine the minimum number of colors needed to color the faces of the accompanying graphs. In each case, remember to color the infinite face, which is labeled I (for “infinite”).
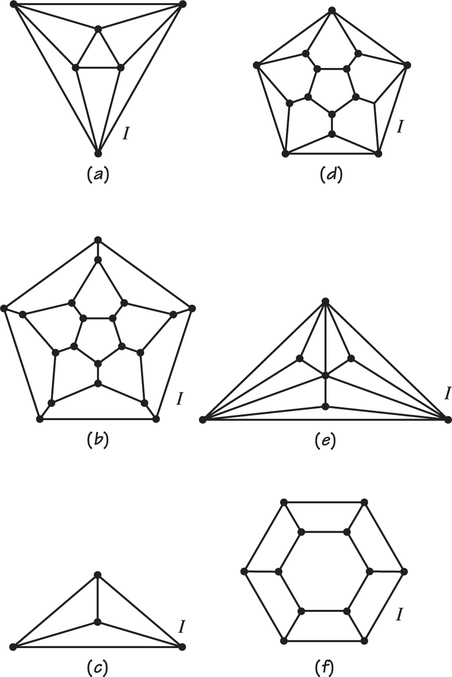
- Can you think of an application of the problem of coloring the faces of a graph with a minimum number of colors?
91.
(a) Graph (a) 2 (b) 4 (c) 4 (d) 4 (e) 3 (f) 3
(b) Answers will vary.
Question 3.122
92. For each of the graphs in Exercise 78 where the graph shown has edges that meet only at vertices, verify that the Four Color Theorem holds by showing that the regions (faces) of the graph can be colored with four or fewer colors so that regions sharing an edge get different colors. (Remember to assign a color to the unbounded, so-called infinite region.)
Question 3.123
93. A company sells herbs, each of which requires a certain level of proper watering. The accompanying graph is constructed by having one vertex for each type of herb. The vertices representing two herbs are joined by an edge if they must have different levels of watering. What is the minimum number of terrariums that the herbs can be displayed in so that herbs in the same terrarium can be watered at the same level?
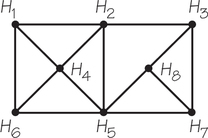
93.
3
Question 3.124
94. The company in Exercise 93 is disappointed by the minimum number of terrariums needed to display the herbs with the proper watering requirements. One company employee suggests that if the information about watering requirements is altered for a single pair of herbs (e.g., a single edge is erased from the diagram), then the number of terrariums needed will be reduced by 1. Is this true?
Question 3.125
95. Each vertex in the graph below represents a child who attends a daycare center. An edge between two children indicates these children tend to cause problems when they are in the same play group. What is the minimum number of play groups that will ensure that no conflicts arise? Can conflict-free play groups with the same number of children in each group be formed?
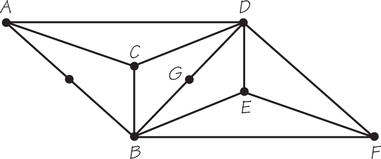
95.
Three play groups will ensure no conflict. Four equalsize conflict-free groups can be formed. These groups would have size 2.
Chapter Review
Question 3.126
96. Determine the minimum number of time slots to schedule the seven committees represented by vertices in the accompanying graph, if edges show which committees cannot meet at the same time.
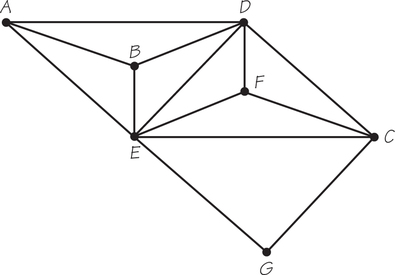
Question 3.127
97. The regions of the accompanying map will appear in an atlas. If the surrounding region (infinite face) is to be colored blue, can the additional regions be colored so that all the regions can be colored with three or fewer colors? Regions sharing only a vertex can be colored with the same color.
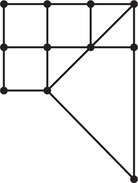
97.
Yes
Question 3.128
98. Given the job J (times shown in months) to publish a new edition of a book consisting of the tasks given in the order-requirement digraph D below, answer the following questions.
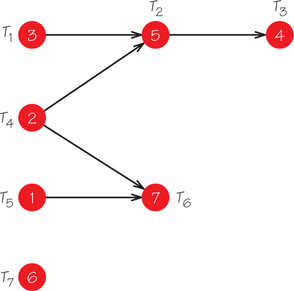
- Determine the length of the critical path(s) in D and list the tasks on the critical path.
- Explain why even with five processors, this job can’t be completed by time 8, which is the total task time divided by 5.
- Schedule the job J using the list algorithm on two processors and the critical-path scheduling method.
- Is the schedule for job J produced in part (c) optimal?
- Can you find an optimal schedule for J scheduled on two processors?
Question 3.129
99.
- Given items with weights 3, 9, 6, 5, 3, 1, 7, 4, 5, 6, determine the number of bins (advertising break slots) in which to pack these items if the bin size is 10 using first fit, next fit, and first-fit decreasing.
- If we interpret these weights as times for independent tasks to be scheduled on machines, what would be the earliest completion time for these tasks scheduled on 3 machines, using the given list?
- If in part (b) we use the decreasing-time list, what is the earliest completion time?
- Is your answer in part (c) optimal?
99.
(a) Contents of bins listed as items from the bottom to the top: First fit: Bin 1: 3, 6, 1; Bin 2: 9; Bin 3: 5, 3; Bin 4: 7; Bin 5: 4, 5; Bin 6: 6. Next fit: Bin 1: 3; Bin 2: 9; Bin 3: 6; Bin 4: 5, 3, 1; Bin 5: 7; Bin 6: 4, 5; Bin 7: 6. First-fit decreasing: Bin 1: 9, 1; Bin 2: 3, 7; Bin 3: 6, 4; Bin 4: 6, 3; Bin 5: 5, 5.
(b) 19
(c) 17
(d) Yes