3.4 3.3 Independent Tasks
Mathematicians suspect that no computationally efficient algorithm for solving general scheduling problems optimally will ever be found. Owing to our limited success in designing algorithms for finding optimal schedules for general order-requirement digraphs, we will consider a special class of scheduling problems for which the order-requirement digraph has no edges. In this case, we say that the tasks are independent of one another, because they can be performed in any order. (No edges in the order-requirement digraph indicates that no tasks need to precede others; that is, the tasks can be done in any order.) In this section, we consider the problem of scheduling independent tasks.
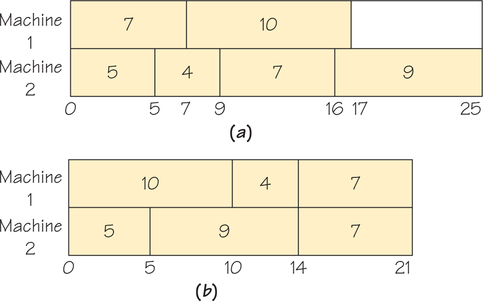
Geometrically, we can think of the independent tasks as rectangles of height 1 whose lengths are equal to the time length of the task. Finding an optimal schedule amounts to packing the task rectangles, with no “idle time” gaps between adjacent rectangles, into a longer rectangle whose height equals the number of machines. For example, Figure 3.15 shows two different ways to schedule tasks of length 10, 4, 5, 9, 7, 7 on two machines. (For convenience, the rectangles in the case of independent tasks are labeled with their task times rather than their task numbers.) Scheduling basically means efficiently packing the task rectangles into the scheduling rectangle. There cannot be processor idle time between independent tasks because no task has to wait for any other task to be completed first. Finding the optimal answer among all possible ways to pack these rectangles is like looking for a needle in a haystack. The list-processing algorithm produces a packing, but it may not be a good one.
There are two approaches we can consider. To study average-case analysis, we might ask: Is the average (mean) of the completion times arrived at by using the list-processing algorithm with all the possible different lists close to the optimal possible completion time? To study worst-case analysis, we might ask: How far from optimal is a schedule obtained using the list-processing algorithm with one particular priority list? What is being contrasted with these two points of view is that an algorithm may work well most of the time (give an answer close to optimal) even though there may be a few cases in which it performs very badly. Average-case analysis is amenable to mathematical solution but requires methods of great sophistication.
Decreasing-Time Lists
Is there some way of choosing a priority list for independent tasks that consistently yields relatively good schedules? The surprising answer is yes! The idea is that when long tasks appear toward the end of the list, they often seem to “stick out” on the right end, as in Figure 3.15a. This suggests that before one tries to schedule a collection of tasks, the tasks should be placed in a list where the longest tasks are listed first.
Decreasing-Time-List Algorithm PROCEDURE
The list-processing algorithm applied to a list of task times arranged in order of nonincreasing size is called the decreasing-time-list algorithm.
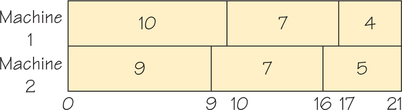
If we apply the decreasing-time-list algorithm to the set of tasks listed previously (10, 4, 5, 9, 7, 7), we obtain the times 10, 9, 7, 7, 5, 4 and the schedule (packing) shown in Figure 3.16. This packing is again optimal, but it is different from the optimal scheduling in Figure 3.15b. It is worth noting that the decreasing-time list and the list obtained by the critical-path method discussed earlier will coincide in the case of independent tasks. The decreasing-time list can also be constructed for the case in which the tasks are not independent. For general order-requirement digraphs, the decreasing-time list does not produce particularly good schedules.
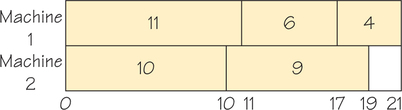
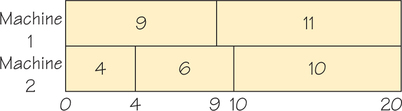
It is important to remember that the decreasing-time-list algorithm does not guarantee optimal solutions. This can be seen by scheduling the tasks with times 11, 10, 9, 6, 4 (Figure 3.17). The schedule has a completion time of 21. However, the rearranged list 9, 4, 6, 11, 10 yields the schedule in Figure 3.18, which finishes at time 20. This solution is obviously optimal because the machines finish at the same time and there is no idle time. Note that when tasks are independent, if there are m machines available, the completion time cannot be less than the sum of the task times divided by m.
Self Check 2
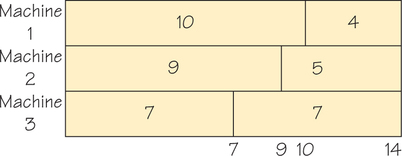
Apply the list-processing algorithm to the independent tasks with times shown in Figure 3.15, using the decreasing-time list with three processors. Is the resulting schedule optimal?
Using the list 10, 9, 7, 7, 5, 4, we get the result in the accompanying figure.
EXAMPLE 4 Photocopy Shop and Data Entry Problems
Photocopy Shop and Data Entry Problems
Imagine a photocopy shop with three photocopiers. Photocopying tasks that must be completed overnight are accepted until 5 P.M. The tasks are to be done in any manner that minimizes the finish time for all the work. Because this problem involves scheduling machines for independent tasks, the decreasing-time-list algorithm would be a good heuristic to apply.
For another example, consider a data entry pool at a large corporation or college, where individual entry tasks can be assigned to any data entry specialist. In this setting, however, the assumption that the data entry workers are identical in skill is less likely to be true. Hence, the tasks might have different times with different processors. This phenomenon, which occurs in real-world scheduling problems, violates one of the assumptions of our mathematical model.
