4 Linear Programming and the Transportation Problem

Skills Check

Question 4.1

1. Where do the lines $3 x + 5 y = 26$ and $2 x + 3 y = 16$ intersect?

At the point (2, 4)
At the point (6, 2)
At the point (4, 2)

Question 4.2

2. The $x$ -coordinate and $y$ -coordinate of the point where the line $x = - 2$ intersects the line $5 y - 3 x = - 9$ are ______ and ______, respectively.

−2; −3

Question 4.3

3. The $y$ -coordinate of the point whose $x$ value is 3 on the line $3 x + 2 y = 12$ is

3/2.
3.
2.

Question 4.4

4. The lines $x + 3 y = 12$ and $y = 3$ intersect at the point with $x$ -coordinate ______ and $y$ -coordinate ______.

3; 3

Question 4.5

5. The two lines $2 x + 3 y = 12$ and $6 x + 9 y = 7$

intersect at (3, 2).
intersect at (−3, −2).
are parallel.

Question 4.6

6. The $x$ -coordinate and $y$ -coordinate of the points where the line $7 x + 2 y = 28$ crosses the x-axis and y-axis, respectively, are ______ and ______.

14; 4

Question 4.7

7. Which of these points lie in the region $4 x + 3 y \geq 24, x \geq 0, y \geq 0$ ?

Points (2, 5) and (3, 4)
Points (5, 2) and (3, 4)
Points (5, 2) and (2, 5)

Page 162

Question 4.8

8. The difference between the set of those pairs $(x, y)$ that satisfy $x + 2 y < 8$ and $x + 2 y \leq 8$ is that the second inequality holds for points on the line _____, whereas the first inequality does not hold for points on this line.

$x + 2 y = 8$

Question 4.9

9. A tart requires 3 oz of fruit and 2 oz of dough; a pie requires 13 oz of fruit and 7 oz of dough. There are 140 oz of fruit and 90 oz of dough available. Each tart earns 6 cents profit; each pie earns 25 cents profit. The profit formula for this situation, if $x$ represents the numbers of pies produced and $y$ represents the number of tarts produced, is given by $P (i n c e n t s) =_____x +______y$ .

25; 6

Question 4.10

10. If the profit $P$ for making $x$ large and $y$ small shovels is $(P = 7 x + 6 y)$ , then the profit made if it were feasible to manufacture 6 small shovels and 8 large shovels would be ___________.

10.

Question 4.11

11. The cost $C$ of manufacturing $x$ pounds of flour blend $X$ and $y$ pounds of flour blend $Y$ is given as $C = 9 x + 4 y$ . If a company is using linear programming to minimize the cost of making the blends $X$ and $Y$ and this happens when $x = 11$ and $y = 9$ , which of the following statements must hold?

$x = 11$ and $y = 9$ cannot be an interior point of the feasible region.
$x = 11$ and $y$ = 9 cannot be a corner point.
$x = 11$ and $y = 9$ is the only point where the minimum can occur.

11.

Question 4.12

12. Producing a bench $(x)$ requires 3 boards, and producing a table $(y)$ requires 5 boards. There are 25 boards available. The resource constraint associated with this situation is $_____x +_____y \leq 25$ .

12.

3; 5

Question 4.13

13. For the feasible region of a linear-programming problem defined by the inequalities $x \geq 0, y \geq 0$ , and $2 x + 5 y \leq 10$ , which of the following pairs of points lies within the feasible region?

(5, 0) and (1/2, 2)
(0, 2) and (0, 0)
(2, 1) and (3, 1)

13.

Question 4.14

14. A tart requires 3 oz of fruit and 2 oz of dough; a pie requires 13 oz of fruit and 7 oz of dough. There are 140 oz of fruit and 90 oz of dough available. Each tart earns 6 cents profit; each pie earns 25 cents profit. What are the resource inequalities of this situation?

$\begin{array}{l} 3 x + 2 y \leq 140 \\ 13 x + 7 y \leq 90 \\ x \geq 0, y \geq 0 \end{array}$
$\begin{array}{l} 3 x + 13 y \leq 140 \\ 2 x + 7 y \leq 90 \\ x \geq 0, y \geq 0 \end{array}$
$\begin{array}{l} 3 x + 2 y \leq 6 \\ 13 x + 7 y \leq 25 \\ x \geq 0, y \geq 0 \end{array}$

14.

Question 4.15

15. Graph the feasible region identified by the following inequalities:

$\begin{array}{l} 2 x + 4 y \leq 20 \\ 4 x + 2 y \leq 16 \\ x \geq 0, y \geq 0 \end{array}$

Which of these points is not in the feasible region of the graph drawn?

(2, 4)
(5, 0)
(4, 0)

15.

Question 4.16

16. Suppose the feasible region has four corners, at points (0, 0), (5, 0), (0, 3), and (3, 2). If the profit formula is $$ 3 x - $ 2 y$ , the maximum value for the profit is ______________________.

16.

$15

Question 4.17

17. Suppose that the feasible region has four corners, at points (0, 0), (4, 0), (0, 3), and (3, 2). For which of these profit formulas is the profit maximized by producing a mix of products?

$$ x + $ 2 y$
$$ 2 x - $ 2 y$
$$ 2 x - $ y$

17.

Question 4.18

18. The corner point principle cannot be applied to find the optimal answer for the value of the profit $P = 3 x + 7 y$ , where the feasible region is shown in the diagram, because the feasible region is not _______________.

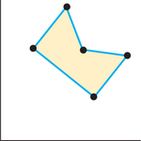
18.

convex

Question 4.19

19. The shaded region in the accompanying diagram is an example of a region

that is not convex.
that is not bounded by straight-line segments.
whose area is not bounded.

19.

Page 163

Question 4.20

20. Suppose that the feasible region has five corners, at points (1, 1), (2, 1), (3, 2), (2, 4), and (1, 5). Which of these points is not in the feasible region?

(1, 3)
(2, 2)
(0, 0)

20.

Question 4.21

21. Given the feasible region for a linear-programming problem defined by the inequalities $x \geq 0, y \geq 0$ , and $2 x + y \leq 12$ , the feasible point where $x = y$ with the largest possible $x$ -coordinate has $x$ -coordinate _____ and $y$ -coordinate _____.

21.

4; 4

Question 4.22

22. How does the line representing the maximum feasible profit intersect the feasible region?

There are no points of intersection.
There is only one point of intersection.
There is at least one point of intersection, and sometimes more than one point of intersection.

22.

Question 4.23

23. Consider the feasible region identified by the inequalities $x \geq 0, y \geq 0, 3 x + y \leq 10$ , and $x + 2 y \leq 6$ . The corner point of this region, which is not (0, 0), that has $x$ -coordinate 0 has $y$ -coordinate ___________.

23.

Question 4.24

24. Suppose the feasible region has five corners, at points (1, 1), (2, 1), (3, 2), (2, 4), and (1, 5). If the profit formula is $$ 5 x - $ 3 y$ , the corner point which maximizes the profit has $x$ -coordinate ____ and $y$ -coordinate ____.

24.

3; 2

Question 4.25

25. Consider the feasible region for a linear-programming problem involving the inequalities $x \geq 0, y \geq 0, 3 x + y \leq 10$ , and $x + 2 y \leq 5$ . The corner point for this feasible region that has no zero coordinates has $x$ -coordinate _____ and $y$ -coordinate _____.

25.

3; 1

Question 4.26

26. Given the feasible region for a linear-programming problem defined by the inequalities $x \geq 0, y \geq 0$ , and $2 x + y \leq 15$ , the feasible point where $x = y$ with the largest possible value for a $y$ -coordinate has coordinates

(5, 5).
(3, 3).
(0, 15).

26.

Question 4.27

27. When the Northwest Corner Rule is applied to the accompanying transportation problem tableau, the cells that remain empty are

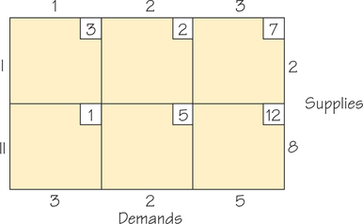
cell (I, 2) and cell (I, 3).
cell (II, 2) and cell (I, 2).
cell (I, 2) and cell (II, 3).

27.

Question 4.28

28. The circled cells in the accompanying tableau give a solution that satisfies the rim conditions. The cost associated with this solution is ____________.

28.

Question 4.29

29. The circled cells in the accompanying tableau satisfy the rim conditions. When the indicator value for cell (I, 2) is computed,

Page 164

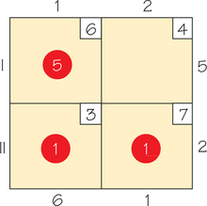
the result being negative, this tableau does not give a minimal cost solution.
the result being positive, this tableau has no minimal cost solution.
the result being positive, the current solution is optimal.

29.

Question 4.30

30. The indicator value associated with cell (I, 2) of the accompanying tableau is_________________.

30.

−3