Chapter 4 Exercises
Chapter 4 Exercises
4.1Linear Programming and Mixture Problems: Combining Resources to Maximize Profit
Question 4.31
1. Find the coordinates of all points where the lines x+y=8, y=5, and x=1 intersect.
1.
The intersection points are (1, 7), (1, 5), and (3, 5).
Question 4.32
2. Find the x- and y-intercepts of the line 6y+5x=30.
Question 4.33
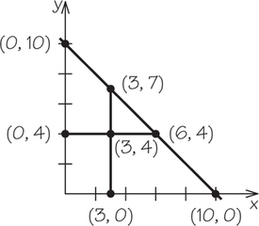
3. Graph the lines x+y=10, x=3, and y=4 on the same set of axes. For each pair of these three lines, find the x- and y-coordinates where the lines intersect.
3.
The lines x=3 and y=4 meet at the point (3, 4); the lines x=3 and x+y=10 meet at the point (3, 7); the lines y=4 and x+y+10 meet at the point (6, 4).
Question 4.34
4. Using intercepts, the points where the lines cross the axes, graph each line.
- 7x+6y=42
- x=2
- y=5
Question 4.35
5. Using intercepts, the points where the lines cross the axes, graph each line.
- 2x+3y=12
- 3x+5y=30
- 4x+3y=24
5.
(a)
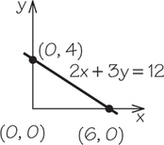
(b)
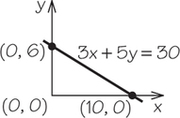
(c)
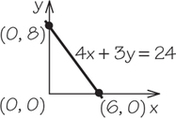
Question 4.36
6.
- Graph the lines x=2, y=3, x=4, and y=7 on the same set of axes.
- The points where the four lines meet form what kind of geometric figure (shape)?
Question 4.37
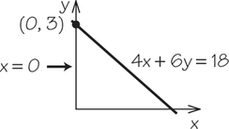
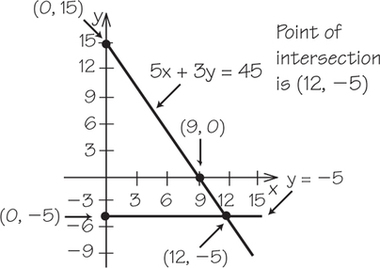
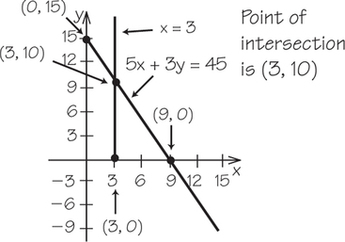
7. Graph both lines on the same axes. Put a dot where the lines intersect. Use algebra to find the x- and y-coordinates of the point of intersection.
- 4x+6y=18 and x=0
- 5x+3y=45 and y=−5
- 5x+3y=45 and x=3
7.
(a)
(b)
(c)
Note: For Exercises 9 and 11, first quadrant only is shown. Point of intersection is labeled.(b)5. (a)(b)
Question 4.38
8. Graph both lines on the same axes. Put a dot where the lines intersect. Use algebra to find the x- and y-coordinates of the point of intersection.
- x=3 and y=−2
- 3x+5y=45 and x=−5
- 5x+3y=45 and x=−3
Question 4.39
9. Graph both lines on the same axes. Put a dot where the lines intersect. Use algebra to find the x- and y-coordinates of the point of intersection.
- x+y=10 and x+2y=14
- y−2x=0 and x=2
9.
(a)
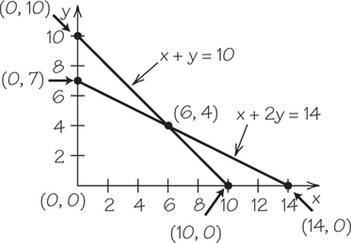
(b)
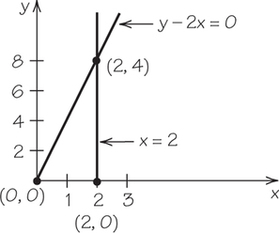
Question 4.40
10. Graph the line and half-plane corresponding to the inequality, a typical constraint from a mixture problem.
- x≥6
- y≥4
- 5x+3y≤15
- 4x+5y≤30
Question 4.41
11. Graph the line and half-plane corresponding to the inequality, a typical constraint from a mixture problem.
- x≥2
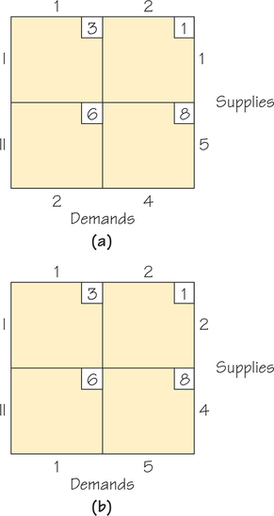
- y≥8
- 3x+2y≤18
- 7x+2y≤42
11.
(a)
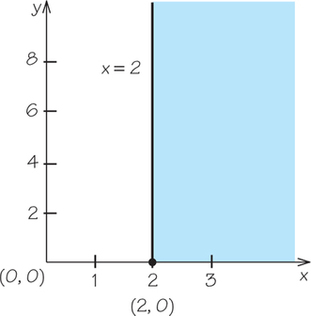
(b)
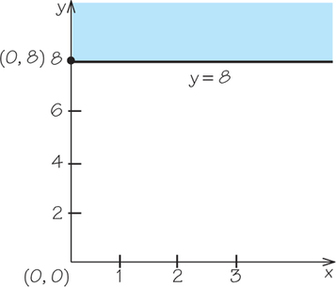
(c)
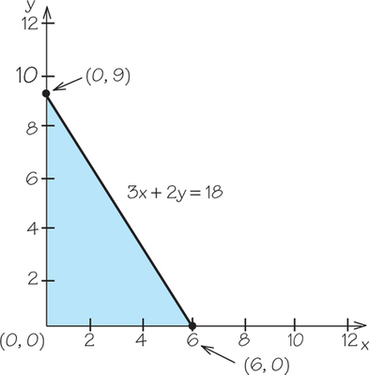
(d)
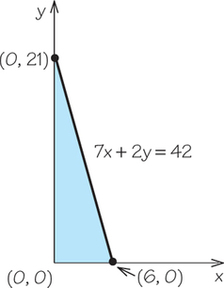
13.
(a) 6x+4y<300
(b) 30x+72y<420
For each description in Exercises 12–14, write one or more suitable resource-constraint inequalities. The unknown to use for each product is given in parentheses.
Question 4.42
12.
- One bridesmaid’s bouquet (x) requires 2 roses, and one corsage (y) requires 4 roses. There are 28 roses available.
- Maintaining a large tree (x) takes 1 hr of pruning time and 30 min of shredder time; maintaining a small tree (y) takes 30 min of pruning time and 15 min of shredder time. There are 40 hr of pruning time and 2 hr of shredder time available.
Question 4.43
13.
- Manufacturing one package of hot dogs (x) requires 6 oz of beef, and manufacturing one package of bologna (y) requires 4 oz of beef. There are 300 oz of beef available.
- It takes 30 ft of 12-in. board to make one bookcase (x); it takes 72 ft of 12-in. board to make one table (y). There are 420 ft of 12-in. board available.
13.
(a) 6x+4y≤300
(b) 30x+72y≤420
Question 4.44
14. Manufacturing one salami (x) requires 12 oz of beef and 4 oz of pork. Manufacturing one bologna (y) requires 10 oz of beef and 3 oz of pork. There are 40 lb of beef and 480 oz of pork available.
In Exercises 15–20, graph the feasible region, label each line segment bounding it with the appropriate equation, and give the coordinates of every corner point.
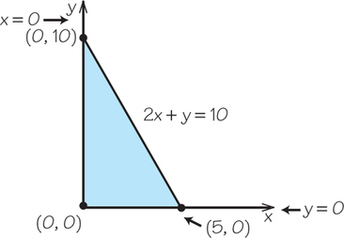
Question 4.45
15.x≥0; y≥0; 2x+y≤10
15.
Question 4.46
16.x≥0; y≥0; x+2y≤12; x+2y≤8
Question 4.47
17.x≥0; y≥0; 2x+5y≤60
17.
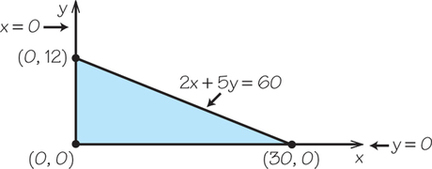
Question 4.48
18.x≥10; y≥0; 3x+5y≤120
Question 4.49
19.x≥0; y≥4; x+y≤20
19.
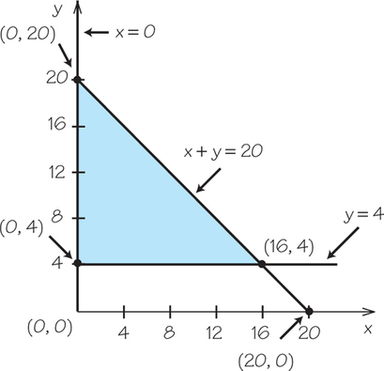
Question 4.50
20.x≥2; y≥6; 3x+2y≤30
In Exercises 21–22, determine whether the points (2, 4) and/or (10, 6) are points of the given feasible regions of:
Question 4.51
21. Exercises 15, 17, and 19.
21.
Exercise 15: (2, 4): yes; (10, 6): no; Exercise 17: (2, 4): yes; (10, 6): yes; Exercise 19: (2, 4): yes; (10, 6): yes
Question 4.52
22. Exercises 16, 18, and 20.
Question 4.53
23. In the toy problem, x represents the number of skateboards and y the number of dolls. Using the version of that problem whose feasible region is presented in Figure 4.3b, with the profit formula $2.30x+$3.70y, write a sentence giving the maximum profit and describing the production policy that gives that profit.
23.
Make 0 skateboards and 30 dolls for a profit of $111.
Question 4.54
24. In the toy problem, x represents the number of skateboards and y the number of dolls. Using the version of that problem whose feasible region is presented in Figure 4.3b, with the profit formula $5.50x+$1.80y, write a sentence giving the maximum profit and describing the production policy that gives that profit.
Question 4.55
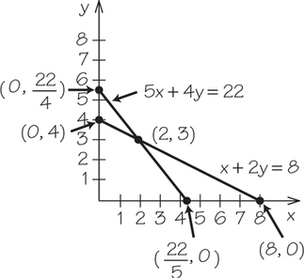
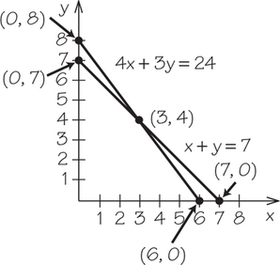
25. Graph both lines on the same axes. Put a dot where the lines intersect. Use algebra to find the x- and y-coordinates of the point of intersection.
- 5x+4y=22 and x+2y=8
- x+y=7 and 4x+3y=24
25.
Note: These situations are shown only for the first quadrant.
(a)
(b)
In Exercises 26–29, graph the feasible region, label each line segment bounding it with the appropriate equation, and give the coordinates of every corner point.
Question 4.56
26.x≥0; y≥0; 3x+y≤9; x+y≤7
Question 4.57
27.x≥0; y≥0; 2x+y≤4; 4x+4y≤12
27.
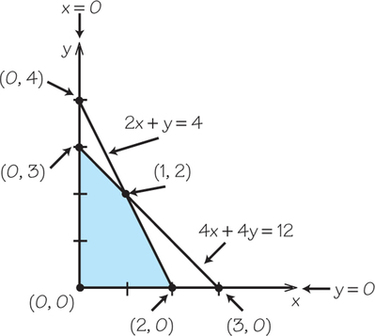
Question 4.58
28.x≥0; y≥2; 5x+y≤14; x+2y≤10
Question 4.59
29.x≥4; y≥0; 5x+4y≤60; x+y≤13
29.
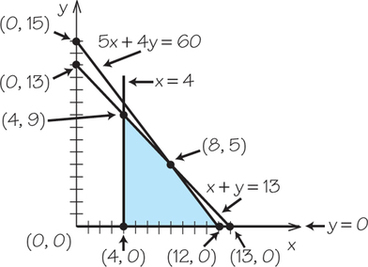
Question 4.60
30. Determine whether the points (4, 2) and/or (1, 3) are points of the given feasible regions of Exercises 27 and 29.
Question 4.61
31. Determine the maximum value of P given by P=3x+2y subject to the constraints x≥0, y≥0, x≤7, and y≤5.
31.
The maximum value of P is 31 and occurs at the point (7, 5).
Question 4.62
32. A linear-programming problem has constraints given by x≥0, y≥0, 5x−y≤15, and 4y+x≤24.
- What are the corner points of the feasible region for this LP problem?
- Sketch a graph of the feasible region.
4.2 Finding the Optimal Production Policy
4.3 Why the Corner Point Principle Works
4.4 Linear Programming: Life Is Complicated
Question 4.63
33. A linear-programming problem has constraints given by x>0, y>0, x<4, and 4y+13x≤60.
- Which, if any, of the constraints involve vertical and horizontal lines?
- Sketch a graph of the feasible region.
- What are the corner points of the feasible region?
- If profit is given by the expression P=3x+7y:
- What is the profit associated with the point (3, 1)?
- Which corner points have higher profit than (3, 1)?
33.
(a) x=0 and x=4 are vertical constraints, while y=0 is a horizontal constraint.
(b)
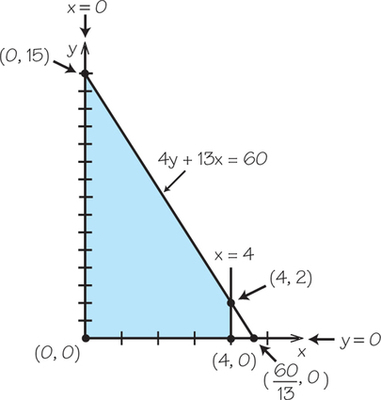
(c) (0, 0); (4, 0); (4, 2); (0, 15)
(d) (i) 16; (ii) (0, 15); (4, 2)
Question 4.64
34. Nuts Galore sells two spiced nut mixtures: Grade A and Grade B. Grade A requires 7 oz of peanuts for every 8 oz of almonds. Grade B requires 9 oz of peanuts for every 8 oz of almonds. There are 630 oz of peanuts and 640 oz of almonds available. Grade A makes Nuts Galore a profit of $1.70, and Grade B makes a profit of $2.40 per unit assembled. How many units of Grade A and Grade B nut mixtures should be made to maximize the company’s profit, assuming that all units made can be sold?
Question 4.65
35. Find the maximum value of P where P=3x+2y subject to the constraints x≥3, y≥2, x+y≤10, and 2x+3y≤24.
35.
28
Question 4.66
36. Find the maximum value of P where P=3x−2y subject to the constraints x≥2, y≥3, 3x+y≤18, and 6x+4y≤48.
Question 4.67
37. Find the maximum value of P where P=5x+2y subject to the constraints x>2, y>4, and x+y≤10.
37.
38
Question 4.68
38. Given profit P=21x+11y subject to the constraints x≥0,y≥0,7x+4y≤13:
- Graph the feasible region.
- Determine a corner point where there is an optimal solution. (Warning: The corner point where the optimal solution occurs may not have integer values for both x and y.)
Question 4.69
39.
- Referring to Exercise 38, use the usual rounding rule to round the x-coordinate and the y-coordinate of the point where the optimal linear-programming solution occurs. Call the point with these coordinates Q.
- Determine whether Q’s coordinates define a feasible point by checking them against the constraints.
- Evaluate the profit value P at point Q. How does the profit value compare with the point where the optimal value occurred in Exercise 38?
- Let R be the point with coordinates (0, 3). Is R in the feasible region? Evaluate P at point R and compare the result with the answer at Q and where the optimum linear-programming value occurred.
- Explain the significance of the situation here for solving maximization problems where P=ax+by (with a and b known in advance) is subject to linear constraints but where the variables must be nonnegative integers rather than arbitrary nonnegative decimal numbers.
39.
(a) (2, 0)
(b) They do not.
(c) Profit at (2, 0) is greater than the profit at (137,0).
(d) Yes; profit at R is less than the profit at Q.
(e) Answers will vary.
Exercises 40–51 each have several steps leading to a complete solution to a mixture problem. Practice a specific step of the solution algorithm by working out just that step for several problems. The steps are:
- Make a mixture chart for the problem.
- Using the mixture chart, write the profit formula and the resource- and minimum-constraint inequalities.
- Draw the feasible region for those constraints and find the coordinates of the corner points.
- Evaluate the profit information at the corner points to determine the production policy that best answers the question.
- (Requires technology) Compare your answer with the one you get from running the same problem on a simplex algorithm computer program.
Question 4.70
40. A clothing manufacturer has 600 yd of cloth available to make shirts and decorated vests. Each shirt requires 3 yd of material and provides a profit of $5. Each vest requires 2 yd of material and provides a profit of $2. The manufacturer wants to guarantee that under all circumstances, there are minimums of 100 shirts and 30 vests produced. How many of each garment should be made to maximize profit? If there are no minimum quantities, how, if at all, does the optimal production policy change?
Question 4.71
41. A car maintenance shop must decide how many oil changes and how many tune-ups can be scheduled in a typical week. The oil change takes 20 min, and the tune-up requires 100 min. The maintenance shop makes a profit of $15 on an oil change and $65 on a tune-up. What mix of services should the shop schedule if the typical week has 8000 min available for these two types of services? How, if at all, do the maximum profit and optimal production policy change if the shop is required to schedule at least 50 oil changes and 20 tune-ups?
41.
Schedule 400 oil changes and no tune-ups; schedule 300 oil changes and 20 tune-ups.
Question 4.72
42. A clerk in a bookstore has 90 min at the end of each workday to process orders received by mail or on voice mail. The store has found that a typical mail order brings in a profit of $30 and a typical voice-mail order brings in a profit of $40. Each mail order takes 10 min to process and each voice-mail order takes 15 min. How many of each type of order should the clerk process? How, if at all, do the maximum profit and optimal processing policy change if the clerk must process at least three mail orders and two voice-mail orders?
Question 4.73
43. In a certain medical office, a routine office visit requires 5 min of doctors’ time and a comprehensive office visit requires 25 min of doctors’ time. In a typical week, there are 1800 min of doctors’ time available. If the medical office clears $30 from a routine visit and $50 from a comprehensive visit, how many of each should be scheduled per week? How, if at all, do the maximum profit and optimal production policy change if the office is required to schedule at least 20 routine visits and 30 comprehensive ones?
43.
Schedule 360 routine visits and no comprehensive visits; schedule 210 routine visits and 30 comprehensive visits.
Question 4.74
44. A bakery makes 600 specialty breads—multigrain or herb—each week. Standing orders from restaurants are for 100 multigrain breads and 200 herb breads. The profit on each multigrain bread is $8 and on herb bread, $10. How many breads of each type should the bakery make to maximize profit? How, if at all, do the maximum profit and optimal production policy change if the bakery has no standing orders?
Question 4.75
45. A student has decided that passing a mathematics course will, in the long run, be twice as valuable as passing any other kind of course. The student estimates that passing a typical math course will require 12 hr a week to study and do homework. The student estimates that any other course will require only 8 hr a week. The student has 48 hr available for study per week. How many of each kind of course should the student take?
(Hint: The profit could be viewed as 2 “value points” for passing a math course and 1 “value point” for passing any other course.) How, if at all, do the maximum value and optimal course mix change if the student decides to take at least two math courses and two other courses?
Exercises 46–49 require finding the point of intersection of two lines, each corresponding to a resource constraint.
45.
Take four math courses and no other courses; take two math courses and two other courses.
Question 4.76
46. The firm WebsAreUs creates and maintains websites for client companies. There are two types of websites: “Hot” sites change their layout frequently but keep their content for long times; “cool” sites keep their layout for a while but frequently change their content. Maintaining a hot site requires 1.5 hr of layout time and 1 hr for content changes. Maintaining a cool site requires 1 hr of layout time and 2 hr for content changes. Every day, WebsAreUs has 12 hr available for layout changes and 16 hr for content changes. Net profit is $50 for a set of changes on a hot site and $250 for a set of changes on a cool site. To maximize profit, how many of each type of site should WebsAreUs maintain daily? How, if at all, do the maximum profit and optimal policy change if the company must maintain at least two hot and three cool sites daily?
Question 4.77
47. A paper recycling company uses scrap cloth and scrap paper to make two different grades of recycled paper. A single batch of grade A recycled paper is made from 25 lb of scrap cloth and 10 lb of scrap paper, whereas one batch of grade B recycled paper is made from 10 lb of scrap cloth and 20 lb of scrap paper. The company has 100 lb of scrap cloth and 120 lb of scrap paper on hand. A batch of grade A paper brings a profit of $500, whereas a batch of grade B paper brings a profit of $250. What amounts of each grade should be made? How, if at all, do the maximum profit and optimal production policy change if the company is required to produce at least one batch of each type?

47.
Make two grade A and five grade B batches in both cases.
Question 4.78
48. Jerry Wolfe has a 100-acre farm that he is dividing into one-acre plots, on each of which he builds a house. He then sells the house and land. It costs him $20,000 to build a modest house and $40,000 to build a deluxe house. He has $2,600,000 to cover these costs. The profits are $25,000 for a modest house and $60,000 for a deluxe house. How many of each type of house should he build to maximize profit? How, if at all, do the maximum profit and optimal production policy change if Wolfe is required to build at least 20 of each type of house?
Question 4.79
49. The maximum production of a soft-drink bottling company is 5000 cartons per day. The company produces regular and diet drinks and must make at least 600 cartons of regular and 1000 cartons of diet per day. Production costs are $1.00 per carton of regular and $1.20 per carton of diet. The daily operating budget is $5400. How many cartons of each type of drink should be produced if the profit is $0.10 per regular and $0.11 per diet? How, if at all, do the maximum profit and optimal bottling policy change if the company has no minimum required production?
49.
Make 3000 cartons of regular and 2000 cartons of diet in both cases.
Question 4.80
50. Wild Things raises pheasants and partridges to restock the woodlands and has room to raise 100 birds during the season. The cost of raising one bird is $20 per pheasant and $30 per partridge. The Wildlife Foundation pays Wild Things for the birds; the latter clears a profit of $14 per pheasant and $16 per partridge. Wild Things has $2400 available to cover costs. How many of each type of bird should they raise? How, if at all, do the maximum profit and optimal restocking policy change if Wild Things is required to raise at least 20 pheasants and 10 partridges?
Question 4.81
51. Lights Aglow makes desk lamps and floor lamps, on which the profits are $2.65 and $4.67, respectively. The company has 1200 hr of labor and $4200 for materials each week. A desk lamp takes 0.8 hr of labor and $4 for materials; a floor lamp takes 1.0 hr of labor and $3 for materials. What production policy maximizes profit? How, if at all, do the maximum profit and optimal production policy change if Lights Aglow wants to produce at least 150 desk lamps and 200 floor lamps per week?
51.
Make no desk lamps and 1200 floor lamps; make 150 desk lamps and 1080 floor lamps.
In Exercises 52–55, there are more than two products in the problem. Although you cannot solve these problems using the two-dimensional graphical method, you can follow these steps:
- Make a mixture chart for each problem.
- Using the mixture chart, write the resource- and minimum-constraint inequalities. Also write the profit formula.
- (Requires software) If you have a simplex method program available, run the program to obtain the optimal production policy.
Question 4.82
52. A toy company makes three types of toys, each of which must be processed by three machines: a shaper, a smoother, and a painter. Each Toy A requires 1 hr in the shaper, 2 hr in the smoother, and 1 hr in the painter, and brings in a $4 profit. Each Toy B requires 2 hr in the shaper, 1 hr in the smoother, and 3 hr in the painter, and brings in a $5 profit. Each Toy C requires 3 hr in the shaper, 2 hr in the smoother, and 1 hr in the painter, and brings in a $9 profit. The shaper can work at most 50 hr per week, the smoother 40 hr, and the painter 60 hr. What production policy would maximize the toy company’s profit?
Question 4.83
53. A rustic furniture company handcrafts chairs, tables, and beds. It has three workers, Chris, Sue, and Juan. Chris can work only 80 hr per month, but Sue and Juan can each put in 200 hr. Each of these artisans has special skills. To make a chair takes 1 hr of Chris’s time, 3 from Sue, and 2 from Juan. A table needs 3 hr from Chris, 5 from Sue, and 4 from Juan. A bed requires 5 hr from Chris, 4 from Sue, and 8 from Juan. Even artisans are concerned about maximizing their profit, so what product mix should the company stick with if it gets $100 profit per chair, $250 per table, and $350 per bed?
53.
Make 50 chairs, 10 tables, and no beds each month.
Question 4.84
54. A candy manufacturer has 1000 lb of chocolate, 200 lb of nuts, and 100 lb of fruit in stock. The Special Mix requires 3 lb of chocolate, 1 lb each of nuts and fruit, and it brings in $10. The Regular Mix requires 4 lb of chocolate, 0.5 lb of nuts, and no fruit, and brings in $6. The Purist Mix requires 5 lb of chocolate, no nuts or fruit, and brings in $4. How many boxes of each type should be produced to maximize profit?

Question 4.85
55. A gourmet coffee distributor has on hand 17,600 lb of African coffee, 21,120 oz of Brazilian coffee, and 12,320 oz of Colombian coffee. It sells four blends—Excellent, Southern, World, and Special—on which it makes these per-pound profits, respectively: $1.80, $1.40, $1.20, and $1.00. One pound of Excellent is 16 oz of Colombian; it is not a blend at all. One pound of Southern consists of 12 oz of Brazilian and 4 oz of Colombian. One pound of World requires 6 oz of African, 8 oz of Brazilian, and 2 oz of Colombian. One pound of Special is made up of 10 oz of African and 6 oz of Brazilian. What product mix should the gourmet coffee distributor prepare to maximize profit?
55.
Make 470 pounds of Excellent, none of Southern, 2400 pounds of World, and 320 pounds of Special.
In Exercises 56 and 57, use the fact that the corner point approach can also solve minimization problems to minimize the given expression for cost C.
Question 4.86
56. Minimize C given by C=7x+8y over the feasible region for Exercise 35.
Question 4.88
58. Show by example that a feasible region that has the nonnegativity constraints x≥0, y≥0, and x+y≤0.5 can have no feasible points with integer coordinates other than (0, 0).
Question 4.89
59. Courtesy Calls makes telephone calls for businesses and charities. A profit of $0.50 is made for each business call and $0.40 for each charity call. It takes 4 min (on average) to make a business call and 6 min (on average) to make a charity call. If there are 240 min of calling time to be distributed each day, how should that time be spent so that Courtesy Calls makes a maximum profit? What changes, if any, occur in the maximum profit and optimal production policy if they must make at least 12 business and 10 charity calls every day?
59.
Make 60 business and no charity calls; make 45 business and 10 charity calls.
Question 4.90
60. A refinery mixes high-octane and low-octane fuels to produce regular and premium gasolines. The profits per gallon on the two gasolines are $0.30 and $0.40, respectively. One gallon of premium gasoline is produced by mixing 0.5 gal of each of the fuels. One gallon of regular gasoline is produced by mixing 0. 25 gal of high octane with 0.75 gal of low octane. If there are 500 gal of high octane and 600 gal of low octane available, how many gallons of each gasoline should the refinery make? How, if at all, do the maximum profit and optimal production policy change if the refinery is required to produce at least 100 gal of each gasoline?
Question 4.91
61. A toy manufacturer makes bikes, for a profit of $12, and wagons, for a profit of $10. To produce a bike requires 2 hr of machine time and 4 hr painting time. To produce a wagon requires 3 hr machine time and 2 hr painting time. There are 12 hr of machine time and 16 hr of painting time available per day. How many of each toy should be produced to maximize profit? How, if at all, do the maximum profit and optimal production policy change if the manufacturer must produce at least two bikes and two wagons daily?
61.
Make 3 bikes and 2 wagons in both cases.
4.5 A Transportation Problem: Delivering Perishables
4.6 Improving on the Current Solution
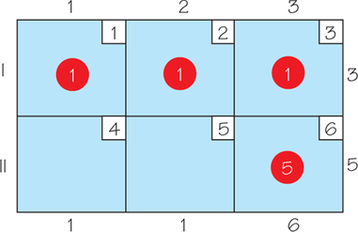
Question 4.92
62. Apply the Northwest Corner Rule, thereby finding a feasible solution that obeys the rim conditions, to the following transportation problem tableaux.
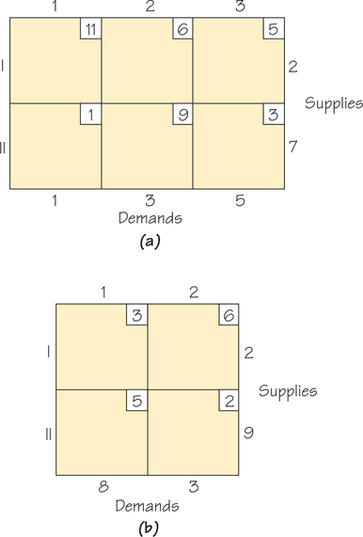
- For each tableau, give a possible real-world setting for the problem.
- For each tableau, find the cost of shipping using the cells that were circled when you applied the Northwest Corner Rule.
Question 4.93
63. The accompanying tableau represents the shipping costs and supply-and-demand constraints for supplies of purified water to be shipped to companies that resell the water to office buildings.
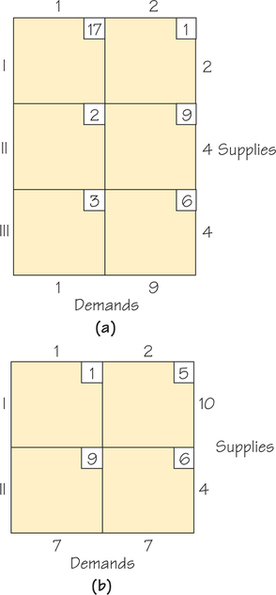
- For each tableau, give a possible real-world setting for the problem.
- For each tableau, find the cost of shipping using the cells that were circled when you used the Northwest Corner Rule.
63.
(a)
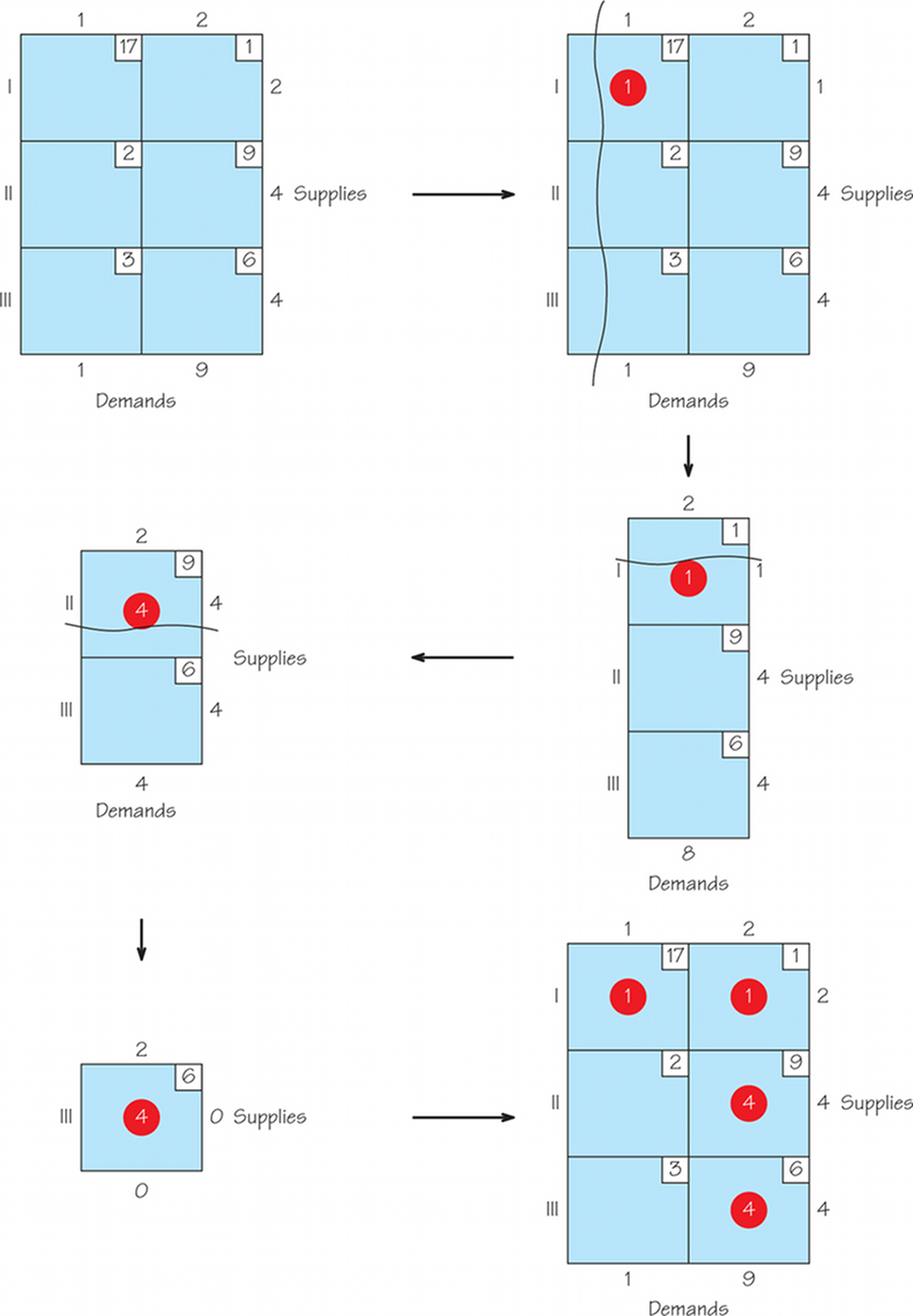
(b)
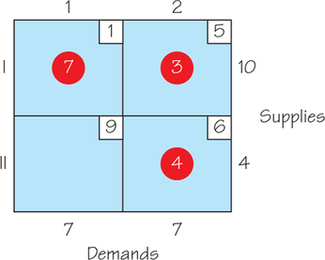
(c) This tableau could represent how to meet the needs of two organic groceries with organic fruit from two suppliers.
(d) The cost associated with this way to ship is 46.
Question 4.94
64. The accompanying tableau represents the shipping costs and supply-and-demand constraints for supplies of purified water to be shipped to companies that resell the water to office buildings.
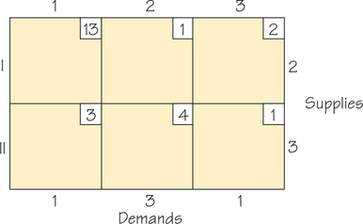
- Find the Northwest Corner Rule initial solution.
- Determine the indicator value for each noncircled cell.
- Is the current solution optimal? If not, find a cheaper solution.
Question 4.95
65.
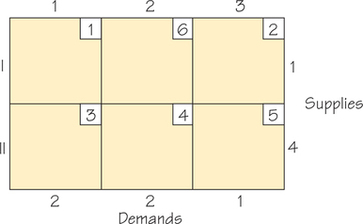
- Apply the Northwest Corner Rule, thereby finding a feasible solution that obeys the rim conditions, to the accompanying tableau which arose from meeting the demands of fruit stands for peaches from supplies available from local orchards.
- Determine the cost associated with the solution that you found.
- Compute the indicator value for each noncircled cell.
65.
(a)
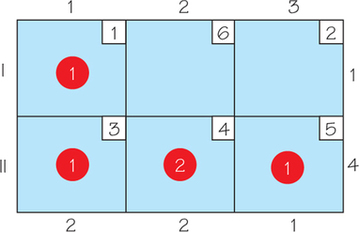
(b) 17
(c) (I, 2): 4; (I, 3): −1
Question 4.96
66. Apply the Northwest Corner Rule, thereby finding a feasible solution that obeys the rim conditions for the following transportation problem diagrams.
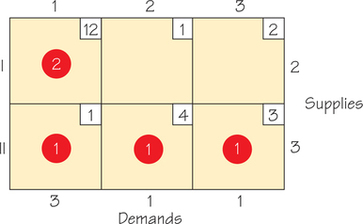
- For each diagram, give a possible real-world setting for the problem.
- For each diagram, find the cost of shipping using the cells that were circled when you applied the Northwest Corner Rule.
- Can you describe how the two diagrams are related?
- Compare the cost of the Northwest Corner feasible solutions you found for each of these two situations. Are you surprised by what you found?
Question 4.97
67. The accompanying tableau arose by applying the Northwest Corner Rule.
The accompanying graph was constructed so that there is one edge for each circled vertex in the tableau above.
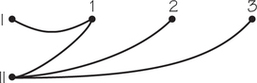
- Verify that the graph is a tree.
- Show that for each empty cell in the tableau, adding to the graph the unique edge that corresponds to the empty cell creates one circuit.
- Show that this circuit corresponds to the one that is used to find the indicator value of the empty cell.
67.
(a) Connected and has no circuit
(b) Add edge joining vertex I to vertex 2; add edge from vertex I to vertex 3.
(c) Circuit 2, I, 1, II, 2 corresponds to the circuit of cells, (I, 2), (I, 1), (II, 1), (II, 2), (I, 2). Circuit 3, I, 1, II, 3 corresponds to the circuit of cells, (I, 3), (I, 1), (II, 1), (II, 3), (I, 3).
Question 4.98
68.
- For each row of the following tableau, compute the minimum cost for that row. Now select the row R that among all the rows has the smallest row minimum. In a way similar to the Northwest Corner Rule, use the cheapest cell in row R and ship as much as possible via that cell, crossing out a row or a column, and adjust the rim conditions and repeat the process. This is known as the minimum row entry method. Use the minimum row entry method to find an initial solution to the following transportation problem, which shows the costs of returning rental cars from cities that have more cars than necessary to cities that have too few cars.
- Compute the cost of the solution you find using the minimum row entry method.
- Compare the cost found in part (b) with the cost of the initial solution obtained using the Northwest Corner Rule.
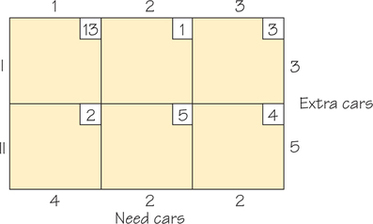
Question 4.99
69.
- For each of the following tableaux, find an initial solution using the Northwest Corner Rule.
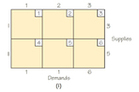
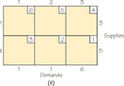
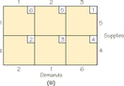
- If the solution you find using the Northwest Corner Rule is not optimal, then apply the stepping stone algorithm to find an optimal solution.
69.
(a) (i)
(ii)
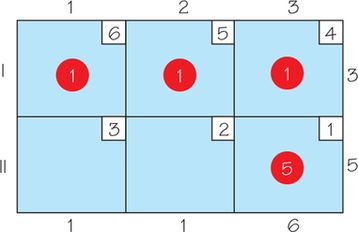
(iii)
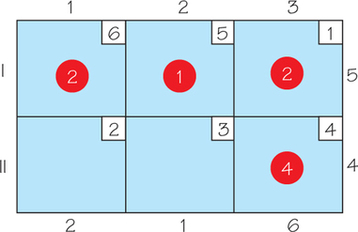
(b) For both (i) and (ii) the tableaux shown are optimal. However, there are also other optimal tableaux. For (iii) the tableau shown is not optimal. Using the stepping stone algorithm, the cost can be reduced to 16.
Question 4.100
70.
- Apply the Northwest Corner Rule to the following tableau.
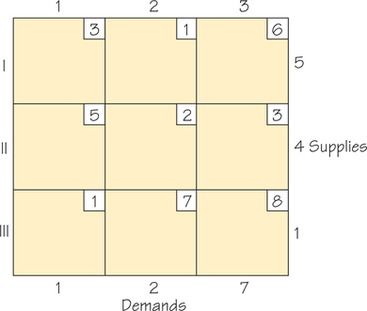
- Determine the cost associated with the solution you found.
- Compute the indicator value for each noncircled cell.
- Does the Northwest Corner Rule give rise to an optimal solution?
Question 4.101
71. For each of the situations below, explain whether it seems reasonable to try to model it as a transportation problem.
- A supermarket chain is arranging to control costs in supplying the delivery of vegetables from its suppliers to its many branch stores.
- A mining company is trying to control the costs of repaving the roads that form the road network within the mine premises.
- A company is operating oil refineries to produce gasoline, as well as gasoline stations, to keep the cost of gasoline at the pump down.
71.
(a) Yes
(b) No
(c) Yes
Question 4.102
72. Apply the Northwest Corner Rule to find a feasible solution for the transportation problem given in the accompanying tableau, and find the cost of shipping using this feasible solution (circled cells).
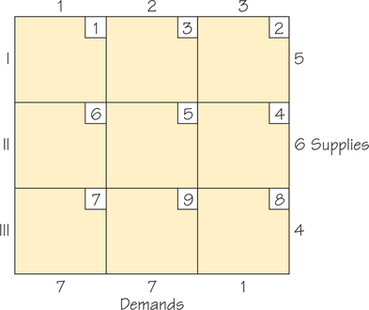
Question 4.103
73.
- We developed a Northwest Corner Rule to find a feasible solution to a transportation problem. Can you formulate a Southeast Corner Rule to find a feasible solution to a transportation problem by reasoning in an analogous way to how we developed the Northwest Corner Rule?
- Apply your Southeast Corner Rule to the tableau in Exercise 72. Compare the costs of the feasible solutions that resulted from using the two different rules.
- What are the pros and cons of the Southeast Corner Rule compared with the Northwest Corner Rule?
73.
(a) The cost associated with the feasible solution shown is 72.
(b)
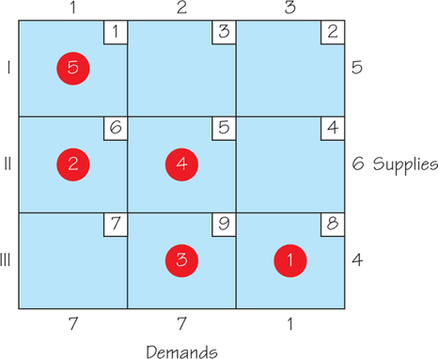
The cost associated with the feasible solution obtained is the same as for the Northwest Corner Rule. However, this will not always be true.
(c) Answers will vary.
Chapter Review
Question 4.104
74. Graph on the same set of axes the equations x=3, y=5, and 2x+3y=17. In the diagram:
- Indicate the points at which the lines cut the coordinate axes.
- Indicate the points of intersection of the three lines.
Question 4.105
75. If maximal profit is given by P=3x+5y, what is the maximal value of P for the constraints x≥0, y≥0, x≥3, y≥7, and x+y<11?
75.
49
Question 4.106
76. Two dairies supply three supermarket chains with the demands for milk, as shown in the table below. Also indicated in a cell is the cost of shipping between pairs of sites.
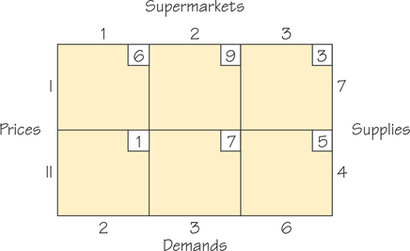
- Use the Northwest Corner Rule to obtain a feasible solution.
- If the feasible solution in part (a) is not an optimal one, find an optimal solution.
