4.5 4.4 Linear Programming: Life Is Complicated
Every algorithm for solving a linear-programming problem has the following three characteristics, which hold true regardless of the number of products or the number of resources in the problem:
- The algorithm can distinguish between “good” production policies—those in the feasible set that satisfy all the constraints—and those that violate some constraint(s) and are thus not feasible. There are usually many good points, each of which corresponds to some production policy; for example, “Make x units of product 1 and y units of product 2.”
- The algorithm uses some geometric principles—one of which is the corner point principle—to select a special subset of the feasible set.
- The algorithm evaluates the profit formula at points in the special subset to find which corner point actually gives the maximum profit.
The various algorithms for linear programming differ in how they process the feasible set and in how quickly the algorithm finds the production policy—corner point—that gives the optimal profit.
In practical linear-programming problems, the feasible region will not be as simple as the ones we have examined here. There are two ways the feasible region can be more complex:
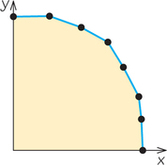
- Sometimes, as in Figure 4.14, we have a great many corners. The more corners there are, the more calculations we need to determine the coordinates of all of them and the profit at each one. The number of corners literally can exceed the number of grains of sand on the earth. Even with the fastest computer, computing the profit of every corner is impossible.
- It is not possible to visualize the feasible region as a part of two-dimensional space when there are more than two products. Each product is represented by an unknown, and each unknown is represented by a dimension of space. If we have 50 products, we would need 50 dimensions and couldn’t visualize the feasible region.
Another type of complication can occur even in simple two-dimensional regions: Corner points can have fractional coordinates, not the integer ones we see in the specially constructed problems in this text. Making 3.75 skateboards and 5.45 dolls is not possible. As mentioned earlier, integer programming, a special type of linear programming, is used when it is not realistic to use fractional answers.
We have looked at some simple mixture problems to illustrate the power of linear programming to solve optimization problems. Solving similar problems scaled up to a realistic level is widely applied by governments, businesses, and humanitarian organizations to make the world a better place that runs more smoothly.
The Simplex Method
Several methods are used for the typically large linear-programming problems solved in practice. The oldest method is the simplex method, which is still the most commonly used. Devised by the American mathematician George Dantzig (see Spotlight 4.2 on page 146), this ingenious mathematical invention makes it possible to find the best corner point by evaluating only a tiny fraction of all the corners. With the use of the simplex method, a problem that might be impossible to solve if each corner point had to be checked can be solved in a few minutes or even a few seconds on a typical business computer.
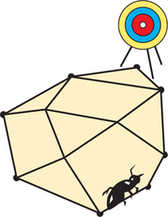
The operation of the simplex method may be likened to the behavior of an ant crawling on the edges of a polyhedron (a solid with flat sides) looking for an optimal corner point—one that gives the highest profit (Figure 4.15). The ant cannot see where the optimal corner is. As a result, if it were to wander along the edges randomly, it might take a long time to reach that corner. The ant will do much better if it has a temperature clue to let it know it is getting warmer (closer to the optimal corner) or colder (farther from the optimal corner).
Think of the simplex method as a way of calculating these temperature hints. We begin at any corner. All neighboring corners are evaluated to see which ones are warmer and which are colder. A new corner is chosen from among the warmer ones, and the evaluation of neighbors is repeated—this time checking neighbors of the new corner. The process ends when we arrive at a corner point, all of whose neighbors are colder than it is.
Part of what the simplex method has going for it is that it works faster in practice than its worst-case behavior would lead us to believe. Although mathematicians have devised artificial cases for which the simplex method bogs down in unacceptable amounts of arithmetic, the examples arising from real applications are never like that. This may be the world’s most impressive counterexample to Murphy’s law, which says that if something can go wrong, it will.
Although the simplex method usually avoids visiting every corner, it may require visiting many intermediate ones as it moves from the starting corner to the optimal one. The simplex method has to search along edges on the boundary of the polyhedron. If it happens that there are a great many small edges lying between the starting corner and the optimal one, the simplex method must operate like a slow-moving bus that stops on every block.
Many computer programs are available that will use the simplex method to produce an optimal production policy if we just supply the computer with the constraint inequalities and profit formula. Simplex method programs can be found in a variety of places, including electronic spreadsheets, packages of mathematics programs designed for business applications or finite mathematics courses, and large “all-purpose” mathematics packages. A graphical solution is possible only for problems limited to two products; these special exercises involve more than two products.
The Father of Linear Programming Recalls Its Origins 4.2
4.2
George Dantzig, who died in 2005, spent most of his career as a professor of operations research and computer science at Stanford University. He is credited with inventing the linear-programming technique called the simplex method. Since its invention in the 1940s, the simplex method has provided solutions to linear-programming problems that have saved both industry and the military time and money. Here Dantzig talks about the background of his famous technique:
Initially, all the work we did had to do with military planning. During World War ii, we were planning on a very extensive scale. The civilian population and the military were all performing scheduling and planning tasks, perhaps on a larger scale than at any time in history. And this was the case up until about 1950. From 1950 on, the whole emphasis shifted from military planning to practical planning for the civilian population, and industry picked it up.
The first areas of industry to use linear programming were the petroleum refineries. They used it for blending gasoline. Nowadays, all of the refineries in the world (except for one) use linear-programming methods. They are one of the biggest users of it, and it’s been picked up by every other industry you can think of—the forestry industry, the steel industry. You could fill up a book with all the different places it’s used.
The question of why linear programming wasn’t invented before World War ii is an interesting one. in the postwar period, various technologies just evolved that had never been there before. Computers were one example. These technologies were talked about before. You can go back in history and you’ll find papers on them, but these were isolated cases that never went anywhere….
The problems we solve nowadays have thousands of equations, sometimes a million variables. One of the things that still amazes me is to see a program run on the computer—and to see the answer come out. if we think of the number of combinations of different solutions that we’re trying to choose the best of, it’s akin to the stars in the heavens. Yet we solve them in a matter of moments. This, to me, is staggering. Not that we can solve them—but that we can solve them so rapidly and efficiently.

The simplex method has been used now for roughly 70 years. There has been steady work going on trying to use different versions of the simplex method, nonlinear methods, and interior methods. it has been recognized that certain classes of problems can be solved much more rapidly by special algorithms than by using the simplex method. if i were to say what my field of specialty is, it is in looking at these different methods and seeing which are more promising than others. There’s a lot of promise in this—there’s always something new to be looked at.
An Alternative to the Simplex Method
In 1984, Narendra Karmarkar, a mathematician working at AT&T Bell Laboratories, devised an alternative method for linear programming that finds the optimal corner point in fewer steps than the simplex algorithm by making use of search routes through the interior of the feasible region. The applications of Karmarkar’s algorithm are important to a lot of industries, including telephone communications and the airlines (see Spotlight 4.3). Routing millions of long-distance calls, for example, means deciding how to use the resources of long-distance landlines, repeater amplifiers, and satellite terminals to best advantage. The problem is similar to the juice company’s need to find the best use of its stocks of juice to create the most profitable mix of products.
Finding Fast Algorithms Means Better Airline Service 4.3
4.3
Linear-programming techniques have a direct impact on the efficiency and profitability of major airlines. Thomas Cook, once director of operations research at American Airlines, made these comments concerning why optimal solutions are essential to the airline business:
Finding an optimal solution means finding the best solution. Let’s say you are trying to minimize a cost function of some kind. For example, we may want to minimize the excess costs related to scheduling crews, hotels, and other costs that are not associated with flight time. So we try to minimize that excess cost, subject to a lot of constraints, such as the amount of time a pilot can fly, how much rest time is needed, and so forth.
An optimal solution, then, is either a minimum- cost solution or a maximizing solution. For example, we might want to maximize the profit associated with assigning aircrafts to the schedule; so we assign large aircraft to high-need segments and small aircraft to low-load segments.
The simplex method, which was developed some 50 years ago by George Dantzig, has been very useful at American Airlines and, indeed, at a lot of large businesses. The difference between his method and Narendra Karmarkar’s is speed. Finding fast solutions to linear-programming problems is also essential. With an algorithm like Karmarkar’s, which is 50 to 100 times faster than the simplex method, we could do a lot of things that we couldn’t do otherwise. For example, some applications could be real-time applications, as opposed to batch applications. So instead of running a job overnight and getting an answer the next morning, we could actually key in the data or access the database, generate the matrix, and come up with a solution that could be implemented a few minutes after keying in the data.
A good example of this kind of application is what we call a major weather disruption. if we get a major weather disruption at one of the hubs, such as Dallas or Chicago, then a lot of flights may get canceled, which means we have a lot of crews and airplanes in the wrong places. What we need is a way to put that whole operation back together again so that the crews and airplanes are in the right places. That way, we minimize the cost of the disruption, as well as passenger inconvenience.
Many airlines use software based on Karmarkar’s algorithm to reduce fuel costs and deal with delays caused by storms.

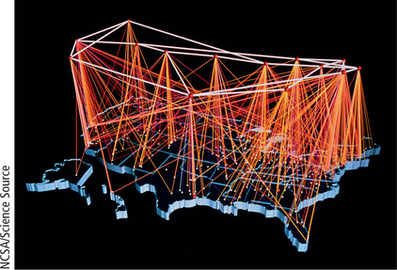
In the 1980s, scientists at Bell Labs applied Karmarkar’s algorithm to a problem of unprecedented complexity: deciding how to economically build telephone links between cities so that calls can get from any city to any other, possibly being relayed through intermediate cities. Figure 4.16 shows a graph theory model (with color coding to show the intensity of traffic) for a portion of the Internet as it existed in the 1990s. Now, the number of ways to route Internet traffic has become unimaginably large, so picking the most efficient way to route email or other data packages is very difficult without using OR techniques.
Now that cell phones and Internet phone services are increasingly being used instead of landlines, new kinds of linear- and integer-programming problems and solutions have emerged to help provide better communications services. A typical example is using linear programming to determine the optimal locations for cell phone tower placement to achieve the best service. Integer programming is also being used to improve Wi-Fi and sensor network service.