In Example 4 (page 251), we used the straight line given by the equation

to predict BAC from the number of beers consumed. How did we get this particular equation? What makes it the equation of the “best-fitting” line for predicting BAC from beers consumed? Before we can answer the first question, we will first have to decide what we mean by the “best line.”

For a given scatterplot, different people might draw different summarizing lines by eye. For example, Figure 6.13 shows a scatterplot of the BAC-beer data along with three lines. Line 3 is the graph of the equation in the previous paragraph.

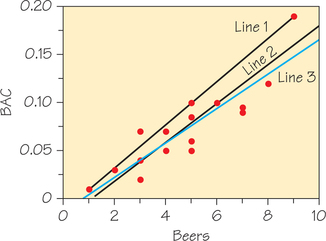
Line 1 was drawn through the points corresponding to the fewest and most beers consumed, (1, 0.01) and (9, 0.19). Line 2 was drawn through the points (3, 0.04) and (6, 0.10). So how do you determine which is the “best” line? If the criterion for the “best” line is the line passing through the most data points, Line 1 (which passes through three data points) would be the best, and Line 3 (which passes through one data point) the worst. However, Line 1 does a poor job of summarizing the overall pattern of these data. Only one data point lies above Line 1 and the rest lie on or below it. So picking a line that passes through the most data points is clearly a poor criterion for selecting a “best-fitting” line.

In looking for a new criterion for a “best” line, keep in mind that we will use this line to predict $y$ from $x$. Thus, we want a line that is as close as possible to the points in the vertical dimension. That’s because the prediction errors that we make are errors in the $y$-variable, which is the vertical dimension in the scatterplot.

Table 6.1 (page 243) shows that Student 12 drank 6 beers and was observed to have a BAC of 0.10. However, the regression-line equation in Example 4 showed that the predicted BAC for a student who drinks 6 beers is 0.095. These values are close, but not the same. Indeed, from Figure 6.6, we can see that the observed data point (6, 0.10) lies a bit above the line. The vertical deviation of this gap is the residual error (or simply residual), which is calculated as follows:

When the observed response lies above the line (e.g., the data point for Student 1, who had 5 beers and a BAC of 0.10, lies above Line 3 in Figure 6.13), the residual is positive. And when the response lies below the line (e.g., the data point for Student 14, who had 7 beers and a BAC of 0.09, lies below Line 3), the residual is negative. Figure 6.14 shows a graphical representation of these two residuals, the vertical gaps between these data points and the line.

Self Check 7

Now, we return to the problem of picking a “best” line. The most common way to make the collection of residual errors for the entire dataset as small as possible is least-squares regression. Line 3 in Figure 6.13 is the least-squares regression line.

So we now have a criterion for finding the “best-fitting” line—find the line that results in the smallest sum of the squares of the residual errors. Lines 2 and 3 in Figure 6.13 both appear to be good choices for this line. With a modest amount of algebra, we determined an equation for Line 2:

Using Excel, we then calculated the predicted values, residuals, and squares of the residuals, which are shown in Table 6.6. At the bottom of the last column of Table 6.6 is the sum of the squares of the residuals, which for Line 2 is 0.00625—a fairly small value. We then did the same calculations for Line 3: predicted $\text{BAC}=-0.0127+0.01796\times \text{beers}$, and found that the sum of the squares of the residuals was even smaller, 0.00585. So, based on the least-squares criterion, Line 3 is better than Line 2.

We can use the least-squares criterion for deciding which of two lines fits the data better. However, we still need a solution to the following mathematical problem: Starting with $n$ observations on variables $x$ and $y$, find the line that makes the sum of the squares of the vertical errors (the residuals) as small as possible. Here is the solution to this problem.

This equation gives insight into the behavior of least-squares regression by showing that it is related to the means and standard deviations of the $x$ and $y$ observations and to the correlation between $x$ and $y$. For example, it is clear that the slope $m$ always has the same sign as the correlation $r$.

In practice, you don’t need to calculate the means, standard deviations, and correlation first. Statistical software, spreadsheet software, and many calculators can give the slope $m$, intercept $b$, and equation of the least-squares line from keyed-in values of the variables $x$ and $y$ (see Spotlight 6.5 on page 266).

Self Check 8

You now see that correlation and least-squares regression are connected closely. The expression $m=r{s}_y/s_x$ for the slope says that along the regression line, a change of 1 standard deviation in $x$ corresponds to a change of $r$ standard deviations in $y$. When the variables are correlated perfectly ($r=1$ or $r=-1$), the change in the predicted $y$ is the same (in standard deviation units) as the change in $x$. Otherwise, because $-1\le r\le 1$, the change in the predicted $y$ is less than the change in $x$.

Now that we’ve covered both correlation and regression, check out Spotlight 6.4, which discusses how colleges might use regression and correlation in their admissions process.

Regression and Correlation in Action: College Success 6.4

Although the procedure box for calculating the equation of the least-squares regression line provides valuable insight about the line, it is extremely time consuming to compute that equation without the use of technology. Spotlight 6.5 gives instructions for using technology to calculate the regression equation.

Calculating the Equation of the Least-Squares Regression Line 6.5

Finally, technology comes to the rescue!

If you have a scientific calculator, select the calculator mode to be able to do two-variable regression statistics, clear out any old data, and then enter your new $x$- and $y$-values. Once the data are entered, you can find the regression-line slope and $y$-intercept by hitting the appropriate key(s). On the Internet, you can find websites that will help with the keystrokes for specific calculator models.

Page 266

TI-83/841 Family and Other TI Graphing Calculators

You can use your graphing calculator to compute the coefficients of the least-squares regression line and the correlation, make a scatterplot of the data, and overlay a graph of the least-squares regression line. We use the data on midterm and final exam scores from Table 6.2 (page 244) as an example.

• Step 1. Preparation
  • Turn off all STAT PLOTS:$\begin{array}{||}\hline \text{2nd}\\ \hline\end{array}$ $\begin{array}{||}\hline \text{Y=}\\ \hline\end{array}$ (for STAT PLOT) $\begin{array}{||}\hline 4\\ \hline\end{array}$ $\begin{array}{||}\hline \text{ENTER}\\ \hline\end{array}$.
  • Press $\begin{array}{||}\hline \text{Y}=\\ \hline\end{array}$ and erase (or turn off) any functions stored in the $\text{Y}=\text{menu}$.
  • Turn on Diagnostics: $\begin{array}{||}\hline \text{2nd}\\ \hline\end{array}$ $\begin{array}{||}\hline 0\\ \hline\end{array}$ (for CATALOG). Press $\begin{array}{||}\hline x^{-1}\\ \hline\end{array}$ (for D) to scroll to the Ds. Then use the down arrow key to scroll to DiagnosticOn. Press $\begin{array}{||}\hline \text{ENTER}\\ \hline\end{array}$ twice. (Your calculator should respond “Done.”)
  • Press $\begin{array}{||}\hline \text{STAT}\\ \hline\end{array}$ $\begin{array}{||}\hline 1\\ \hline\end{array}$. Clear any data from lists L1 and L2.

• Step 2. Determining the equation of the least-squares line and correlation

  • You should still be in the lists from Step 1. Enter the data on the explanatory variable, midterm exam scores, in list L1, and the response variable, final exam scores, in list L2 (be sure not to interchange these lists).
  • To calculate the coefficients of the least-squares regression line and the correlation:
    • Press $\begin{array}{||}\hline \text{STAT}\\ \hline\end{array}$ → CALC → LinReg($\text{ax}+\text{b}$), and then $\begin{array}{||}\hline \text{ENTER}\\ \hline\end{array}$.
      
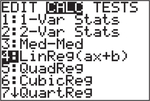
    • Complete the command as follows: $\begin{array}{||}\hline 2\text{nd}\\ \hline\end{array}$ $\begin{array}{||}\hline 1\\ \hline\end{array}$ (for L1)$\begin{array}{||}\hline ,\\ \hline\end{array}$ VARS → Y-VARS → Function, and then press $\begin{array}{||}\hline \text{ENTER}\\ \hline\end{array}$ ].
    • Press $\begin{array}{||}\hline 1\\ \hline\end{array}$ to store the equation as Y1 and then $\begin{array}{||}\hline \text{ENTER}\\ \hline\end{array}$.
  • Read off the coefficients of the line $y=ax+b$. (Notice that the slope is designated as $a$ and the $y$-intercept as $b$.) The correlation $r$ appears at the bottom of the screen.
    

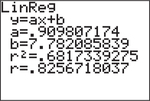
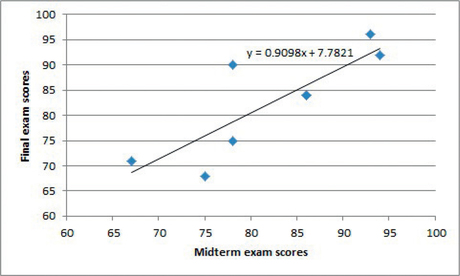
  You can put the equation together by substituting the values for $a$ and $b$ to get $\bar{y}=0.909807174x+7.782085839$.

• Step 3. Making a scatterplot and graphing the least- squares line
  • Press $\begin{array}{||}\hline 2\text{nd}\\ \hline\end{array}$ $\begin{array}{||}\hline \text{Y=}\\ \hline\end{array}$ (for STAT PLOT) $\begin{array}{||}\hline 1\\ \hline\end{array}$ $\begin{array}{||}\hline \text{ENTER}\\ \hline\end{array}$ to turn on STATPLOT 1.
  • For TYPE, select the first scatterplot; L1 and L2 should be entered as the Xlist and Ylist, respectively; choose the mark to be used for the dots in the scatterplot.
    
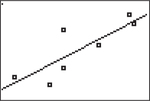
  • Press $\begin{array}{||}\hline \text{ZOOM}\\ \hline\end{array}$ $\begin{array}{||}\hline 9\\ \hline\end{array}$] (for ZoomStat).
    
• Step 4. After completing this problem, turn off all STAT PLOTS.

Keystrokes for other specific TI graphing calculators can be found online in the Texas Instruments guidebooks, which are downloadable from education.ti.com/calculators/downloads/US/#Guidebooks.

Page 267

Excel

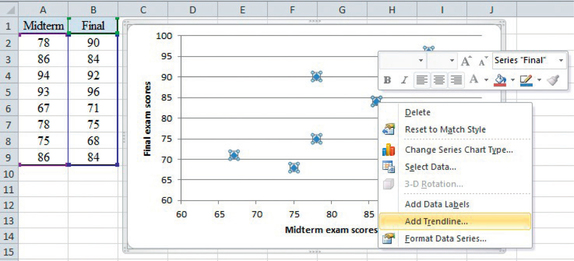
Again, we use the data from Table 6.2. The process will be to make a scatterplot of final exam scores against midterm exam scores and then to fit a line to the data.

• Enter the $x$-data, midterm exam scores, in column A and the $y$-data, final exam scores, in column B. (Don’t interchange the order of the columns.)
• Highlight your data by clicking at the top of column A, dragging over to the top of column B, and then down to the bottom of column B.
• Click the Insert tab and then the Scatter tab. Select the first scatterplot (Scatter with only Markers). You should now see a scatterplot of the data. Adjust the scaling for the axes so that the minimum for both the $x$- and $y$-axes is 60 (see Spotlight 6.1 on page 249).
• Next, right click on a dot in the scatterplot and select Add Trendline.
• Notice that Linear is selected by default. At the bottom, click the box opposite “Display Equation on chart.” Then click Close. A graph of the least- squares regression line along with its equation will be added to the scatterplot.