Algebra Review II: Representing Numbers
A. Fractions, Percents, and Percentages
Fractions are a way to represent a portion of a whole. When working with fractions, we often are required to convert them to decimals or express them as percentages. Percent means per hundred, and it is accompanied by a number and the % symbol (or the word percent).
Example 1. Explain the meaning of 15% (or 15 percent). 15% (or 15 percent) means 15 hundredths or 15100=0.15.
A percentage is a portion of a whole expressed in hundredths.
Example 2. Suppose 15 out of 20 students in a class are female. What percentage of the class is female?
The portion consists of 15 female students and the whole is the class of 20 students. Obtain the percentage as follows:
Divide the portion by the whole.
1520=0.75
Multiply by 100 and attach the % symbol.
(0.75×100)%=75%
The words percent and percentage are related to each other, but they do not have the same meaning. However, the use of percent for percentage is becoming more and more common, so don’t worry about the difference.
Some fraction-to-percent conversions require rounding, thereby changing the value slightly. Example 3 demonstrates how to round a percent.
Example 3. Express 313 as a percent and round to the nearest hundredth of a percent.
- First, convert the fraction to a decimal. A calculator with 10 places of accuracy will yield 0.2307692308.
- Second, multiply this number by 100 to obtain 23.07692308.
- Third, round to two decimal places (for the nearest hundredth of a percent) and then affix the percent symbol: 23.08%. (See Algebra Review II, item F, Rounding Numbers, page AR-5.)
Practice Exercises
- Explain the meaning of 25%.
- Suppose 10 out of 25 students in a class are male. What percentage of the class is male?
- In a survey of 500 students, 347 circled “Yes” in answer to a question. What percentage of those surveyed responded “Yes”?
- Express 618 as a percent and round to the nearest hundredth of a percent.
B. Remainders
To find the remainder when an integer a is divided by an integer b, we divide a by b using long division.
Example 1. Divide 95 by 7. What is the remainder?
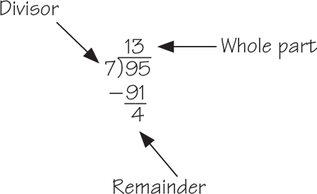
An important feature of a remainder is that it is always less than the divisor, and it can be 0.
Calculator Note: To use a calculator to find the remainder when a is divided by b, perform the following steps:
- STEP 1. Enter a÷b.
- STEP 2. Enter a−(whole part from Step 1)×b. The result will be the remainder.
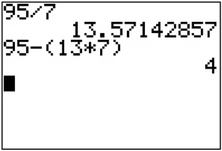
Example 2. Use a calculator to find the remainder when 95 is divided by 7.
- STEP 1. Enter 95÷7. The result is 13.57142857.
- STEP 2. Enter 95−(13×7). The result gives a remainder of 4. (See calculator screenshot.)
Practice Exercises
- Use long division to divide 108 by 8. What is the whole part? What is the remainder?
- Use long division to divide 227 by 6. What is the whole part? What is the remainder?
- Use long division to divide 141 by 3. What is the whole part? What is the remainder?
- A number divided by 5 results in a whole part of 6 and a remainder of 2. What is the number?
- A number divided by 9 results in a whole part of 14 and a remainder of 7. What is the number?
- Use a calculator to find the whole part and remainder when 76 is divided by 14.
- Use a calculator to find the whole part and the remainder when 141 is divided by 6.
- When two numbers are divided, can the remainder ever be larger than the whole part? Can the remainder ever be larger than the divisor?
C. Prime and Composite Numbers
An integer greater than 1 is prime if the only positive integers that divide it with a remainder equal to 0 are the number itself and 1. There are infinitely many prime numbers. The first ten are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29. A list of the first 1000 prime numbers can be found by searching Google for “1000 primes.”
A composite number is a positive integer that is greater than 1 and is not prime. One can use a list of primes and a calculator to determine whether any positive integer N is prime by dividing N, one by one, by all the primes less than or equal to √N. If one of the quotients is an integer, then N is not prime.
Example 1. Determine whether 147 is a prime or composite number.
Since √147≈12.12, we need only divide 147 by 2, 3, 5, 7, and 11. In this case, 147÷3=49, so 147 is not prime.
Example 2. Determine whether 151 is a prime or composite number.
Since √151≈12.28, we need only divide 151 by 2, 3, 5, 7, and 11. When 151 is divided by 2, 3, 5, 7, and 11, the quotient is never an integer, so 151 is prime.
The following are divisibility tests that can quickly identify that a positive integer is a composite number.
- Integers whose last digit is an even number are divisible by 2.
- Integers whose last digit is 0 or 5 are divisible by 5.
- Integers for which the sum of their digits is divisible by 3 are themselves divisible by 3.
Example 3. Determine whether 4785 and 2301 are prime or composite numbers.
Both are composite numbers. Using the divisibility tests:
- 4785 is divisible by 5, since its last digit is 5.
- 2301 is divisible by 3, since 2+3+0+1=6, which is divisible by 3.
Practice Exercises
Determine whether the following numbers are prime or composite numbers.
- 187
- 229
- 3342
- 899
- 1295
- 4221
- 421
- 3,476,210
D. significant Digits
All measurements introduce some degree of uncertainty due to the deficiencies of the measuring device or the person doing the measuring. It is this uncertainty that we take into consideration when dealing with significant digits. The rules for determining the number of significant digits are as follows:
- Any non-zero number is significant.
- Any 0 that lies both to the right of the decimal point and to the right of a non-zero digit is significant.
- Any 0 between significant digits is significant.
Example 1. Determine the number of significant digits for 10,134 and 2300.00.
The number 10,134 has five significant digits and 2300.00 has six significant digits.
Example 2. Determine the number of significant digits for 0. 200 and 0.000034.
Because the leading zero is not considered a significant digit, 0.200 has three significant digits, while 0.000034 has two.
In the context of significant digits, when multiplying (or dividing) numbers, we determine which of the original numbers has the smallest number of significant digits and round our product (or quotient) to match this smallest accuracy. (See Algebra Review II, item F, Rounding Numbers below.)
Example 3. Suppose that you had a box and measured to find a height of 4.8 inches, length of 5.4 inches, and width of 9.4 inches. Find the volume of the box.
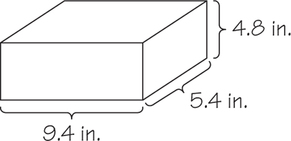
Each of these measurements has two significant digits. The volume of the box is found by multiplying length, width, and height. When this is done, we get a result of 243.648 cubic inches. However, because we had only two significant digits in our measurements, we must round this answer to 240 cubic inches.
When adding or subtracting, first perform the calculation with all the digits, and then round the sum or difference to have the same decimal places as the number with the least number of digits following the decimal point.
Example 4. Find the product and sum of the measurements 0. 012, 2.30, and 0.001, and then round appropriately.
The product of these numbers is 0.0000276. Because 0. 001 has only one significant digit, we round the answer to 0. 00003, which has one significant digit. The sum of the numbers is 2.313. Because 2.30 has the smallest accuracy in terms of decimal places, we round this sum to 2.31.
Some calculations involve numbers that are considered exact. Numbers such as exact conversion factors do not figure into determining the number of significant digits in a calculation.
Practice Exercises
For Practice Exercises 1–4, determine the number of significant digits.
- 1002
- 12,000
- 0.0035
- 0.0210
For Practice Exercises 5–8, use the box in the diagram that follows. Round your answers according to the conventions for significant figures and number of decimal places discussed above.
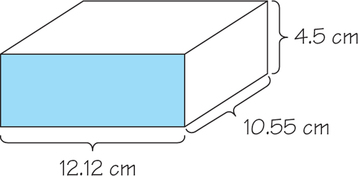
- Determine the volume of the box. Round appropriately.
- Determine the perimeter of the front face of the box shaded in blue.
- Determine the area of the front face of the box shaded in blue.
- Determine the area of the top of the box.
E. Scientific Notation
A number written in the form a×10n, where 1≤a<10 and n is an integer, is written in scientific notation. Scientific notation is a useful way to express very large or very small numbers.
Example 1. Write 568,000 in scientific notation.
568,000=5.68×105
Example 2. Write 0.0028 in scientific notation.
0.0028=2.8×10−3
(See Algebra Review VI, item B, Natural and Fractional Exponents, page AR-23.)
Most calculators and many computer programs use a shorthand version of scientific notation. Instead of indicating a multiplication by 10n, the calculator/computer program will write “E” followed by the power n. The base is understood to be 10.
Example 3. Write the numbers in Examples 1 and 2 as they might appear on a calculator.
568,000 might appear as 5.68 E5.0. 0028 might appear as 2.8 E−3.
Warning: This is entirely different from (5.65)5 or (2.8)−3.
Practice Exercises
- Write 495,000,000 in scientific notation.
- Write 0.00000072 in scientific notation.
- Write your answer to Practice Exercise 1 as it might appear on a calculator.
- Write your answer to Practice Exercise 2 as it might appear on a calculator.
- Use your calculator to find the value of 525. Write the answer both with and without using scientific notation.
- Use your calculator to divide 467 by 200,000,000. Write the answer without using scientific notation.
F. Rounding numbers
In various exercises, you will be asked to round numbers to a certain place, such as the nearest thousands place or to two decimal places.
Case 1: Rounding to whole number places, such as ones, tens, hundreds, thousands, and so forth.
To round a number to a particular place, look at the digit in that place—we’ll call this the target digit—and then look at the digit to its right.
- If the digit to the right of the target digit is a 0, 1, 2, 3, or 4, then leave the target digit as it is and replace any digits to its right with 0s. Do not include a decimal point or any 0s to the right of a decimal point.
- If the digit to the right of the target digit is a 5, 6, 7, 8, or 9, then add 1 to the target digit and replace any digits to its right with 0s. Do not include a decimal point or any 0s to the right of a decimal point.
Case 2: Rounding to decimal places, such as tenths, hundredths, thousandths, and so forth.
To round a number to a particular place, look at the digit in that place—the target digit—and then look at the digit to its right.
- If the digit to the right of the target digit is a 0, 1, 2, 3, or 4, then leave the target digit as it is and omit any digits to its right.
- If the digit to the right of the target digit is a 5, 6, 7, 8, or 9, then add 1 to the target digit and omit any digits to its right.
Example 1. Round 67,853 (a) to the nearest hundreds and (b) to the nearest tens.
- (a) Locate the target digit, the number in the hundreds place—in this case, 8. Look at the digit one place to its right, which is 5. Since this digit is 5, add one to the target digit (8+1=9) and replace the digits to its right with 0s. The rounded number is 67,900.
- (b) Locate the target digit, the number in the tens place—in this case, 5. Look at the digit one place to its right, which is 3. Since this digit is less than 5, leave the target digit as it is and replace the digit to its right with 0. The rounded number is 67,850.
Example 2. Round 4.64779 (a) to one decimal place (the nearest tenths place) and (b) to two decimal places (the nearest hundredths place).
- (a) Locate the target digit, the digit in the tenths place—in this case, 6. Look at the digit one place to its right, which is 4. Since this digit is less than 5, leave the target digit as it is and omit any digits to its right. The rounded number is 4.6.
- (b) Locate the target digit, the digit in the hundredths place—in this case, 4. Look at the digit one place to its right, which is 7. Since this digit is greater than 5, add 1 to the target digit (4+1=5) and omit any numbers to its right. The rounded number is 4.65.
Example 3. Round 7.4997 to two decimal places.
Locate the target digit, the digit in the hundredths place—in this case, 9. Look at the digit one place to its right, which is also 9. Since this digit is greater than 5, add 1 to the target digit (9+1=10). Notice that this increases the digit in the tenths place. Omit any digits to the right of the target digit. The rounded number is 7.50.
Practice Exercises
- Round 48,749 to the nearest thousands place.
- Round 48,749 to the nearest hundreds place.
- Round 2.267 to one decimal place.
- Round 2.263 to two decimal places.
- Round 5.1997 to two decimal places.
G. Counting in Binary
The numeration system that we use every day is a base- 10 system, which involves 10 digits, 0 through 9. In order to exceed 9, we add a place and write the number 10. A number such as 307 can be written in expanded form as 307=3×100+0×10+7×1. Using exponential notation, we could also write the following:
307=3×102+0×101+7×100
Example 1. Write 1027 in expanded form using exponential notation.
1027=1×103+0×102+2×101+7×100
Notice in the exponential form shown in Example 1 that the base is 10. Binary is a base-2 system and has only two digits, namely 0 and 1. If we were to convert a binary number to its base-10 (decimal) equivalent, we would use a base of 2 in the same way we used the base of 10 in Example 1.
Example 2. Convert the binary number 1011 (read as “one zero one one”) to its base-10 equivalent.
The binary number 1011 is equivalent to the base-10 number:
1×23+0×22+1×21+1×20=8+0+2+1=11
After the number 1, a binary number will have at least two places. Starting with 0, the string of binary numbers in order is
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111…
When writing these numbers, we do not put commas in, as we do with decimal numbers. For example, the binary number 11011 would not be written as 11,011. Also, when binary numbers are used and the context is not clear whether the number is binary or base-10, a subscript of 2 is often included. Thus, 112 represents 11 base 2 (which is 3 in base-10) while 11 is the usual number “eleven.”
Practice Exercises
For Practice Exercises 1—5, convert the base-2 number to its equivalent in base-10.
- 1111002
- 10110112
- 100011002
- 111112
- 10010012
- If you were counting in base-2, what number comes after 111112?
- What base-2 number is equivalent to the base-10 number 35?
- What base-2 number is equivalent to the base-10 number 65?