Algebra Review III: Working with Formulas
A. Using Formulas
A formula is a statement that claims that two expressions are equal. When dealing with formulas, it is important to know what each variable represents. Generally, formulas are casesensitive, which means that an uppercase X may represent a different variable than a lowercase x. If more than one variable from the same type of variables is needed, then subscripts are often used.
Here are three examples of formulas.
The formula for finding the mean, Unexpected text node: 'x ', of n numbers x1, x2, …, xn is
ˉx=x1+x2+⋯+xnn.
The slope of a line is determined by two points often expressed as (x1, y1) and (x2, y2). The formula that relates these two points to the slope of the line that passes through them, commonly denoted as m, is
m=y2−y1x2−x1
For a principal P invested at an annual rate of interest r, the total amount A accumulated in the account after t years is
A=P(1+rt)
In most formulas, the value of the variable on the left is found by substituting values for the variable(s) on the right.
The following three steps occur when evaluating a formula to determine the numerical value of one of the variables:
- Understand what the variables in the formula represent.
- Carefully substitute the values that are given into the formula.
- Apply order of operations to simplify the expression.
Next, we consider some examples involving finding the mean, slope, and total amount.
Example 1. Find the mean of the numbers 2, , and 5.
First, assign a meaning to the numbers.
Second, substitute the constants for the variables.
Third, simplify by applying order of operations.
Example 2. Calculate the slope of the line that passes through () and (2, 5).
First, assign a meaning to the numbers.
Second, substitute the constants for the variables.
Third, simplify by applying order of operations.
(Notice that subtracting a negative number gives the same result as adding its opposite: .)
Example 3. Suppose that you invest $1000 in an account that pays 4% interest on the initial amount invested. How much money is in your account after 5 years?
First, assign a meaning to the numbers: The principal is the amount invested, . The 4% interest rate must be converted to its decimal equivalent, . The principal is invested for 5 years, so . We want to find , the amount in the account.
Second, substitute the constants for the variables.
Third, simplify by applying order of operations.
The amount of money in the account after 5 years is .
Sometimes when working with formulas, the variable for which you want to solve is not isolated on the left-hand side of the equation. In that case, additional algebraic manipulation is required to solve for the unknown variable. The following two common algebraic manipulations will often do the trick:
- Multiply or divide both sides of the equation by the same nonzero number.
- Add or subtract the same number from both sides of the equation.
Example 4. Suppose you are told that the mean of four numbers is 10, and you know that the first three numbers are 8, 12, and 6. What is the value of the fourth number?
First, assign a meaning to the numbers.
Second, substitute the constants for the variables.
Page AR-8Third, simplify by applying order of operations.
Fourth, apply further algebraic manipulation to solve for the unknown variable.
We have found that the fourth number must be 14.
Example 5. The slope of a line through two points is %. The first point has coordinates (1, 1). The -coordinate of the second point is 3. What is the x-coordinate of the second point?
First, assign a meaning to the numbers.
Second, substitute the constants for the variables.
Third, simplify by applying order of operations.
Fourth, apply further algebraic manipulation to solve for the unknown variable.
Calculator note: When calculating the value of a fraction, such as when you find the slope of a line given two points on the line, you must separately enclose both the numerator and denominator in parentheses.
Example 6. Using a calculator, find the slope of a line that passes through the points (5, 9) and (17, 6).
The keystrokes for a TI-84 graphing calculator would be:
which yields .
This is how this calculation should appear on your calculator screen.

Practice Exercises
Use the formulas above and the three-step method to find the answers to Practice Exercises 1–3.
- Find the mean of the numbers .
- Calculate the slope of a line passing through .
- A principal of $5000 is invested in an account that pays an annual rate of 3%. How much money is in the account after four years?
- The mean of five numbers is 4.4. Four of the numbers are 4, 2, 3, and 6. What is the fifth number?
- The slope of a line through two points, (2, 3) and (, 7), is . Find .
- The slope of a line through two points, (1, 7) and (3, ), is . Find .
- A principal was invested in an account paying an annual interest rate of 5%. After 10 years, the total amount in the account was $3750. Find .
- The formula for finding the area of a rectangle is , where is the area, is the length, and is the width. If a rectangle’s length is 7 cm and its area is , what is its width?
B. solving for one Variable in Terms of Another
Sometimes when working with formulas, the variable of interest is not isolated on the left-hand side of the equation. In that case, additional algebraic manipulation is required to solve for the variable of interest in terms of the remaining variables. The following two common algebraic manipulations will often do the trick:
- Multiply or divide both sides of the equation by the same nonzero number.
- Add or subtract the same number from both sides of the equation.
For example, is the formula for finding the circumference of a circle, , given its diameter, . However, in the context of forestry, a forester would measure a tree’s circumference in order to calculate its diameter. So, the forester would prefer having a formula that gives in terms of . Dividing both sides of this formula by gives
Example 1. Solve for .
If the equation involves a single radical expression involving the variable of interest, a different approach is needed. In that case, first isolate the radical on one side of the equation. Raise both sides of the equation to the power required to remove the radical. Finally, use the algebraic manipulations in the two bullets above to solve for the variable of interest in terms of the other variables. [For information on radicals and powers, see Algebra Review VI, item A, Powers and Roots (page AR-22), and item D, Rules for Exponents and Roots (page AR-25).]
Example 2. Solve for .
You can use the same technique used in Example 2 if the variable of interest is raised to a power.
Example 3. Solve .
Practice Exercises
Use the simple interest formula (from Chapter 21, page 871), , for Practice Exercises 1 and 2.
- Solve the simple interest formula for .
- Solve the simple interest formula for .
Use the compound interest formula (from Chapter 21, page 875), , for Practice Exercises 3 and 4.
- Solve the compound interest formula for .
- Solve the compound interest formula for .
C. Formulas Related to Geometric shapes
In Chapters 18 and 20, you will encounter a variety of twodimensional and three-dimensional geometric shapes. Formulas for perimeter and area are useful when dealing with two-dimensional shapes. Formulas for surface area and volume are useful when dealing with three-dimensional shapes. This section focuses on a few of the most commonly used two- and three-dimensional geometric shapes.
Two-Dimensional Shapes

Note: Squares are special cases of rectangles, where .

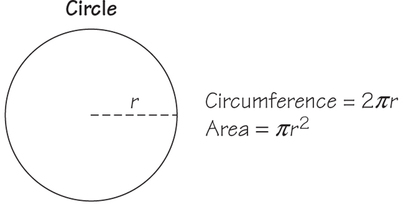
Note: For circles, the length around the circle is called the circumference rather than the perimeter.
Example 1. Jordon plans to fence in a 12-ft-by-8-ft rectangular enclosure for her dog. Determine the length of fencing needed to make the enclosure and the area that will be enclosed.
The perimeter gives the length of fencing that is needed: . The enclosed area is .
Three-Dimensional Shapes




Example 2. For a party, Cara made paper cones to hold candy and popcorn (see diagram).
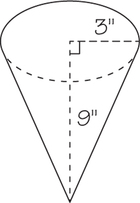
(a) After placing candy in some of the cones, Cara added a top to contain the candy. What is the surface area of each cone? Round your answer to two decimal places and include the units of measurement.
- (b) Cara filled the remaining open cones with popcorn. What is the surface area of one of the open cones?
For an open cone, we need to remove the area of the circular top. The area of a circle with a 3-in. radius is . The surface area is approximately , or
(c) What is the volume of one of Cara’s paper cones?
Practice Exercises
- A bicycle tire has a diameter of 26 in. How many inches does the bicycle travel each time the wheel makes one revolution?
- Suppose a square has an area of . What is the side length of the square?
A landscaper is creating a garden in the shape of a triangle (see diagram). He plans to put a metal edge around the garden plot. Find the length of metal edging needed.
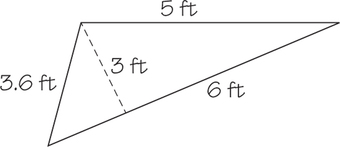
- In order to get the correct amount of mulch for the garden in Practice Exercise 3, the landscaper needs to know the area of the plot. What is the area?
- A cylindrical grain silo has a radius of 15 ft and height of 110 ft. What is the volume of grain that can be stored in the silo? What is the surface area of the silo?
- The diameter of a sphere is 12 in. What is the volume and surface area of the sphere?
- The height of a cone is 25 cm. The diameter of its circular base is 10 cm. Find the volume and surface area of the cone.