Algebra Review V: Summation Notation, Sequences, and Series
A. summation Notation
A sequence of numbers is an ordered list of numbers. If there are k numbers in a list, the sequence can be written as a1,a2,…,ak. A summation is the addition of the numbers in such a sequence. Summation notation has the following parts:
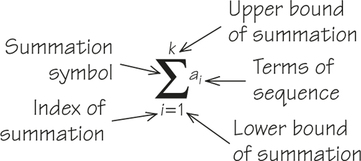
Example 1. Find the value of 3∑i=1i2.
The index i indicates that the summation starts at 1 and that successive values of i can be found by adding 1 until the upper bound of 3 is reached. Thus, we get
3∑i=1i2=12+22+32=14
Example 2. Find the value of 5∑i=13i.
We find 5∑i=13i as follows:
5∑i=13i=3(1)+3(2)+3(3)+3(4)+3(5)=3+6+9+12+15=45
If each term in a sum contains the same factor, we can use the distributive law to pull the factor out in front of the sum:
n∑i=1kai=kn∑i=1ai
Example 3. Return to Example 2. This time, pull the constant out in front of the summation.
5∑i=13i=35∑i=1i=3(1+2+3+4+5)=3(15)=45
We can also use summation notation to shorten formulas. In the next two examples, we revisit formulas for calculating the mean and standard deviation of a sample, this time using summation notation.
Example 4. In Chapter 5 (page 197), the formula for the mean of n numbers is given as ˉx=x1+x2+⋯xnn. Express this formula using summation notation.
We express the formula for ˉx using summation notation in the numerator: ˉx=∑ni=1xin..
Example 5. In Chapter 5 (page 204), the formula for the standard deviation of n data values is given as s=√(x1−ˉx)2+(x2−ˉx)2+⋯+(xn−ˉx)2n−1. Express this formula using summation notation.
We express the formula for s using summation notation in the numerator of the fraction:
s=√∑ni=1(xi−ˉx)2n−1
Up to this point, we have dealt with a single list of numbers. However, sometimes we combine corresponding elements of two ordered lists of numbers. When there are two lists of numbers, make sure to pair the values from both lists correctly.
Example 6. Determine 5∑i=1aibi. from the two lists of numbers in the following table.
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| a at ith position | 2 | −5 | 0 | 3 | −1 |
| b at ith position | 3 | 2 | −3 | 1 | 4 |
5∑i=1aibi=(2)(3)+(−5)(2)+(0)(−3)+(3)(1)+(−1)(4)=6+(−10)=6+(−10)+0+3+(−4)=−5
Practice Exercises
Find the value of the sums in Practice Exercises 1–3.
- 3∑i=1i3
- 5∑i=12i
- 4∑i=1(2i−1)
Suppose that x1=3,x2=5, and x3=4.
- (a) Use the formula in Example 4 to find ˉx.
- (b) Use your answer to part (a) and the formula in Example 5 to find s.
The table below contains two lists of numbers.
i 1 2 3 4 a at ith position 2 5 7 9 b at ith position 8 6 4 2 - (a) Determine 4∑i=1aibi.
- (b) Determine 4∑i=1(ai−bi).
B. sequences
A sequence is a listing of objects, generally numbers, called terms. Terms in a sequence are listed in a specific order and are separated by commas.
Example 1. Write a sequence of positive multiples of 3.
3,6,9,12…
The sequence in Example 1 goes on forever, and is therefore called an infinite sequence. Sequences that have a definite end are called finite.
Subscripts are used in sequences to describe where in the ordered list a term is located. For example, t1 could represent the first term of the sequence in Example 1. In this case, t1=3. (Sometimes the initial term in a sequence is represented by t0instead of t1.) Because the pattern in Example 1 continues, we know that t5=15.
Example 2. For the sequence in Example 1, given that t1 represents the first term, what is t8?
We can extend the sequence out to eight terms: 3,6,9,12,15,18,21,24,…. Thus, t8=24.
In general, tn represents the nth term, tn−1 is the term that precedes tn, and tn+1is the term that follows tn.
There are two types of rules that govern how terms in a sequence are calculated: explicit and recursive. An explicit rule defines how to find the nth term by direct calculation. A recursive rule defines the first or first few terms and then makes a general statement about how to obtain other terms from previous terms.
Example 3. Find an explicit rule for expressing the sequence of positive multiples of three. Use the explicit rule to determine t35.
We begin by examining the list below to look for an explicit pattern.
| Term Number | Term | Comment |
|---|---|---|
| 1 | 3 | t1=3⋅1 |
| 2 | 6 | t2=3⋅2 |
| 3 | 9 | t3=3⋅3 |
| 4 | 12 | t4=3⋅4 |
We can summarize the pattern in the last column of the table above with the explicit rule tn=3⋅n. Using this rule, we find t35=3⋅35=105.
Example 4. Find a recursive rule for describing the sequence of positive multiples of three. Use the recursive rule to determine t9 from Example 2′s answer.
We begin by examining the following list to look for a recursive pattern, a pattern that describes how to obtain the next term in a sequence from the previous term (or terms).
| Term Number | Term | Comment |
|---|---|---|
| 1 | 3 | t1=3 |
| 2 | 6 | t2=t1+3 |
| 3 | 9 | t3=t2+3 |
| 4 | 12 | t4=t3+3 |
A recursive rule about this sequence is t1=3 and tn=tn−1+3 for n≥2 (or tn+1=tn+3 for n≥1). To find t9, we need the value of the previous term, t8=24, which we get from Example 2. Next, we use the recursive rule to find t9:t9=t8+3=24+3=27.
Calculator Note: Calculators that store an answer for use with the next calculation can be used to easily generate a recursively defined sequence. Example 5 shows how to use this feature on a TI-84 graphing calculator. Example 6 shows how to use the ENTRY feature on a TI-84 to quickly generate terms of an explicitly defined sequence.
Example 5. Use a calculator to generate the first four terms of the following recursively defined sequence: t1=5 and tn=4⋅tn−1+1
Using a TI-84, here’s one way to generate terms in this sequence:
- Enter the value of the first term: press 5 ENTER.
- Press × 4+1 ENTER to obtain the second term in the sequence.
- Press ENTER to obtain the third term. Continue pressing ENTER to generate more terms.
Below is a calculator screen showing the first four terms of this sequence.

Example 6. Use a calculator to generate the first six terms of the following explicitly defined sequence: tn=n2−2.
Using a TI-84, here’s one way to generate terms in this sequence:
- Enter n=1 into the formula to get the first term, t1: press 1 x2 − 2 ENTER.
- To get the second term, press 2nd ENTER (for ENTRY), use the left arrow key to move the cursor over 1, and then press 2 (to replace 1 with 2) and ENTER.
- To get the third term, press 2nd ENTER, use the left arrow key to move the cursor over 2, and then press 3 (to replace 2 with 3) and ENTER.
- Repeat the process above to replace the value of n by 4, 5, and 6.
Below is a calculator screen that shows the first three terms of this sequence and entry of the fourth term prior to pressing ENTER. The first six terms of this sequence are −1,2,7,14,23, and 34.

Practice Exercises
- Write a sequence of positive multiples of 5.
- Write an explicit rule to generate positive multiples of 5. Use this rule to find the tenth term in the sequence.
- Write a recursive rule to generate positive multiples of 5.
For Practice Exercises 4–8, use the given rules to generate the first six terms in the sequence.
- an=12n
- b1=3 and bn=bn−1+2
- b1=3 and cn+1=3⋅cn−1
- dn=3n−2
- t1=1, t2=2, and tn=tn−1+tn−2
C. Arithmetic and Geometric sequences and series
An arithmetic sequence occurs when you add the same amount (common difference) to a term to obtain the next term. This relationship between term and term number is linear. A geometric sequence occurs when you multiply the same amount to a term (common ratio) to obtain the next term. This relationship between term and term number is exponential.
Suppose that each sequence has a first term a. For the arithmetic sequence, we add d to obtain the next term, and for the geometric sequence we multiply by r. We can find the nth term of each sequence by looking for a pattern.
| term number | Arithmetic | Geometric |
|---|---|---|
| 1 | a | a |
| 2 | a+d | ar |
| 3 | a+2d | ar2 |
| 4 | a+3d | ar3 |
| ⋮ | ⋮ | ⋮ |
| n | a+(n−1)d | arn−1 |
The nth term of an arithmetic sequence is a+(n−1)d, and the nth term of a geometric sequence is arn−1.
Example 1. Consider two specific sequences where the first term is 3. The first sequence, an arithmetic sequence, has a common difference of d=2. The second sequence, a geometric sequence, has a common ratio of r=2. Write the first eight terms of each sequence.
Arithmetic sequence: 3, 5, 7, 9, 11, 13, 15, 17
Geometric sequence: 3, 6, 12, 24, 48, 96, 192, 384
A series is made from a sequence of terms that are summed.
Example 2. Find the arithmetic series formed from the eight terms of the arithmetic sequence in Example 1.
The series is the sum of the terms in the sequence. You could find the sum by adding up all eight terms: 3+5+7+9+11+13+15+17. However, we would prefer to find the sum using a method that can be generalized when more terms are included. Notice the following pattern: The sum of the first and last term is 20 and that sum appears three more times.
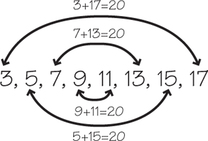
The series (the sum of the eight terms in the sequence) is 4⋅20=80.
In general, we can extend the pattern noted in Example 2 to find the sum of the first n terms of an arithmetic sequence. Here’s the result:
(number of terms, n2) × (first term + last term)
We can express the series formed from the first n terms in an arithmetic sequence a1,a2,a3, using summation notation:
Sn=n∑i=1ai=n(a1+an)2
Example 3. Given an arithmetic sequence with terms specified by an=3+2(n−1), find the value of the series S10, which is the sum of the first 10 terms of the sequence.
Start by determining the first and tenth term in the sequence: a1=3+2(1−1)=3 and a10=3+2(10−1)=21. Next, use the formula above for finding the sum of terms in an arithmetic sequence: S10=10(3+21)2=2402=120.
A geometric series is made by summing the terms of a geometric sequence. The sum of terms in a geometric sequence can be computed from the geometric series rule, which is
Sn=a(rn−1r−1)
where a is the first term and r is the common ratio.
Example 4. Find the geometric series formed from the sum of the eight terms in the geometric sequence in Example 1.
Substituting 3 for a, 2 for r, and 8 for n into the geometric series rule, we have
S8=3(28−12−1)=3(256−11)=3(255)=765
Practice Exercises
For Practice Exercises 1–4, determine whether the sequence is arithmetic, geometric, or neither, and then write the next two terms in the sequence.
- 5, 10, 20, 40, 80
- 2,−2,4,−4,6,−6
- 4, 7, 10, 13, 16
- 200, 100, 50, 25
- An arithmetic sequence has first term −12 and common difference d=5. What are the first five terms of this sequence? What is the sum of the first five terms, S5?
- A geometric sequence has first term 5 and common ratio r=4. What are the first five terms of this sequence? What is the sum of the first five terms, S15?
- Given an arithmetic sequence with terms specified by an=1+4(n−1), find S5.
- Given a geometric sequence with first term a=2 and common ratio r=3, find S15