APPENDIX | Algebra Review

Algebra Review VI: Exponents, Roots, and Logarithms

A. Powers and Roots

Powers

A positive integer exponent or power is a convenient shorthand for indicating repeated multiplication of a number $a$ called the base. For example, the expression $a^{2}$ , read as “ $a$ squared,” means $a$ multiplied by $a$ . When either a positive or negative number is squared, the outcome will always be positive. When 0 is squared, the outcome is 0.

Example 1. Simplify ${(- 8)}^{2}$ .

${(- 8)}^{2} = (- 8) (- 8) = 64$

The expression $a^{3}$ is read as “ $a$ cubed” and $a^{n}$ is read as “ $a$ to the $n$ th power,” or simply “ $a$ to the $n$ .” For positive integer powers of $n$ , it means that $a$ is multiplied times itself $n$ times.

$a^{n} = \underset{n times}{\underset{︸}{a \cdot a \cdot a \dots a}}$

Example 2. Simplify $2^{5}, {(- 2)}^{3}$ , and ${(- 3)}^{4}$ .

$\begin{matrix} 2^{5} = (2) (2) (2) (2) (2) = 32 \\ (- 2)^{3} = (- 2) (- 2) (- 2) = - 8 \\ (- 3)^{4} = (- 3) (- 3) (- 3) (- 3) = 81 \end{matrix}$

Notice that when a negative number is raised to an odd power, the result is negative, but when a negative number is raised to an even power, the result is positive.

Calculator Note: When raising negative numbers to powers, always be sure to enclose the negative number in parentheses before hitting the power key.

Example 3. Use a calculator to determine the square of $- 4$ .

On a TI-84, use the keystrokes $\begin{matrix} ( \end{matrix} \begin{matrix} (-) \end{matrix} \begin{matrix} 4 \end{matrix} \begin{matrix} ) \end{matrix} \begin{matrix} ^ \end{matrix} \begin{matrix} 2 \end{matrix}$ $\begin{matrix} ENTER \end{matrix}$ . (Other calculators should be similar.) The result is ${(- 4)}^{2} = 16$ (see the calculator screenshot below on the left).

Example 4. Repeat Example 3, but don’t enclose $- 4$ in parentheses.

On a TI-84, use the keystrokes $\begin{matrix} (-) \end{matrix} \begin{matrix} 4 \end{matrix} \begin{matrix} ^ \end{matrix} \begin{matrix} 2 \end{matrix} \begin{matrix} ENTER \end{matrix}$ , which gives the result $- 4^{2} = - 16$ (see the calculator screenshot above on the right). In this case (based on order of operations), 4 was squared first, resulting in 16, and then its opposite was taken, resulting in a final answer of $- 16$ .

Roots

The expression $\sqrt{a}$ indicates a number that we square to get $a$ . The expression $\sqrt{a}$ is called the “principal square root of $a$ ,” and the outcome is never negative. The expression Va, read as the “ $\sqrt[n]{a}$ $n$ th root of $a$ ,” is the number that we raise to the $n$ th power to get $a$ .

$\sqrt[n]{a} = b means b^{n} = a$

Example 5. Determine $\sqrt{144}$ and $\sqrt[5]{32}$ .

$\sqrt{144} = 12 because 12^{2} = 144$

$\sqrt[5]{32} = 2 because 2^{5} = 32$

When a square root (or an $n$ th root) involves operations, it may be easier to simplify some of the calculations before taking the square root (or the $n$ th root).

Example 6. Approximate $\sqrt{\frac{(3.1) (2.7)}{5}}$ to one decimal place.

$\sqrt{\frac{(3.1) (2.7)}{5}} = \sqrt{\frac{8.37}{5}} = \sqrt{1.674} \approx 1.3$

Example 7. The standard deviation of a set of numbers (introduced in Chapter 5 on page 204) involves a square root. Find the standard deviation of 2, $- 3$ , and 5. Give a simplified exact answer and an approximation to two decimal places.

The formula for computing the standard deviation of a set of numbers is

$s = \sqrt{\frac{{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + \dots + {(x_{n} - \bar{x})}^{2}}{n - 1}}$

We follow the three steps from Algebra Review III, item A, Using Formulas (page AR-7).

First, assign a meaning to the numbers.

$n = 3$ and, $x_{1} = 2$ , $x_{2} = - 3$ , and $x_{3} = 5$ . From Example 1 in item A, Using Formulas, we calculated the mean of 2, $- 3$ , and 5 and found that $\bar{x} = \frac{4}{3}$ .

Page AR-23
Second, substitute the constants for the variables.

$\begin{matrix} s = \sqrt{\frac{{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + {(x_{3} - \bar{x})}^{2}}{n - 1}} \\ = \sqrt{\frac{{(2 - \frac{4}{3})}^{2} + {(- 3 - \frac{4}{3})}^{2} + {(5 - \frac{4}{3})}^{2}}{3 - 1}} \end{matrix}$
Third, simplify by applying order of operations.

$\begin{matrix} s = \sqrt{\frac{{(2 - \frac{4}{3})}^{2} + {(- 3 - \frac{4}{3})}^{2} + {(5 - \frac{4}{3})}^{2}}{3 - 1}} \\ = \sqrt{\frac{{(\frac{2}{3})}^{2} + {(- \frac{13}{3})}^{2} + {(\frac{11}{3})}^{2}}{2} = \sqrt{\frac{\frac{4}{9} + \frac{169}{9} + \frac{121}{9}}{2}}} \\ = \sqrt{\frac{\frac{294}{9}}{2} =} \sqrt{\frac{294}{18}} = \sqrt{\frac{49}{3}} = \frac{1}{\sqrt{3}} \approx 4.04 \end{matrix}$

Calculator Note: You can find a decimal approximation for the problem in Example 7 by entering the entire expression into your calculator before pressing the $\begin{matrix} ENTER \end{matrix}$ . The keystrokes for using a TI-84 to calculate the standard deviation of 2, $- 3$ , and 5 are given below.

Press $\begin{matrix} 2 nd \end{matrix} \begin{matrix} x^{2} \end{matrix} (for \sqrt ()$
$\begin{matrix} ( \end{matrix} \begin{matrix} ( \end{matrix} \begin{matrix} 2 \end{matrix} \begin{matrix} - \end{matrix} \begin{matrix} 4 \end{matrix} \begin{matrix} \div \end{matrix} \begin{matrix} 3 \end{matrix} \begin{matrix} ) \end{matrix} \begin{matrix} \circ \end{matrix} \begin{matrix} 2 \end{matrix} \begin{matrix} + \end{matrix}$
$\begin{matrix} ( \end{matrix} \begin{matrix} (-) \end{matrix} \begin{matrix} 3 \end{matrix} \begin{matrix} - \end{matrix} \begin{matrix} 4 \end{matrix} \begin{matrix} \div \end{matrix} \begin{matrix} 3 \end{matrix} \begin{matrix} ) \end{matrix} \begin{matrix} \circ \end{matrix} \begin{matrix} 2 \end{matrix} \begin{matrix} + \end{matrix}$
$\begin{matrix} ( \end{matrix} \begin{matrix} 5 \end{matrix} \begin{matrix} - \end{matrix} \begin{matrix} 4 \end{matrix} \begin{matrix} \div \end{matrix} \begin{matrix} 3 \end{matrix} \begin{matrix} ) \end{matrix} \begin{matrix} \circ \end{matrix} \begin{matrix} 2 \end{matrix} \begin{matrix} ) \end{matrix} \begin{matrix} \div \end{matrix} \begin{matrix} ( \end{matrix} \begin{matrix} 3 \end{matrix} \begin{matrix} - \end{matrix} \begin{matrix} 1 \end{matrix} \begin{matrix} ) \end{matrix} \begin{matrix} ) \end{matrix}$
Finally, press $\begin{matrix} ENTER \end{matrix}$ .

After entering these keystrokes, your calculator screen should match the one below.

Warning: When entering expressions involving parentheses into a calculator, make sure every left parenthesis has a matching right parenthesis. Also, notice that some commands, such as the square root command, may automatically include a left parenthesis that you will need to pair with a right parenthesis.

Calculator Note: The TI-84 has a square root key but no $n$ th root key. Here’s how to compute the nth root of a number $a$ , $\sqrt[n]{a}$ , when $n \geq 3$ :

Enter the value for $n$ .
Press $\begin{matrix} MATH \end{matrix} \begin{matrix} 5 \end{matrix} (for \sqrt[x]{})$ .
Enter the number $a$ and press $\begin{matrix} ENTER \end{matrix}$ .

Practice Exercises

Evaluate the following by hand. (Feel free to check your results using a calculator.)
- (a) ${(- 3)}^{4}$
- (b) ${(- 2)}^{5}$
- (c) $4^{3}$
Evaluate the following by hand. (Feel free to check your results using a calculator.)
- (a) $\sqrt[4]{10, 000}$
- (b) $\sqrt[3]{0.008}$
- (c) $\sqrt{2500}$
Approximate $\sqrt{\frac{{(2.7)}^{2} + 3 (4.6)}{4}}$ to one decimal place.
The dataset 1, 3, 5, 7 has mean $\bar{x} = 4$ . Determine the standard deviation (round your answer to two decimal places).
Use your calculator to approximate ${(1 + 0.05)}^{6}$ to two decimal places.

B. natural and Fractional Exponents

We can extend the definition of exponent to 0 and negative integers as follows:

$\begin{matrix} a^{0} = 1, a \neq 0 \\ a^{- n} = \frac{1}{a^{n}}, a \neq 0 \end{matrix}$

Example 1. Determine the values of $3^{0}, 2^{- 4}$ , and $- 3^{- 2}$ .

$\begin{array}{l} 3^{0} = 1 \\ 2^{- 4} = \frac{1}{2^{4}} = \frac{1}{16} \\ - 3^{- 2} = - (\frac{1}{3^{2}}) & \begin{array}{l} Order of operations tells us that powers \\ are performed before multiplication . \end{array} \\ = - \frac{1}{9} & \begin{array}{l} Taking the opposite of a number is \\ equivalent to multiplication by - 1 . \end{array} \end{array}$

Next, we extend the definition of exponent to fractions, in other words, exponents in the form $\frac{m}{n}$ with $m$ and $n$ integers and $n > 0$ .

$\begin{array}{l} a^{\frac{1}{n}} = \sqrt[n]{a}, a \geq 0 if n is even \\ a^{\frac{m}{n}} = \sqrt[n]{a^{m}} = {(\sqrt[n]{a})}^{m} \end{array}$

In defining $\frac{m}{a^{n}}$ (with $a \geq 0$ if $n$ is even), it doesn’t matter if you raise $a$ to the mth power first or take the $n$ th root of $a$ first. You can do whichever is easier.

Example 2. Determine $36^{\frac{1}{2}}$ and $8^{\frac{2}{3}}$ .

$36^{\frac{1}{2}} = \sqrt{36} = 6$

$8^{\frac{2}{3}} = {(\sqrt[3]{8})}^{2} = {(2)}^{2} = 4$

$8^{\frac{2}{3}} = \sqrt[3]{8^{2}} = \sqrt[3]{64} = 4$

In the computation of 8³, notice that it does not matter whether we took the cube root of 8 first and then squared the result or squared 8 first and then took the cube root.

Page AR-24

Example 3. Write the following radical expressions using exponents: $\sqrt[5]{x}$ and ${(\sqrt[3]{x})}^{2}$ .

$\begin{matrix} \sqrt[5]{x} = \frac{1}{x^{5}} \\ ({\sqrt[3]{x}}^{2}) = x^{\frac{2}{3}} \end{matrix}$

Calculator Note: When using a calculator, it may be easier to compute a constant raised to an exponent rather than the equivalent radical expression. See Example 4.

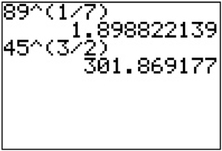
Example 4. Convert the following radical expressions to expressions involving exponents, and then use your calculator to approximate the values to two decimal places: $\sqrt[7]{89}$ and ${(\sqrt{45})}^{3}$ .

$\begin{matrix} \sqrt[7]{89} = 89^{\frac{1}{7}} \approx 1.90 \\ {(\sqrt{45})}^{3} = 45 \frac{3}{2} \approx 301.87 \end{matrix}$

Here’s how these computations should appear on a TI-84 graphing calculator. Notice that the fractional exponents are enclosed in parentheses.

Evaluate the following by hand.
- (a) $42^{0}$
- (b) $5^{- 2}$
Evaluate the following by hand.
- (a) ${(- 27)}^{\frac{1}{3}}$
- (b) ${(- 27)}^{\frac{2}{3}}$
Write the following radical expressions using exponents.
- (a) $\sqrt[10]{x}$
- (b) $\sqrt[5]{x^{3}}$
Convert the following radical expressions to expressions involving exponents, and then use your calculator to approximate the values to two decimal places.
- (a) $\sqrt{0.0026}$
- (b) ${(\sqrt[5]{256})}^{2}$
- (c) $\frac{1}{\sqrt{40}}$

C. Graphs of Exponential Equations

Equations of the form $y = c \cdot a^{x}$ are called exponential equations (or exponential functions). In such equations, the independent variable, $x$ , is an exponent. To understand the behavior of such a relation, we can sketch a graph by plotting points and then drawing a smooth curve through the plotted points.

Example 1. Determine points on the graph of $y = 10^{x}$ , plot these points, and then draw a graph $y = 10^{x}$ . Compare the graph of this exponential function with the graph of $y = x$ .

We begin by determining points on the graph of $y = 10^{x}$ .

$x$	$y = 10^{x}$
2	$10^{2} = 100$
1	$10^{1} = 10$
1/2	$10^{\frac{1}{2}} = \sqrt{10} \approx 3.16$
0	$10^{0} = 1$
$- 1 / 2$	$10^{- \frac{1}{2}} = \frac{1}{\sqrt{10}} \approx 0.32$
$- 1$	$10^{- 1} = \frac{1}{10} = 0.1$
$- 2$	$10^{- 2} = \frac{1}{10^{2}} = \frac{1}{100} = 0.01$

After plotting these points, we draw a smooth curve through them to obtain a graph of $y = 10^{x}$ . Then we add a graph $y = x$ . The graphs of these two equations appear below.

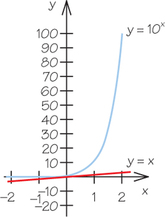
By comparing the graphs of $y = 10^{x}$ and $y = x$ , we can see that as the values of $x$ increase, the $y$ -values of the exponential equation increase faster than those of the linear equation. This will be true for exponential equations of the form $y = a^{x}$ , where $a > 1$ .

Practice Exercises

Without the aid of a calculator, complete the table below to get coordinates of some points on the graph of $y = 4^{x}$ .

$x$	$- 2.0$	$- 1.5$	$- 1.0$	$- 0.5$	0.0	0.5	1.0	1.5	2.0
$y = 4^{x}$

Page AR-25

Sketch by hand the graph of $y = 4^{x}$ . (Use an x-interval from $- 2$ to 2.)
Graph $y = e^{x}$ and $y = 2^{x}$ on the same set of axes. Use an $x$ -interval from 0 to 2. You will need a graphing calculator. [ $e \approx 2.718$ and is called the natural base. On a TI-84 graphing calculator, press $\begin{matrix} 2nd \end{matrix} \begin{matrix} LN \end{matrix} (for e^{x})$ .]

D. Rules for Exponents and Roots

Rules for Exponents

When multiplying two exponential expressions with the same base, the rule is to add the exponents.

$a^{m} a^{n} = a^{m + n}$

The statement above is easily understood when expanding the multiplication in a problem such as the following:

$2^{3} \cdot 2^{4} = \underset{7 times}{\underset{︸}{\underset{3 times}{\underset{︸}{2 \cdot 2 \cdot 2}} \cdot \underset{4 times}{\underset{︸}{2 \cdot 2 \cdot 2 \cdot 2}}}} = 2^{3 + 4} = 2^{7}$

Example 1. Simplify $3^{5} \cdot 3^{4}$ and $7^{\frac{4}{3}} \cdot 7^{\frac{1}{3}}$ .

$\begin{matrix} 3^{5} \cdot 3^{4} = 3^{5 + 4} = 3^{9} \\ 7^{\frac{4}{3}} \cdot 7^{\frac{1}{3}} = 7^{\frac{4}{3} + \frac{1}{3}} = 7^{\frac{5}{3}} \end{matrix}$

When dividing two exponential expressions with the same base, subtract the exponents.

$\frac{a^{m}}{a^{n}} = a^{m - n}, a \neq 0$

This last statement is easily understood when simplifying a problem, such as $\frac{2^{5}}{2^{3}}$ , by cancelling as follows:

Using cancellation: $\frac{2^{5}}{2^{3}} = \frac{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2}{2 \cdot 2 \cdot 2} = 2^{2}$
Using the rule for quotients: $\frac{2^{5}}{2^{3}} = 2^{5 - 3} = 2^{2}$

Example 2. Determine the value of $\frac{4^{3}}{4^{3}}$ and $\frac{4^{3}}{4^{6}}$ by cancellation and by using the rule for quotients.

$\begin{array}{l} \frac{4^{3}}{4^{3}} = \frac{4 \cdot 4 \cdot 4}{4 \cdot 4 \cdot 4} = 1 and \frac{4^{3}}{4^{3}} = 4^{3 - 3} = 4^{0} = 1 \\ \frac{4^{3}}{4^{6}} = \frac{4 \cdot 4 \cdot 4}{4 \cdot 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4} = \frac{1}{4^{3}} and \frac{4^{3}}{4^{6}} = 4^{3 - 6} = 4^{- 3} = \frac{1}{4^{3}} \end{array}$

When raising an exponential expression to a power, multiply powers.

${(a^{m})}^{n} = a^{m \times n}$

To see how this rule works, we expand ${(2^{3})}^{2}$ .

${(2^{3})}^{2} = \underset{2 \times 3 = 6 times}{\underset{︸}{\underset{2 times}{\underset{︸}{2^{3} \cdot 2^{3}}} = \underset{3 times}{\underset{︸}{2 \cdot 2 \cdot 2}} \cdot \underset{3 times}{\underset{︸}{2 \cdot 2 \cdot 2}}}} = 2^{2 \times 3} = 2^{6}$

Example 3. Simplify ${(4^{5})}^{3}$ both by expanding and by using the rule for raising to powers.

Using expansion:

$\begin{matrix} {(4^{5})}^{3} = \underset{3 times}{\underset{︸}{4^{5} \times 4^{5} \times 4^{5}}} \\ = \underset{3 \times 5 = 15 times}{\underset{︸}{\underset{5 times}{\underset{︸}{4 \cdot 4 \cdot 4 \cdot 4 \cdot 4}} \times \underset{5 times}{\underset{︸}{4 \cdot 4 \cdot 4 \cdot 4 \cdot 4}} \times \underset{5 times}{\underset{︸}{4 \cdot 4 \cdot 4 \cdot 4 \cdot 4}}}} = 4^{15} \end{matrix}$
Using the rule for raising to powers: ${(4^{5})}^{3} = 4^{5 \times 3} = 4^{15}$

Warning: Don’t touch this! There is no “distributive law for exponents.” That is, in general,

${(a + b)}^{n} \neq a^{n} + b^{n}$

Example 4. A student wrote the following equation on a test: ${(x + 2)}^{2} = x^{2} + 4$ . What is wrong with the student’s work? Correct the error.

The student tried to distribute the square power over the addition in $x + 2$ . However, there is no distributive law for exponents. Instead the student should use the distributive law to expand the square.

$\begin{array}{l} {(x + 2)}^{2} = (x + 2) (x + 2) & Expand the square . \\ = (x + 2) (x) + (x + 2) (2) & Use the distributive law . \\ = (x) (x) + (2) (x) + (x) (2) + (2) (2) & \begin{array}{l} Use the distributive law \\ a second time . \end{array} \\ = x^{2} + 4 x + 4 & \begin{array}{l} Combine like terms and \\ simplify . \end{array} \end{array}$

Rules for Roots

$\sqrt[n]{a b} = \sqrt[n]{a} \cdot \sqrt[n]{b}$

$\sqrt[n]{\frac{a}{b} =} \frac{\sqrt[n]{a}}{\sqrt[n]{b}}$

The rules for roots may help us calculate a root by hand, as shown in Example 5.

Example 5. Evaluate $\sqrt{490, 000}$ and $\sqrt{0.0036}$ by hand.

$\sqrt{490, 000} = \sqrt{49 \cdot 100 \cdot 100} = \sqrt{49} \cdot \sqrt{100} \cdot \sqrt{100} = 7 \cdot 10 \cdot 10 = 700$

$\sqrt{0.0036} = \frac{\sqrt{36}}{\sqrt{10, 000}} = \frac{\sqrt{6 \cdot 6}}{\sqrt{100 \cdot 100}} = \frac{\sqrt{6^{2}}}{\sqrt{100} \cdot \sqrt{100}} = \frac{6}{10 \cdot 10} = 0.06$

The rules of roots can sometimes be used to simplify an expression containing a radical, as shown in Example 6.

Example 6. Simplify $\sqrt{9 x^{3}}$ .

$\sqrt{9 x^{3}} = \sqrt{9 x^{2} \cdot x} = \sqrt{9 x^{2}} \cdot \sqrt{x} = 3 x \sqrt{x}$

Warning: Don’t touch this! There is no rule that is the “distributive law for radicals.” That is, in general,

$\sqrt[n]{a + b} \neq \sqrt[n]{a} + \sqrt[n]{b}$

Example 7. A student wrote the following on a test: $\sqrt{16 + 9} = \sqrt{16} + \sqrt{9} = 7$ . What is wrong with the student’s work? Show the correct calculations.

There is no rule for addition of radicals. Instead, simplify the number under che radical sign first and then take the square root: $\sqrt{16 + 9} = \sqrt{25} = 5$ .

Practice Exercises

In Practice Exercises 1–10, use the rules of exponents to simplify.

Page AR-26

$4^{3} \cdot 4^{7}$
$\frac{10^{8}}{10^{4}}$
${(4^{2})}^{5}$
$6^{\frac{3}{2}} \cdot 6^{- \frac{1}{2}}$
$3^{5} \cdot 3$
${(5^{3})}^{- 2}$
$\frac{7^{\frac{5}{2}}}{7^{\frac{1}{2}}}$
${(\frac{1}{6^{2}})}^{4}$
$\frac{3^{3}}{3^{10}}$
$5^{\frac{1}{6}} \cdot 5^{\frac{1}{3}}$

In Practice Exercises 11 and 12, use the rules of roots (as shown in Example 5) to evaluate the root by hand.

$\sqrt{6400}$
$\sqrt{0.0049}$
A student wrote the following on a test: $\sqrt{64 + 4} = \sqrt{64} + \sqrt{4} = 8 + 2$ . What is wrong with the student’s work? Use your calculator to approximate the correct answer to two decimal places.

E. Logarithms

A logarithm is an exponent, which represents the power that a number must be raised to in order to get another number: ${log}_{b} x$ is the power that $b$ must be raised to in order to get $x$ . We read the expression ${log}_{b} x$ as “the base- $b$ logarithm of $x$ .”

Example 1. Determine ${log}_{3} 9$ and ${log}_{3} 81$ .

${log}_{3} 9 = 2$ because 3 must be raised to the second power in order to get 9.

${log}_{3} 81 = 4$ because 3 must be raised to the fourth power in order to get 81.

Notice that a logarithmic equation has a corresponding exponential equation:

${log}_{3} 9 = 2$ because $3^{2} = 9$

${log}_{3} 81 = 4$ because $3^{4} = 81$

The subscript (or base) of the logarithmic equation is also the base of the corresponding exponential equation.

Because our number system is base 10, we often use a base-10 logarithm, which is also called a common logarithm. For common logarithms, the base is often omitted. On most calculators the $\begin{matrix} LOG \end{matrix}$ key computes the base-10 logarithm of a number.

$log x = {log}_{10} x$

Example 2. Determine log(1000), log(10), and log(1).

$log (1000) = {log}_{10} 1000 =$ the power to which 10 must be raised in order to get 1000. Since $10^{3} = 1000$ , we find that $log (1000) = 3$ .
$log (10) = {log}_{10} 10 = 1 because 10^{1} = 10$
$log (1) = {log}_{10} 1 = 0 because 10^{0} = 1$

The following two properties are true for logarithms when $x > 0$ :

$a^{{log}_{a} x} = x$ , and for base 10, $10^{log x} = x$
${log}_{a} x^{r} = r {log}_{a} x$ , and for base 10, $log x^{r} = r log x$

Example 3. Simplify $10^{2 + 3 log x}$ for $x > 0$ .

$\begin{array}{l} 10^{2 + 3 log x} & Apply logarithm property 2 . \\ 10^{2 + 3 log x} = 10^{2 + log x^{3}} & \begin{array}{l} Use the rule of exponents : \\ a^{m + n} = a^{m} a^{n} \end{array} \\ \begin{matrix} = 10^{2} 10^{log x^{3}} \\ = 100 x^{3} \end{matrix} & Apply logarithm property 1 . \end{array}$

Another important base is $e$ , which is used in continuously compounding interest problems. Like the more familiar number $π$ , $e$ is an irrational number—that is, a nonrepeating, nonterminating decimal. Its value is approximately 2.718. The base-e logarithm could be written as ${log}_{e} x$ . Mathematics, however, uses a special notation for base- $e$ logarithms, ln $x$ , and a special title, the natural logarithm.

Practice Exercises

For Practice Exercises 1–8, determine the value of the logarithm.

${log}_{2} 16$
${log}_{5} 1$
${log}_{5} 25$
log(10,000)
$log (\frac{1}{10})$
$log (\frac{1}{100})$
ln(1)
ln( $e$ )

Simplify the expressions in Practice Exercises 9 and 10.

$10^{3 + 2 log x}$
$10^{1 - 4 log x}$

F. Using Logarithms to solve Equations

When an equation contains the variable of interest as an exponent, using logarithms can help solve the equation. In this section, we use the natural logarithm, the logarithm with a base of $e$ , ln $x = {log}_{e} x$ . (Another approach would be to use the common logarithm, $log x = {log}_{10} x$ .)

Page AR-27

Example 1. Solve $2 x = 10$ .

Because $2^{3} = 8 and 24 - 16$ , we can estimate that the value of $x$ is between 3 and 4. Although we know the value of $x$ is closer to 3, we can’t state its exact value without logarithms. By taking the natural logarithm of both sides of the equation, we can get an exact solution. Here are the steps:

$\begin{array}{l} 2^{x} = 10 & \begin{array}{l} Take the natural logarithm of \\ both sides of the equation . \end{array} \\ ln (2 x) = ln (10) & \begin{array}{l} Use logarithm property 2 \\ [see Algebra Review VI, item E, \\ Logarithms (page AR - 26)] to move \\ the x in front of the logarithm . \end{array} \\ x ln (2) = ln (10) & Divide both sides of the equation by ln (2) . \\ x = \frac{ln (10)}{ln (2)} \end{array}$

Using a calculator and rounding to two decimal places, we find that the approximate power is $x = 3.32$ .

In the equation $A = P {(1 + i)}^{n}$ , when the variables $P$ , $i$ , and $n$ are stated, $A$ can be found by direct calculation. Solving for $P$ or $i$ is also straightforward (see Practice Exercises 3 and 4 in Algebra Review III, item B, Solving for One Variable in Terms of Another, page AR-9). However, if we want to solve $A = P {(1 + i)}^{n}$ for the exponent $n$ , we again turn to the technique of taking the natural logarithm of both sides of the equation.

Example 2. Solve $A = P {(1 + i)}^{n}$ for $n$ .

$\begin{array}{l} P {(1 + i)}^{n} = A & \begin{array}{l} We switched the right and lef t \\ sides of the equation . Isolate the \\ expression with n by dividing \\ both sides of the equation by P . \end{array} \\ {(1 + i)}^{n} = \frac{A}{P} & \begin{array}{l} Take the natural logarithm of both \\ sides . \end{array} \\ ln {(1 + i)}^{n} = ln (\frac{A}{p}) & \begin{array}{l} Use logarithm property 2 to move \\ the exponent in front of the logarithm . \end{array} \\ n ln (1 + i) = ln (\frac{A}{p}) & Divide both sides by ln (1 + i) . \\ n = \frac{ln (\frac{A}{p})}{ln (1 + i)} \end{array}$

Practice Exercises

In Practice Exercises 1–3, find an exact solution, and then use your calculator to determine an approximate solution to two decimal places.

$3^{x} = 15$
$2 \cdot 5^{x} = 28$
$80 {(1.03)}^{t} = 100$
Given $A = P {(1 + i)}^{n}$ , where $A = 2000, P = 1000, and i = 0.04$ , find the exact value for $n$ . Then find an approximation to two decimal places.