APPENDIX | Algebra Review

Algebra Review VIII: Permutations and Combinations

A. Permutations

A permutation is an arrangement or order of distinct elements in a set. The number of permutations or arrangements of $n$ distinct objects is $n$ ! (pronounced “ $n$ factorial”).

$n! = (n) (n - 1) (n - 2) \dots (2) (1)$

Example 1. How many ways can you arrange five books on a shelf?

There are 5! possible ways to arrange five books on a shelf.

$5! = (5) (4) (3) (2) (1) = 120$

Example 2. Use the answer in Example 1 to help determine the number of ways to arrange seven books on a shelf.

There are 7! possible ways to arrange seven books on a shelf.

$7! + 7 \cdot 6 \cdot \overset{5!}{\overset{︷}{5 \cdot 4 \cdot 3 \cdot 1}} = 7 \cdot 6 \cdot 5! = 7 \cdot 6 \cdot 120 = 5040$

Suppose that instead of choosing all five of the books and arranging them as in Example 1, you only had space on your shelf for three books. In this case, you want “the number of permutations of five books taken three at a time,” which we express as $_{5} P_{3}$ . More generally, the number of permutations of $n$ distinct objects taken $k$ at a time, expressed as $_{n} P_{k}$ , can be computed as follows:

$_{n} P_{k} = \frac{n!}{(n - k)} = (n) (n - 1) \dots (n - k + 1)$

Example 3. How many ways can you select three books from five books and arrange them on a shelf?

$_{5} P_{3} = \frac{5!}{(5 - 3)!} = \frac{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{2 \cdot 1} = 60$

Example 4. Show the calculations for the number of permutations of 25 distinct objects taken 4 at a time.

$\begin{matrix} _{5} P_{3} = \frac{25!}{(25 - 4)!} = \frac{25!}{21!} = \frac{25 \cdot 24 \cdot 23 \cdot 22 \cdot 21!}{21!} \\ = 303, 606 \end{matrix}$

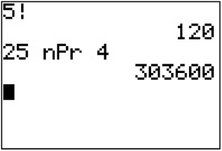
Calculator Note: TI-84 graphing calculators will compute both factorials and permutations. Here are the steps for using a TI-84 to compute the answers to Examples 1 and 4:

To compute 5!:

Press $\begin{matrix} 5 \end{matrix}$ .
Press $\begin{matrix} MATH \end{matrix}$ , highlight PRB, and press $\begin{matrix} 4 \end{matrix}$ (for !).
Press $\begin{matrix} ENTER \end{matrix}$ to complete the calculation.

To compute $_{25} P_{4}$ :

Press $\begin{matrix} 5 \end{matrix}$ .
Press $\begin{matrix} MATH \end{matrix}$ , highlight PRB, and press $\begin{matrix} 2 \end{matrix}$ (for $_{n} P_{r}$ ).
Press $\begin{matrix} 4 \end{matrix}$ followed by $\begin{matrix} ENTER \end{matrix}$ .

The output below shows the screen from the TI-84 after performing these two calculations.

Practice Exercises

Calculate the following showing the mathematical steps needed for the calculation. (In other words, do not use the built-in calculator functions for factorials or permutations.)

8!
$_{15} P_{5}$
$_{30} P_{2}$
$_{27} P_{3}$
Use your calculator’s built-in function for $_{n} P_{k}$ to calculate $_{50} P_{10}$ .

B. Combinations

A combination is a selection of a subset of a specific size, say $k$ , from a set of $n$ distinct elements where the order of the selection does not matter. We can express the number of combinations as $_{n} C_{k}$ , which is often pronounced as “ $n$ choose $k$ .”

Example 1. Suppose you have five books and want to choose three of the five to give to a friend as a gift. How many possible ways can this gift be selected?

In Example 3 in Algebra Review VIII, item A, Permutations (above), we calculated the number of ways that we could select three books out of five and arrange them: $_{5} P_{3} = 60$ . But here, the order of the selection does not matter—the selected books will all go in the same gift box. So Book A, Book B, and Book C is the same gift as Book C, Book B, and Book A. There are 3! arrangements of the three selected books. So our answer should be $_{5} P_{3} / 3! = \frac{60}{6} = 10$ .

Page AR-30

The number of ways to choose $k$ distinct objects from $n$ distinct objects (where the order of the selection does not matter) is

$_{n} C_{k} = \frac{_{n} P_{k}}{k!} = \frac{n!}{(n - k)! k!}$

Example 2. Find the number of possible ways to choose a three-person committee from a club with 50 members.

$\begin{matrix} _{50} C_{3} = \frac{50!}{(50 - 3)! 3!} = \frac{50 \cdot 49 \cdot 48 \cdot 47!}{47! 3!} \\ = \frac{\overset{25}{\overset{︷}{50}} \cdot 49 \cdot \overset{16}{\overset{︷}{48}}}{3 \cdot 2 \cdot 1} = 25 \cdot 49 \cdot 16 = 19, 600 \end{matrix}$

Example 3. Show the calculations for $_{25} C_{4}$ . Compare its value with $_{25} P_{4}$ in Example 4 from Algebra Review VIII, item A, Permutations (page AR-29).

$\begin{matrix} _{25} C_{4} = \frac{25!}{(25 - 1)! 4!} = \frac{25 \cdot 24 \cdot 23 \cdot 22 \cdot 21}{21! 4!} \\ = \frac{25 \cdot 24 \cdot 23 \cdot 22}{4 \cdot 3 \cdot 2 \cdot 1} = 22 \cdot 23 \cdot 22 = 12, 650 \\ _{25} P_{4} = 303, 600 which is 4! \times_{25} C_{4} or 24 \times_{25} C_{4} \end{matrix}$

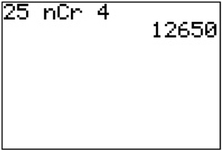
Calculator Note: TI-84 graphing calculators will compute combinations. Here are the steps for using a TI-84 to compute $_{25} C_{4}$ from Example 3:

Press $\begin{matrix} 2 \end{matrix} \begin{matrix} 5 \end{matrix}$ .
Press $\begin{matrix} MATH \end{matrix}$ , highlight PRB, and press $\begin{matrix} 3 \end{matrix}$ (for $_{n} C_{r}$ ).
Press $\begin{matrix} 4 \end{matrix}$ . followed by $\begin{matrix} ENTER \end{matrix}$ .

Practice Exercises

Calculate the following showing the mathematical steps needed for the calculation. (In other words, do not use the built-in calculator function for combinations.)

$_{15} C_{5}$
$_{30} C_{2}$
$_{27} C_{3}$
$_{50} C_{10}$
Use your calculator’s built-in function for $_{n} C_{k}$ to calculate $_{50} C_{20}$ .