9.4 9.3 Other Voting Systems for Three or More Candidates
With three or more candidates, we find no shortage of additional procedures that suggest themselves and that seem to represent perfectly reasonable ways to choose a winner. Closer inspection, however, reveals shortcomings with all of these. We illustrate this with a consideration of several well-known procedures. Additional procedures (and additional shortcomings) can be found in the exercises.
Plurality Voting and the Condorcet Winner Criterion
In plurality voting, only first-place votes are considered. Thus, while we will consider plurality voting in the context of preference list ballots, a ballot here might just as well be a single vote for a single candidate. The candidate with the most votes wins, even though this may be considerably fewer than one-half the total votes cast. This is perhaps the most common system in use today. It is how the voters in Florida chose George W. Bush over Al Gore, Ralph Nader, and Patrick J. Buchanan in the presidential election of 2000.
EXAMPLE 3 Plurality Voting and the 2000 Presidential Election
Plurality Voting and the 2000 Presidential Election
On the evening of December 12, 2000, Al Gore conceded the presidential election of 2000 to George W. Bush, thus bringing to a close one of the most remarkable elections in modern times. The outcome, ultimately decided in the Electoral College, came down to whether Bush or Gore would carry Florida. With more than 6 million votes cast in Florida, the ultimate margin of victory for George W. Bush was only a few hundred votes.
There is little doubt that if the 2000 presidential election had pitted Al Gore solely against any one of the other three candidates, then Gore would have won both the election in Florida and the presidency. The point is that while most of the Buchanan supporters probably would have voted for Bush, the far more numerous Nader supporters probably would have gone largely for Gore. In fact, the illustration of Condorcet’s method that we gave in Example 2 is a simplified version of this Florida election (with GB standing for George Bush, AG for Al Gore, PB for Patrick Buchanan, and RN for Ralph Nader).
Thus, although plurality voting led to Bush’s winning the 2000 election in Florida (and hence the presidency), Gore was, in this example, what is called a Condorcet winner: He would have won the election if Condorcet’s method had been used.

Condorcet Winner Criterion DEFINITION
A voting system is said to satisfy the Condorcet winner criterion (CWC) provided that, for every possible sequence of preference list ballots, either (1) there is no Condorcet winner (as is often the case) or (2) the voting system produces exactly the same winner for this election as does Condorcet’s method.
The CWC is certainly a property that one would like to see satisfied. We record plurality voting’s failure in this respect with the following.
The Failure of the CWC with Plurality Voting THEOREM
The Florida vote in the 2000 presidential election shows that plurality voting fails to satisfy the CWC.
Perhaps a more fundamental drawback of plurality voting is the extent to which the ballots provide no opportunity for a voter to express any preferences except for naming his or her top choice. No use is made, for example, of the fact that a candidate may be no one’s first choice but everyone’s close second choice.
To illustrate this point, we return to the mathematics department’s five-person hiring committee that has interviewed four candidates: Adam, Beth, Carol, and Dan. They have ranked the candidates on their five ballots (reproduced in the table below), but now, let’s suppose that instead of using Condorcet’s method, they decide to use plurality.
EXAMPLE 4 Plurality Voting
Plurality Voting
| Number of Voters (5) | |||||
|---|---|---|---|---|---|
| Rank | Voter 1 | Voter 2 | Voter 3 | Voter 4 | Voter 5 |
| First | Adam | Dan | Carol | Adam | Beth |
| Second | Beth | Carol | Beth | Carol | Dan |
| Third | Carol | Beth | Dan | Dan | Carol |
| Fourth | Dan | Adam | Adam | Beth | Adam |
Clearly, Adam wins with the plurality method because he received two first-place votes and each of the others received only one. But 60% of the voters (i.e., three of the five voters) rank Adam last!
Finally, there is yet another shortcoming of plurality voting: There are elections in which it is to a voter’s advantage to submit a ballot that misrepresents his or her true preferences.
Manipulability DEFINITION
A voting system is subject to manipulability (or is manipulable) if there are elections in which it is to a voter’s advantage to submit a ballot that misrepresents his or her true preferences.
Self Check 3
Suppose there is an election in which a voter can change the outcome of an election to one he prefers less by submitting a disingenuous ballot. Does this mean the voting system is manipulable (according to the above definition)?
- No. According to the definition, a voting system is manipulable only if there is an election in which a voter gets a more preferred outcome (rather than a less preferred outcome) by submitting a disingenuous ballot.
In the presidential election of 2000, many voters who ranked Ralph Nader or Patrick J. Buchanan over George W. Bush and Al Gore chose to vote for Bush or Gore rather than to “throw away” their vote on a candidate they believed had no chance. Condorcet’s method, it turns out, is not manipulable, and this is one of its most desirable properties. We’ll explore this further in the next chapter.
The Borda Count and Independence of Irrelevant Alternatives
In many elections that use preference list ballots, the goal is to arrive at a final group rank ordering of all the contestants that best expresses the desires of the electorate. The purpose is not only to determine the winner—say, the class valedictorian—but also to arrive at who finished second, third, and so on, as in the case of one’s rank in the senior class. In other applications, such as an election to a hall of fame, the first few finishers each win, while the remaining nominees are also-rans.
One common mechanism for achieving this objective is to assign points to each voter’s rankings and then to sum these for all voters to obtain the total points for each candidate. If there are 10 candidates, for example, then we could assign 9 points to each first-place vote for a given candidate, 8 points for each second- place vote, 7 for each third-place vote, and so forth. The candidate with the highest total number of points is the winner. Subsequent positions are assigned to those with the next-highest tallies.
Description of Rank Methods and the Borda Count PROCEDURE
A rank method of voting assigns points in a non-increasing manner to the ordered candidates on each voter’s preference list ballot and then sums these points to arrive at a group’s final ranking. The special case in which there are n candidates with each first-place vote worth n−1 points, each second-place vote worth n−2 points, and so on down to each last-place vote worth 0 points is known as the Borda count. The actual point totals are referred to as a candidate’s Borda score.
The Borda count is named after Jean-Charles de Borda (1733–1799), who was a contemporary of Condorcet.
Rank methods other than the Borda count are common. For example, a track meet can be thought of as an “election” in which each event is a “voter” and each of the schools competing is a “candidate.” If the order of finish in the 100-meter dash is school A, school B, school C, school D, then points are often awarded to each school as follows: 5 points for first place, 3 for second place, 2 for third place, and 1 for fourth place.
Sports polls often use point assignments that qualify as rank methods according to our definition. The following example provides an illustration of this.
EXAMPLE 5 Rank Methods and a Basketball Poll
Rank Methods and a Basketball Poll
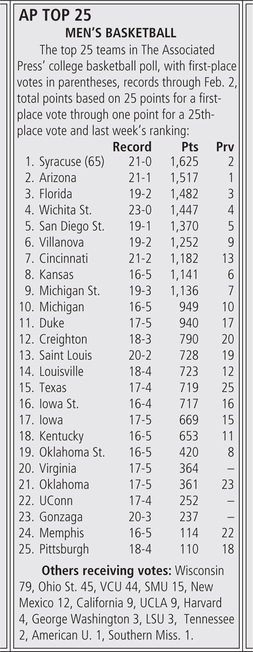
In February 2014, the Associated Press issued its weekly ranking of the top 25 teams in men’s college basketball, shown at right.
An interesting question is whether or not this is a ranking system. If it is, who are the candidates and how many are there? In fact, this can be regarded as a ranking system, but the number of candidates is not 25. That is, although 25 teams appeared on each ballot, at least one ballot included each of the teams listed at the bottom in the category “Others receiving votes.”
For this to be regarded as a ranking system, the set of candidates must include the entire set of eligible collegiate men’s basketball teams. We must also infer that each ballot lists all teams other than that voter’s top 25 below that voter’s top 25, perhaps in alphabetical order. The point assignments are then like those in the newspaper clipping, except that we also assign 0 points for a 26th place vote, 0 points for a 27th place vote, and so on. This is why our definition states that a rank method “assigns points in a nonincreasing manner” instead of “assigns points in a decreasing manner.”
We can use this poll to illustrate how total points are arrived at with a ranking method. With the top-ranked team, Syracuse, it’s quite easy. Each first-place vote is worth 25, and Syracuse received all 65 first-place votes. This accounts for its total of 25×65=1625 points. But the calculation is more interesting for the second-ranked team, Arizona, and requires some speculation on our part because we don’t actually have the ballots to examine. We know that there were 65 ballots (because there were exactly 65 first-place votes altogether), and we know that Arizona had no first-place votes. It stands to reason that Arizona’s 1517 points must have come from a vast majority of the second-place votes, together with a few lower rankings. (We know that the team didn’t receive all the second place-votes; otherwise, its point total would have been 24×65=1560.)

One possibility is that Arizona received:
- 0 first-place votes (at 25 points each)
- 40 second-place votes (at 24 points each)
- 15 third-place votes (at 23 points each)
- 4 fourth-place votes (at 22 points each)
- 4 fifth-place votes (at 21 points)
- 2 sixth-place votes (at 20 points)
The total would then be
0+960+345+88+84+40=1517
Self Check 4
Suppose Arizona received 39 second-place votes (instead of 40) and 3 fourth-place votes (instead of 4). What must the number of third-place votes be if no other change is made and the total for Arizona is still 1517?
- Arizona would have lost 24 points (for losing a second-place vote) and 22 points (for losing a fourth- place vote), for a total loss of 46 points. Hence, if Arizona received 17 third-place votes instead of 15, it would gain back the 46 lost points and still have a total of 1517.
There is an easy way to calculate the Borda score of a candidate. You can count the number of occurrences of other candidate names that are below this candidate’s name. For example, consider the following ballots:
| Rank | Number of Voters (5) | Points | ||||
|---|---|---|---|---|---|---|
| First | A | A | A | B | B | 2 |
| Second | B | B | B | C | C | 1 |
| Third | C | C | C | A | A | 0 |
Because there are three candidates, each first-place vote is n−1, or 3−1=2; each second-place vote is n−2=1; and each third-place vote is n−3=0. If we were to calculate the Borda score of Candidate B algebraically, we would say that B has two first-place votes, worth 2 points each (a total of 4 points), and three second-place votes, worth 1 point each (a total of 3 more points). Thus, the Borda score of Candidate B is 4+3=7.
But instead of calculating this Borda score algebraically, we can mentally replace each occurrence of a letter below B by a box, □, and simply count the boxes.
| Rank | Number of Voters (5) | ||||
| First | A | A | A | B | B |
| Second | B | B | B | □ | □ |
| Third | □ | □ | □ | □ | □ |
Notice that there are seven boxes, giving us the correct value of 7 as the Borda score for Candidate B. Of course, you don’t actually have to draw any boxes. We are just emphasizing the fact that, in the counting process, it is “spaces” that we are counting, without regard to which letter occurs in the space. A quick glance at the original ballots (without the boxes) reveals that the Borda score of Candidate A is 6 and the Borda score of Candidate C is 2. When calculating Borda scores this way, be sure that each individual ballot is listed separately, as opposed to using a single list to represent the ballots of several voters (as we often do).
The Borda count certainly seems to be a reasonable way to choose a winner from among several candidates (or to arrive at a group ranking of the candidates). It also has its shortcomings, however, one of which is the failure of a property known as independence of irrelevant alternatives (IIA).
Independence of Irrelevant Alternatives DEFINITION
A voting system is said to satisfy independence of irrelevant alternatives (IIA) if it is impossible for a Candidate X to move from nonwinner status to winner status unless at least one voter reverses the order in which he or she had X and the winning candidate ranked.
To describe this property, suppose that an election yields one candidate (call it A) as a winner and another candidate (call it B) as a nonwinner. Suppose that a new election is now held and that, although some of the voters may have changed their preference list ballots, no one who had previously ranked A over B changed his or her ballot to rank B over A now.
If this new election were to yield B as a winner, the new outcome would seem strange, especially because not one of the relative individual preferences for A over B had changed in B’s favor. The ballot changes responsible for the new outcome involve candidates other than A or B. One could argue that these other candidates ought to be “irrelevant” to the question of whether A is more desirable than B or B is more desirable than A. This inspires the name “independence of irrelevant alternatives.”
Condorcet’s method satisfies IIA. That is, if we have a sequence of preference list ballots that yield A as a Condorcet winner and B as a nonwinner, then A defeats every other candidate, and B in particular, in a one-on-one contest according to these ballots. If no voter reverses the order in which he or she ranked A and B, then A will still defeat B one on one, and thus B remains a nonwinner.
The following illustration shows that the Borda count, unlike Condorcet’s method, fails to satisfy IIA. Suppose the initial five ballots are as follows:
| Rank | Number of Voters (5) | ||||
|---|---|---|---|---|---|
| First | A | A | A | C | C |
| Second | B | B | B | B | B |
| Third | C | C | C | A | A |
Our counting procedure shows that the Borda scores are as follows:
- Borda score of A is 6.
- Borda score of B is 5.
- Borda score of C is 4.
The winner is A (with 6 points), and B is a nonwinner (with 5 points). But now suppose that the two voters on the right change their ballots by moving C down between A and B. The ballots then become:
| Rank | Number of Voters (5) | ||||
|---|---|---|---|---|---|
| First | A | A | A | B | B |
| Second | B | B | B | C | C |
| Third | C | C | C | A | A |
Our counting procedure shows that the Borda scores are as follows:
- The Borda score of A is 6.
- The Borda score of B is 7.
- The Borda score of C is 2.
The Borda count therefore now yields B as the winner (with 7 points). Thus, B has gone from being a nonwinner to being a winner, even though no one changed his or her mind about whether B is preferred to A, or vice versa. Hence, the fact that A wins and B loses is not “independent” of where the “irrelevant” alternative C is ranked.
The above discussion establishes the following theorem.
The Failure of IIA with the Borda Count THEOREM
The Borda count fails to satisfy IIA.
Sequential Pairwise Voting and the Pareto Condition
In our voting-theoretic context, an agenda will be understood to be a listing (in some order) of the candidates. This listing is not to be confused with any of the preference list ballots, and to avoid confusion, we will present agendas as horizontal lists and continue to present preference list ballots vertically.
Description of Sequential Pairwise Voting PROCEDURE
Sequential pairwise voting starts with an agenda and pits the first candidate against the second in a one-on-one contest. The winner then moves on to confront the third candidate in the list, one on one. Losers are deleted. This process continues throughout the entire agenda, and the one remaining at the end wins.
For a given sequence of individual preference list ballots, the particular agenda chosen can greatly affect the outcome of the election, as we’ll show in the next chapter. Nevertheless, we will see later in this chapter that sequential pairwise voting arises naturally in the legislative process. Notice also that because of our assumption that the number of voters is odd, there is always a unique winner with sequential pairwise voting.
EXAMPLE 6 Sequential Pairwise Voting
Sequential Pairwise Voting
Assume we have four candidates and that the agenda is A, B, C, D. Consider the following sequence of three preference list ballots:
| Rank | Number of Voters (3) | ||
|---|---|---|---|
| First | D | B | C |
| Second | C | D | A |
| Third | A | C | B |
| Fourth | B | A | D |
The first one-on-one pits A against B, and A wins by a score of 2 to 1 (meaning that two of the voters—the two not in the middle—prefer A to B, and one of the voters prefers B to A). Thus, B is eliminated and A moves on to confront C. Because C wins this one on one (by a score of 3 to 0), A is eliminated. Finally, C takes on D, and D wins by a score of 2 to 1. Thus, D is the winner.
Self Check 5
Is Candidate D a Condorcet winner in this example?
- No, Candidate D is not a Condorcet winner, because D loses to B in a one-on-one contest.
EXAMPLE 7 Sequential Pairwise Voting (with a different agenda)
Sequential Pairwise Voting (with a different agenda)
Assume we have the same ballots as in Example 6, but now let’s use sequential pairwise voting with the agenda D, C, B, A. The first one-on-one pits D against C, and D wins by a score of 2 to 1 (as only the third voter ranked C over D). Thus, C is eliminated and D moves on to confront B. Because B wins this one-on-one (by a score of 2 to 1), D is eliminated. Finally, B takes on A, and A wins by a score of 2 to 1. Thus, A is the winner.
Self Check 6
Is Candidate A a Condorcet winner in this example?
- No, Candidate A is not a Condorcet winner, because A loses to C (and, incidentally, to D as well) in a one-on- one contest.
There is something very troubling about the outcome of the preceding example, especially if you are Candidate C. Everyone prefers C to A, but A ends up winning! This example shows that sequential pairwise voting fails to satisfy what is called the Pareto condition.
Pareto Condition DEFINITION
A voting system is said to satisfy the Pareto condition provided that in every election in which every voter prefers one candidate X to another candidate Y, the latter candidate Y is not among the winners.
Self Check 7
Suppose a voting system satisfies the Pareto condition and we have an election in which every voter prefers Candidate X to Candidate Y. Is Candidate X definitely among the winners (“yes” or “no”)?
- No. An example is given in the text on page 419.
Again, the Pareto condition (named after Italian economist Vilfredo Pareto, 1848–1923) is a property we would like to see satisfied. But Example 6 (with Candidate B in the role of X and Candidate D in the role of Y) establishes the following.
The Failure of the Pareto Condition with Sequential Pairwise Voting THEOREM
Sequential pairwise voting fails to satisfy the Pareto condition.
The following sequence of three preference list ballots illustrates the Pareto condition further:
| Rank | Number of Voters (3) | ||
|---|---|---|---|
| First | C | C | A |
| Second | A | A | B |
| Third | B | B | C |
Every one of the three voters prefers A to B. Hence, if we were using a voting rule that satisfies Pareto, we would conclude that B is not among the winners. However, we cannot conclude that A is among the winners. Indeed, there are very reasonable voting rules, like plurality, that satisfy the Pareto condition but would produce C as the unique winner using these ballots.
Runoff Systems and Monotonicity
The voting system known as the Hare system, which was introduced by Thomas Hare in 1861, is also known by names such as the “single transferable vote system.” In 1862, John Stuart Mill described the Hare system as being “among the greatest improvements yet made in the theory and practice of government.” Today, the system is used to elect public officials in Australia, Malta, the Republic of Ireland, and Northern Ireland.
Description of the Hare System PROCEDURE
The Hare system proceeds to arrive at a winner by repeatedly deleting candidates that are “least preferred” in the sense of being at the top of the fewest ballots. If a single candidate remains after all others have been eliminated, he or she alone is the winner. If two or more candidates remain and all of these remaining candidates would be eliminated in the next round (because they all have the same number of first-place votes), then these candidates are declared to be tied for the win.
EXAMPLE 8 The Hare System
The Hare System
Suppose we have the following sequence of preference list ballots:
| Rank | Number of Voters (5) | ||||
|---|---|---|---|---|---|
| First | A | A | B | B | C |
| Second | C | C | C | C | A |
| Third | B | B | A | A | B |
Candidate C has only 1 first-place vote (while B and A have 2 each). Thus, C is eliminated in round 1, and the ballots for the second round are as follows:
| Rank | Number of Voters (5) | ||||
|---|---|---|---|---|---|
| First | A | A | B | B | A |
| Second | B | B | A | A | B |
In the second round, B has only 2 first-place votes (while A has 3), so B is eliminated in round 2. Because A is the only candidate left, he or she is the unique winner of this election.
We now give another example of the Hare system. It is a bit more complicated than Example 8, but as with earlier examples in this section, it will reveal a serious shortcoming of a seemingly very reasonable voting system (the Hare system, in this case).
EXAMPLE 9 Shortcomings of the Hare System
Shortcomings of the Hare System
Suppose we have the following sequence of preference list ballots, where, as before, the heading of “5” indicates that 5 of the 13 voters hold the ballot with A over B over C, the heading of “4” indicates that 4 of the 13 voters hold the ballot with C over B over A, and so forth.
| Number of Voters (13) | ||||
|---|---|---|---|---|
| Rank | 5 | 4 | 3 | 1 |
| First | A | C | B | B |
| Second | B | B | C | A |
| Third | C | A | A | C |
Candidates B and C have only 4 first-place votes (while A has 5). Thus, B and C are eliminated in the first round, and A wins the election.
Now, suppose that the voter in the last column moves Candidate A up on his list. Let’s look at the new election. Notice that, even though A won the last election, the only change we are making in ballots for the new election is one that is favorable to A. The ballots for the new election are as follows:
| Number of Voters (13) | ||||
|---|---|---|---|---|
| Rank | 5 | 4 | 3 | 1 |
| First | A | C | B | A |
| Second | B | B | C | B |
| Third | C | A | A | C |
If we apply the Hare system again, only B is eliminated in round 1, as he or she has 3 first-place votes, as opposed to 4 for C and 6 for A. Thus, after this round, the ballots are as follows:
| Number of Voters (13) | ||||
|---|---|---|---|---|
| Rank | 5 | 4 | 3 | 1 |
| First | A | C | C | A |
| Second | C | A | A | C |
We now have A on top of 6 lists and C on top of 7 lists. Thus, at stage 2, A (our previous winner!) is eliminated and C is the winner of this new election.
Clearly, this is once again quite counterintuitive. Alternative A won the original election, the only change in ballots made was one favorable to A (and no one else), and then A lost the next election. This example shows that the Hare system fails to satisfy what is called monotonicity.
Monotonicity DEFINITION
A voting system for three or more candidates is said to satisfy monotonicity provided that, for every election, if some candidate X is a winner and a new election is held in which the only ballot change made is for some voter to move this winning candidate X higher on his or her ballot (and to make no other changes), then X will remain a winner.
As with the CWC and the Pareto condition, monotonicity is a property we would like to see satisfied. But Example 9 (with Candidate A in the role of X) establishes the following.
The Failure of Monotonicity with the Hare System THEOREM
The Hare system fails to satisfy monotonicity.
The fact that the Hare system does not satisfy monotonicity is considered by many—and with good reason—to be a glaring defect. A 17-voter example in which only a single candidate is eliminated in the first round can also be used to show that the Hare system does not satisfy monotonicity (see Exercise 28 on page 436). For an even more glaring version of this defect, one in which alternative A goes from winning to losing because voters move A from last place on their ballots to first place on their ballots, see Exercise 29 (page 436).
In spite of these drawbacks, the Hare system is used in important ways today. For example, it is essentially the method that was used to choose Rio de Janeiro as the site of the 2016 Summer Olympics. Chicago was eliminated in the first round on the basis of fewest first-place votes, then Tokyo in the second round, and Madrid in the final round.
There are other runoff systems, some more frequently used than the Hare system. One such example is the following.
Description of the Plurality Runoff Method PROCEDURE
Plurality runoff is the voting system in which there is a runoff (i.e., a new election using the same ballots) between the two candidates receiving the most first-place votes. If there are ties, then the runoff is among either those tied for the most first- place votes, or the lone candidate with the most first-place votes along with those tied for the second-most first-place votes (and plurality voting is used).
EXAMPLE 10 Plurality Runoff
Plurality Runoff
The plurality runoff method is somewhat similar in spirit to the Hare system. In fact, you might wonder if they aren’t just two different descriptions of the same voting system. That is, you might ask if the plurality runoff method and the Hare system always yield the same winner.
The answer is “no,” however, as we now demonstrate. Consider the following sequence of preference list ballots:
| Number of Voters (13) | ||||
|---|---|---|---|---|
| Rank | 4 | 4 | 3 | 2 |
| First | A | B | C | D |
| Second | B | A | D | C |
| Third | C | C | A | A |
| Fourth | D | D | B | B |
With the plurality runoff method, A and B initially tie with 4 first-place votes each, with 3 for C and 2 for D. In the runoff between A and B, the ballots are as follows:
| Number of Voters (13) | ||||
|---|---|---|---|---|
| Rank | 4 | 4 | 3 | 2 |
| First | A | B | A | A |
| Second | B | A | B | B |
With the plurality runoff method, A is the winner, defeating B in the runoff by a score of 9 to 4.
On the other hand, with the Hare system, we find that the only alternative deleted in the first round is D, with only 2 first-place votes. With this deletion of D, the ballots are as follows:
| Number of Voters (13) | ||||
|---|---|---|---|---|
| Rank | 4 | 4 | 3 | 2 |
| First | A | B | C | C |
| Second | B | A | A | A |
| Third | C | C | B | B |
A and B now have only 4 first-place votes compared to the 5 first-place votes that C has. Hence, A and B are now deleted, leaving C as the winner with the Hare system.
Alas, the plurality runoff method also does not satisfy monotonicity. Exercise 25 (page 435) asks you to verify this.