4 How Pegs Break II: Contingent Monetary Policies

In the previous section, we found that inconsistent fiscal policies under a fixed exchange rate regime eventually cause an exchange rate crisis. However, the crises of the 1990s often did not conform to a model based on deficit monetization because budget problems were absent in many cases. In particular, the Exchange Rate Mechanism (ERM) crisis of 1992 affected developed countries in Europe, most of which were unlikely to monetize deficits. In countries with apparently sound economic policies, foreign currency speculators went for the attack and pegs broke.22

Economists therefore developed alternative models of crises, with the pioneering work on the second-generation crisis model being done by Maurice Obstfeld. These types of models can explain how, even when policy making is rational and purposeful—rather than incompetent and inconsistent—there may still be situations in which pegs break for no apparent reason.23

The Basic Problem: Contingent Commitment

The essence of the model is that policy makers are not committed to the peg under all circumstances. Defending the peg is therefore a contingent commitment (a slight oxymoron): if things get “bad enough,” the government will let the exchange rate float rather than put the country through serious economic pain. The problem is that everyone—especially, investors in the forex market—knows this and will adjust their expectations accordingly.

To develop some intuition, we return to Britain and Germany in 1992, the example we saw at the start of the previous chapter when we studied fixed and floating regimes. Let’s recap the basic story: the German central bank raised interest rates to deal with a domestic shock, the fiscal expansion arising from German unification after 1989. This left Britain with a higher interest rate and a lower output level than it wanted. What would Britain do in response?

If German interest rates are fairly low, so too are British interest rates, output costs in Britain are low, and nobody expects Britain to leave the peg. The peg is credible. But if German interest rates rise to high levels, output in Britain falls to an intolerably low level, and nobody expects Britain to stay on the peg for long. Instead, everyone thinks Britain will float and use expansionary monetary policy to boost output and depreciate the pound. The peg is not credible, and the market now expects a depreciation in the future.

The problem for Britain is that an expected depreciation will introduce a currency premium, as we saw earlier in this chapter. Investors will demand even higher interest rates in Britain to compensate for the imminent depreciation—and this will mean even lower output and even higher pain for Britain!

This creates a gray area. How? It is quite possible that the German interest rate can be at some “intermediate” level at which pegging is tolerable with no expected depreciation: people would expect the peg to hold and the peg would hold. But if there is an expected depreciation and a currency premium, pegging might be intolerable: people would expect the peg to fail and the peg would fail. Crucially, in both scenarios, ex ante market expectations are validated ex post, and hence would be considered “rational.”

Based on these insights from the Britain-Germany example, we now develop an economic model with such self-fulfilling expectations. In this model we may not always find a single, unique equilibrium but rather multiple equilibria. Whether there is a crisis depends entirely on market sentiment, and not simply economic fundamentals.

A Simple Model

In this type of model, we need a measure of the cost of maintaining the peg. The simplest cost measure is the deviation of output Y in the short run below its full employment level. To allow output to vary, we need to use the IS-LM-FX model introduced in the chapter on macroeconomic policy, which means that we reverse some of the assumptions we made before. From now on, output Y will be variable rather than fixed, and it will be determined by the model. And from now on, prices will be sticky, not flexible, and treated as given.24

For simplicity, we assume there are some benefits from pegging, say, the gains from increased trade. Let these benefits be b > 0 and constant. Against the benefits of pegging, the government weighs costs c that equal the “output gap”: full-employment output minus current output Y. If costs exceed benefits, we assume that the government will elect to float next period and use monetary policy to restore full employment output. For simplicity, we assume each period lasts one year. (Restricting attention to this type of rule keep things simple while illustrating the key trade-offs.)

In Figure 20-16, we use the home IS-LM-FX diagram to look at how outcomes under the peg can depend on both economic fundamentals and market expectations. We assume foreign output is fixed at Y*, and we also assume there is no fiscal policy change, so we can focus only on home monetary policy choices. Most important, we assume that investors are aware of the contingent commitment to the peg.

In this setup, it does not matter where adverse output shocks originate. They could result from increases in the foreign interest rate (as in the ERM example). Or they could be caused by a decline in the demand for home goods overseas. All that matters is that the home economy is in some kind of pain with output below the desired level.

Small Recession, Peg Credible Panel (a) shows a situation in which the pain is small. Initially, the IS₁ and LM₁ curves intersect at equilibrium point 1, and the home interest rate is i₁ = i* to maintain the peg. In the FX diagram, the domestic return is DR₁ and the foreign return FR₁. They intersect at point 1′ and the exchange rate is fixed at E₁ = 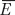. Home output is at Y₁, but we assume that the desired full employment level of home output is , slightly higher than Y₁. In this situation, when the peg is credible, the economy suffers a small cost given by the “output gap”: c₁ = − Y₁.

Large Recession, Peg Credible Panel (b) shows a situation in which the adverse shock to output is large. The IS₂ and LM₂ curves now intersect at equilibrium point 2. The IS curve has moved left by assumption: it is the source of the adverse shock. The LM curve has moved in to maintain the peg and preserve interest parity, so that the home interest rate remains at i₁ = i*. In the FX diagram, the domestic return is still DR₁ and the foreign return is still FR₁, and they intersect at point 2′, the same as point 1′, with E₁ = 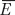. Home output is now much lower at Y₂. Here, the economy suffers an even larger cost given by the “output gap”: c₂ = − Y₂.

We obtain our first important result: if the market believes that the peg is credible, the output gap (cost) increases as the size of the adverse shock increases.

Large Recession, Peg Not Credible This is the most complex situation. Panel (c) assumes a large recession as in panel (b), but shows what happens if investors believe that the authorities will choose to depreciate next year to achieve desired output. We suppose exchange rate expectations are unchanged next year at the pegged rate. The IS curve will still be at IS₂, and the required monetary expansion next year will shift the LM curve to LM₄ so that the new equilibrium will be at point 4 with output at the desired level , and a low interest rate of i₄. This will lead to a temporary depreciation next year, the peg will break, and the exchange rate will rise from 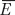to E_float. We can also see that to achieve full employment output, the lower that Y₂ is, the larger the required shift in the LM curve will be next year and the larger the resulting depreciation.

However, the government’s response next year will be anticipated by investors. If they know that output is low enough to prompt a depreciation, they will expect a depreciation over the coming year of a size given by . This expected depreciation will appear today as a currency premium in the FX market of panel (c). The current period’s risk-adjusted foreign return curve shifts up to FR₂ by an amount equal to the currency premium.

If the central bank wants to maintain the peg, even though it is not credible, it has to ensure forex market equilibrium at point 3′, so it must raise the home interest rate to i₃. At today’s pegged rate 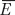, uncovered interest parity now requires a higher home interest rate 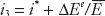. Graphically, this means the domestic return curve must also shift up (to DR₂) by an amount equal to the currency premium.

As we know from the earlier chapters on policy and regimes, this shift will depress home demand and lead to even lower home output today, which is shown at Y₃.

In more detail, today the IS curve moves out slightly to IS₃ due to expected depreciation, but the LM curve moves in a long way to LM₃ to defend the peg. The latter effect dominates, because we know that demand and output have to be lower today given the combination of the same exchange rate (no change in the trade balance) and a higher interest rate (lower investment demand). So the new IS-LM equilibrium is at point 3, to the left of point 2.

We also note that to achieve this monetary contraction, the central bank must sell reserves—and the drain can take the form of a speculative attack if the currency premium appears suddenly as a result of a switch in beliefs.

The loss of credibility makes a bad recession even worse. If the peg is not credible, a higher interest rate causes the costs of pegging to rise to c₃ = − Y₃. Finally, we note that this cost will be higher when the output gap is higher, because a larger output gap implies a larger depreciation to restore full employment.

Our second important result: if the forex market switches to believing that the peg is not credible, then reserves drain, the interest rate rises, and the output gap (cost) increases; also, the cost increases more if the output gap is larger to begin with.

The Costs and Benefits of Pegging Our IS-LM-FX analysis is now complete, and all we need to do is consider the implications.

Figure 20-17 sums up the cost–benefit analysis. The horizontal axis measures the output gap, or the cost of pegging, when the peg is credible. We denote these costs c(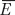). This notation indicates that this is the cost c when the exchange rate is expected to be at 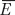next period. The first of our results showed that this cost rises, and we move right along the horizontal axis, whenever the country suffers an adverse shock under the peg.

The vertical axis measures and compares the costs and benefits of pegging. Benefits are constant at b. The costs when the peg is credible are equal to c(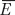) so these will fall on the 45-degree line, since c(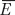) is measured on the horizontal axis.

Finally, the cost of pegging when the peg is not credible is denoted c(E_float). This notation indicates that this is the cost c when the exchange rate is expected to be at E_float next period.

The second of our results showed that the costs of pegging when the peg is not credible are always greater than the costs when the peg is credible, due to the rise in the currency premium associated with an expected depreciation. In other words, the c(E_float) line is above the c(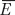) line, as shown. We also saw that the difference gets larger as the costs grow larger. In Figure 20-17, this means that the c(E_float) curve diverges from the c(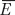) curve, as shown.

Corresponding to the previous analysis in Figure 20-16, point 1 (cost c₁) represents a small recession with a credible peg; point 2 (cost c₂) represents a large recession with a credible peg; point 3 (cost c₃) represents the same large recession with a noncredible peg.

With this basic apparatus, we can now analyze the “game” between the authorities and investors. To keep it simple, we suppose investors can choose from two beliefs about what the government will do: {peg, depreciate}. And we suppose the authorities then choose from two actions: {peg, depreciate}. Faced with this type of problem, economists search for what might be considered a rational outcome of the game. We look for a self-confirming equilibrium, that is, combinations of investor beliefs and government actions for which the ex post outcome validates the ex ante beliefs.

We can identify several such equilibria using Figure 20-17:

• In Zone I, b > c(E_float) > c(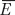), so the benefits b of pegging always outweigh both kinds of costs, no matter what the market believes. The authorities will always choose to “peg.” Anticipating this, the market belief will also be peg, and this is the only ex ante belief that will be validated ex post. Benefits are always given by b, and costs are always those of a credible peg c(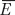). There is a unique self-confirming equilibrium: peg, with costs corresponding to the solid portion of the line c(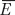). (Example: point 1.)
• In Zone III, c(E_float) > c(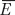) > b, so both kinds of costs of pegging always outweigh the benefits b, no matter what the market believes. The authorities will always choose to “depreciate.” Anticipating this, the market belief will also be depreciate, and this is the only ex ante belief that will be validated ex post. Benefits are then always given by b, and the costs are always those of a noncredible peg c(E_float). There is a unique self-confirming equilibrium: depreciate, with costs corresponding to the solid portion of the line c(E_float). (Example: point 5.)
• In Zone II, c(E_float) > b > c(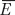). If the market belief is “depreciate,” then the benefits b of pegging are less than the costs of the noncredible peg c(E_float); authorities will then choose depreciate, and market beliefs are validated for this case. Conversely, if the market belief is peg, then the benefits b of pegging are greater than the costs of a credible peg c(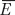); authorities will then choose peg, and the market beliefs are also validated for this case. There are two self-confirming equilibria in this zone. Zone II is shown as a gray area in the diagram. And appropriately so! In this range, there is no unique equilibrium, and depending on market beliefs, costs may correspond to the solid portions of either line c(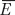) or line c(E_float). (Examples: points 2 and 3.)

Summary

Our results are striking. If government policies are contingent, then they will depend on market sentiment. But market sentiment, in turn, depends on what the market believes the government will do. If costs of pegging are “low,” then pegs hold when they “should”—when the government has no desire to exit. If costs of pegging are “high,” then crises happen when they “should”—when the government clearly wants to exit. But in between these extremes, an ambiguity arises in the form of multiple equilibria because for some “medium” range of costs, a crisis occurs if and only if the market expects a crisis.