1 Basics of Imperfect Competition

Monopolistic competition incorporates some aspects of a monopoly (firms have control over the prices they charge) and some aspects of perfect competition (many firms are selling). Before presenting the monopolistic competition model, it is useful to review the case of monopoly, which is a single firm selling a product. The monopoly firm faces the industry demand curve. After that, we briefly discuss the case of duopoly, when there are two firms selling a product. Our focus will be on the demand facing each of the two firms. Understanding what happens to demand in a duopoly will help us understand how demand is determined when there are many firms selling differentiated products, as occurs in monopolistic competition.

Monopoly Equilibrium

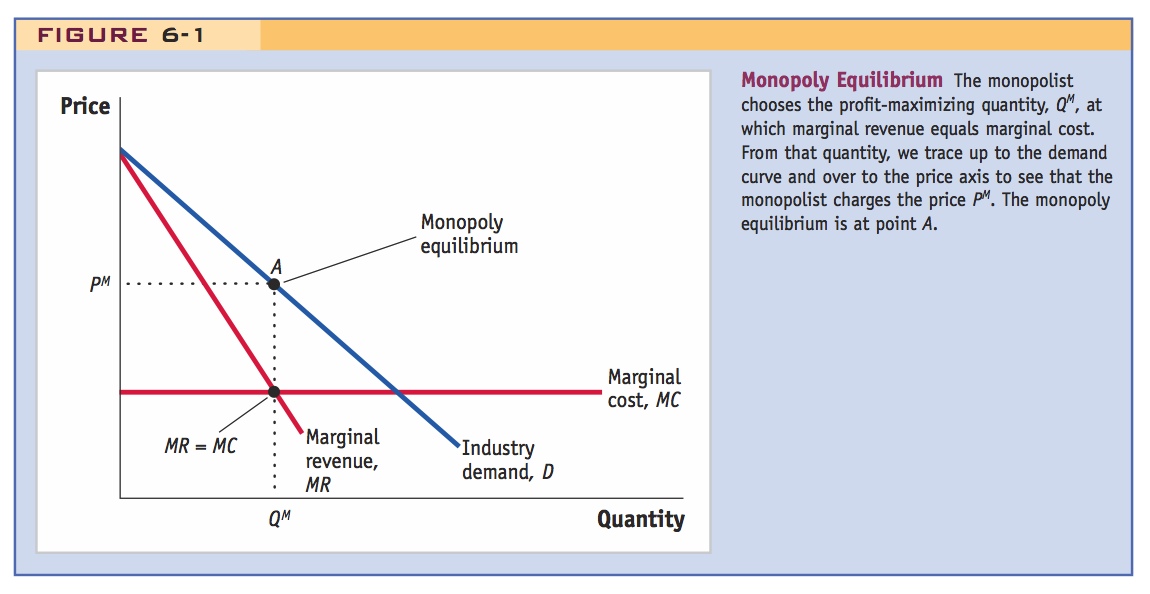
In Figure 6-1, the industry demand curve is shown by D. For the monopolist to sell more, the price must fall, and so the demand curve slopes downward. This fall in price means that the extra revenue earned by the monopolist from selling another unit is less than the price of that unit—the extra revenue earned equals the price charged for that unit minus the fall in price times the quantity sold of all earlier units. The extra revenue earned from selling one more unit is called the marginal revenue and is shown by the curve MR in Figure 6-1. The marginal revenue curve lies below the demand curve D because the extra revenue earned from selling another unit is less than the price.

To maximize its profit, the monopolist sells up to the point at which the marginal revenue MR earned from selling one more unit equals the marginal cost MC of producing one more unit. In Figure 6-1, the marginal cost curve is shown by MC. Because we have assumed, for simplicity, that marginal costs are constant, the MC curve is flat, although this does not need to be the case. To have marginal revenue equal marginal costs, the monopolist sells the quantity Q^M. To find the profit-maximizing price the monopolist charges, we trace up from quantity Q^M to point A on the demand curve and then over to the price axis. The price charged by the monopolist P^M is the price that allows the monopolist to earn the highest profit and is therefore the monopoly equilibrium.

Demand with Duopoly

Let us compare a monopoly with a duopoly, a market structure in which two firms are selling a product. We will not solve for the duopoly equilibrium but will just study how the introduction of a second firm affects the demand facing each of the firms. Knowing how demand is affected by the introduction of a second firm helps us understand how demand is determined when there are many firms, as there are in monopolistic competition.

In Figure 6-2, the industry faces the demand curve D. If there are two firms in the industry and they charge the same price, then the demand curve facing each firm is D/2. For example, if both firms charged the price P₁, then the industry demand is at point A, and each firm’s demand is at point B on curve D/2. The two firms share the market equally, each selling exactly one-half of the total market demand, Q₂ = Q₁/2.

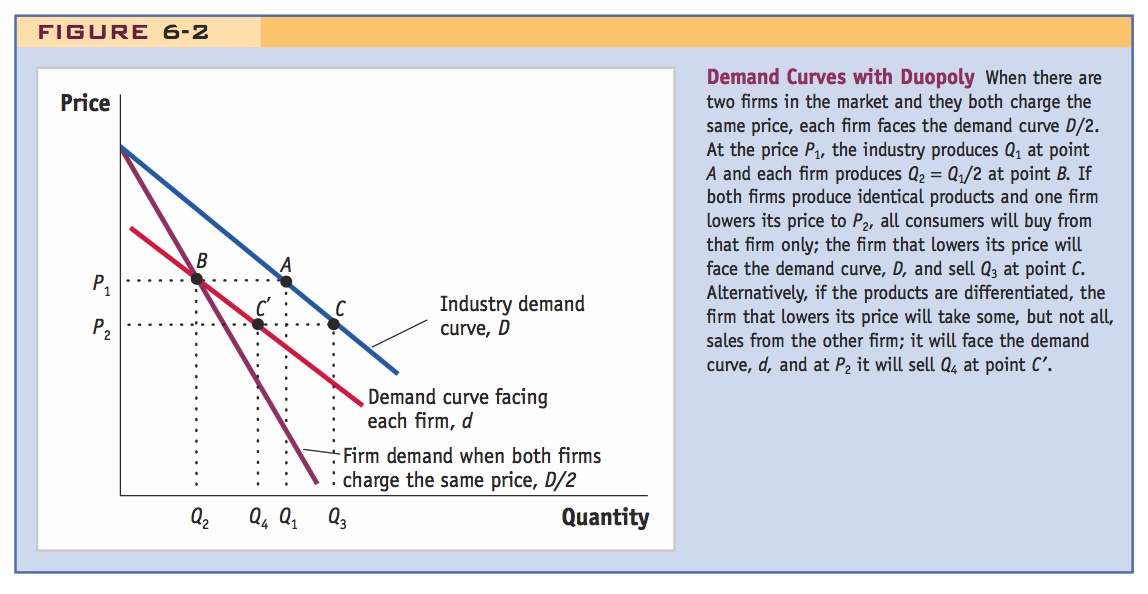
If one firm charges a price different from the other firm, however, the demand facing both firms changes. Suppose that one firm charges a lower price P₂, while the other firm keeps its price at P₁. If the firms are selling the same homogeneous product, then the firm charging the lower price would get all the demand (shown by point C), which is Q₃ at the price P₂. Now suppose that the products are not homogeneous but instead are differentiated. In that case, the firm with the lower price P₂ will capture more of the market than the firm with the higher price P₁, but will not capture the entire market. Because the products are not precisely the same (for instance, in our golf club example the higher-priced club is of better quality than the less expensive club), some consumers will still want to buy the other firm’s product even though its price is higher. The firm selling at the lower price P₂ now sells the quantity Q₄, for example, at point C′.

The demand curve d is the demand curve for the firm that lowered its price from P₁ to P₂, even though the other firm held its price at P₁. As we have illustrated, the demand curve d is flatter than the demand curve D/2. This means that each firm faces a more elastic demand curve than D/2: when only one firm lowers its price, it increases its quantity sold by more than when all firms lower their prices. Not only does the quantity demanded in the industry increase, but in addition, the firm that lowers its price takes away some of the quantity demanded from the other firm. In summary, the demand curve d facing each firm producing in a duopoly is more elastic than the demand curve D/2 each faces when the firms charge the same price.