APPENDIX 1 TO CHAPTER 18
The model developed in this chapter assumes that a depreciation of a country’s currency (a rise in q) will cause the trade balance to move toward surplus (a rise in TB). Is this assumption justified?
Let’s look at a simple example. Consider a hypothetical two-country world in which trade is initially balanced, so TB = 0 or EX = IM. The question of how the trade balance changes then simplifies to a question of whether the change in exports is greater or less than the change in imports. Let us consider a small percentage change in the real exchange rate, say, Δq/q = +1%, that is, a home real depreciation of 1%. Note that this is, approximately, a foreign real appreciation of 1%, since the foreign real exchange rate q* = 1/q is simply the inverse of the home real exchange rate, implying that Δq*/q* = −1%.
As we have argued, when home exports look cheaper to foreigners, the real value of home exports expressed in home units of output will unambiguously rise. This effect is described by the elasticity of home exports with respect to the home real exchange rate, denoted η, where
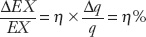
That is, if the home country experiences a 1% real depreciation, its real exports (measured in home units) rise by η%.
The same logic applies to the foreign country, with exports EX*, real exchange rate q* = 1/q, and elasticity η*, so that
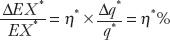
Now consider the trade link between the two countries. Foreign exports must equal home imports, measured in any consistent units. In home, real output units Home imports
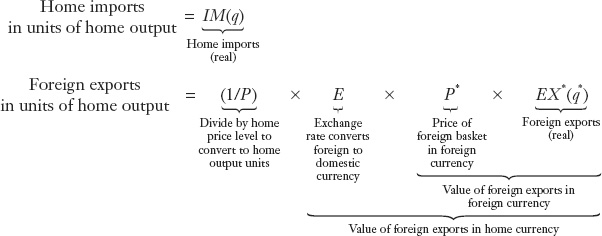
Equating these two terms, we find that IM(q) = (EP*/P) × EX*(q*). Thus,
IM(q) = q × EX*(q*)
302
This expression makes intuitive sense for the stylized two-country world that we are studying. It states that IM, the quantity of home imports (measured in home output units), must equal the quantity of foreign exports EX* (measured in foreign output units) multiplied by a factor q that converts units of foreign goods to units of home goods (since q is the relative price of foreign goods, that is home goods per unit of foreign goods).
For a small change, we may write the percentage change in the previous equation as follows. On the left is the percentage change in imports; on the right is the percentage change in q times EX*, which equals the percentage change in q plus the percentage change in EX*:
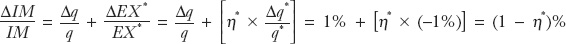
What is going on here? On the home import side, two effects come into play. Foreigners export a lower volume of their more expensive goods measured in foreign output units (a volume effect of −η*%), but those goods will cost more for home importers in terms of home output (a price effect of 1%). The price effect follows because the real exchange rate (the relative price of the foreign goods in terms of domestic goods) has increased (by 1%), and this makes every unit of imports cost more in real terms.
Starting from balanced trade with EX = IM, a 1% home real depreciation will cause EX to change by η% and IM to change by 1 − η*%. The trade balance (initially zero) will increase (to become positive) if and only if the former impact on EX exceeds the latter impact on IM. This occurs if and only if η > 1 − η*, or, equivalently,
η + η* > 1
The last expression is known as the Marshall–Lerner condition: it says that the trade balance will increase only after a real depreciation if the responsiveness of trade volumes to real exchange rate changes is sufficiently large (or sufficiently elastic) to ensure that the volume effects exceed the price effects.
303