APPENDIX 2 TO CHAPTER 18

How do the predictions of our model change when a country trades with multiple countries or regions? Can our theory be extended to this more realistic case? Can we make a sensible aggregation of trade flows, trade balances, and real exchange rates across, say, N different countries?

Suppose that for trade with any foreign country (say, country 1), the fractional change in home exports EX₁ and imports IM₁ given a small change in the real exchange rate q₁ is

The parameter ε > 0 is an elasticity. In this case, it is the elasticity of exports and imports with respect to the real exchange rate. When q rises by 1% (a real depreciation), exports rise by ε% and imports fall by ε%. (A more complicated analysis is needed when the import and export elasticities differ; see the first appendix.)

From these relationships, we find the following by rearranging:

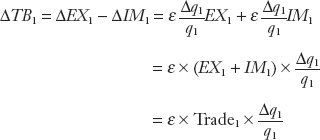
where Trade_i = [EX_i + IM_i] is the total trade of the home country with country i.

Adding up this last equation across all countries, the change in the home trade balance is given by ΔTB = ΔTB₁ + ΔTB₂ + … + ΔTB_N, which we can write as

We normalize by total trade, where Trade = Trade₁ + Trade₂ + … + Trade_N, to obtain

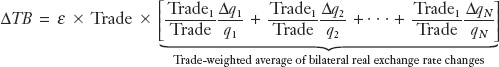
The expression in brackets might look familiar. In Chapter 2, we introduced the concept of a trade-weighted change in the nominal exchange rate—the change in the value of a currency against a basket of currencies, where the change in each country-pair’s nominal exchange rate was weighted by that particular country-pair’s share of trade volume. The preceding expression is similar, only with nominal exchange rates replaced by real exchange rates. The expression shows that (with some assumptions) our model can be extended to more realistic scenarios with many countries by using the change in a trade-weighted real exchange rate covering all trading partners.