3 How Pegs Break I: Inconsistent Fiscal Policies
Krugman's is of course the seminal paper, but the model developed here is much closer to Flood and Garber (JIE, 1984).
This section explains first-generation models.
1. The Basic Problem: Fiscal Dominance
Use a monetary model with flexible prices, exogenous income, and PPP. Assume the government runs persistent deficits that it forces the central bank to monetize: There is “fiscal dominance” because the central bank is not independent of the treasury. For simplicity, assume that domestic credit is initially constant, but then there is an unanticipated increase in its growth rate to ΔB/B = μ.
2. A Simple Model
Under flexible rates, the exchange rate would depreciate at the rate
a. The Myopic Case
Suppose first that people don’t anticipate the crisis. Initially R > 0 but as B increases R falls until it reaches zero and the peg is abandoned. After the collapse the price level and the exchange rate will increase at the rate μ; the increase in expected inflation will raise interest rates and lower money demand at the time of collapse. This requires a discontinuous jump in the price level and exchange rate when the collapse occurs. Notice that anyone holding the currency at the time of the collapse will take a capital loss.
b. The Forward-Looking Case
Assume perfect foresight. Speculators anticipate the loss in reserves and the ultimate collapse so they start selling the currency. When they dump all of their holdings at once, there is a speculative attack. But when will it occur? At the time of the collapse we switch immediately to the flexible rate equilibrium: from then on the exchange rate depreciates at the rate μ , so that at the time of the collapse interest rates increase, and money demand falls. Expecting the depreciation, speculators will sell the currency. Arbitrage dictates that they will sell it until the expected profits from doing so are driven to zero. This means that the path of the exchange rate must be continuous at the time of the collapse; otherwise there would be capital gains or losses from holding the currency. So the crisis occurs at the moment where the exchange rate that would hold conditional upon the crisis already having happened is equal to the pegged rate. The loss in reserves at the collapse depends critically upon how rapidly domestic credit is growing: the faster the growth in domestic credit, the sooner the collapse will occur and the larger will be the loss in reserves. Sometimes the government doesn’t have to pursue an unsustainable policy; it is enough for speculators to think that it might do so to precipitate a speculative crisis.
We begin with a so-called first-generation crisis model of inconsistent fiscal policies in a country with a fixed exchange rate, a model proposed by economist Paul Krugman.17 This kind of crisis model has been successfully applied to many historical cases, including a series of Latin American crises in the 1980s.
The Basic Problem: Fiscal Dominance
In this model, the level of output plays no role, so we assume output is fixed at some level Y. However, the price level P plays an important role, and we allow the price level to be flexible and determined by purchasing power parity (PPP), as in the chapter on the long-run monetary model. For now we keep all our earlier assumptions from this chapter.
Friedman says, "inflation is always and everywhere a monetary phenomenon." But Sargent retorts, "inflation is always and everywhere a FISCAL phenomenon."
In this model, the government is running a persistent deficit DEF because of insufficient tax revenue, and the government’s situation is so dire that it is unable to borrow from any creditor. It therefore turns to the central bank for financing. In this type of environment, economists speak of a situation of fiscal dominance in which the monetary authorities ultimately have no independence. The treasury hands over bonds in the amount DEF to the central bank, receives cash in the amount DEF in return, and uses the cash to fund the government deficit. As a result, domestic credit B increases by an amount ΔB = DEF every period. For simplicity, we assume that domestic credit B is growing at a constant positive rate, ΔB/B = μ. For example, if μ = 0.1, then domestic credit B is growing at 10% per period.
Given our previous graphical analysis of the central bank balance sheet, we can see that the fixed exchange rate is doomed. As in Figure 9-12, panel (a), every change in the level of domestic credit leads to an equal and opposite change in the level of reserves. This process can’t go on forever because reserves must eventually run out. At that point, the peg breaks and the central bank shifts from a fixed exchange rate regime to a floating regime, in which the money supply equals domestic credit, M = B. We note a key point:
Students may ask why the government persists in doing something so foolish. Answer by looking at data on the money supply for Mexico in the early 1980s, for example, to illustrate that it happens for extended periods. But admit that the exogeneity of the unsustainable policy is a legitimate criticism, and contributed to the development of second-generation models.
Once reserves run out, the money supply M, which was previously fixed, grows at the same rate as domestic credit, ΔM/M = ΔB/B = μ.
In fact, if you want to be adventurous, consider using a linear (in levels) money demand and follow Flood and Garber in solving the model algebraically. This does involve a simple differential equation, but it also allows you to introduce the idea of a shadow exchange rate, which makes the solution for the time of the collapse very clean.
The reason the peg breaks in this situation is simple. There is an inconsistency between the authorities’ commitment to a monetary policy of a fixed exchange rate and a fiscal policy of continuously monetizing deficits through an endless expansion of domestic credit. On the face of it, crisis results from elementary incompetence on the part of the authorities; to be more generous, we might say that the crisis happens because authorities are willing to let it happen because of overriding fiscal priorities.
A Simple Model
In many ways, this situation is familiar. We have already seen the implications of long-run money growth. In the chapter on exchange rates in the long run, we learned what happens in response to an unexpected increase in the rate of money supply growth: if prices can adjust flexibly, then, after the increase, the economy ends up with all nominal values growing at the rate μ, the rate of growth of domestic credit. There will be inflation as prices P rise at a rate μ, and depreciation as the exchange rate E rises at a rate μ.
380
The Myopic Case Figure 3-14 (p. 98) described a case in which the rate of growth of the money supply unexpectedly increased by a fixed amount. We apply the same analysis here and assume that investors are myopic and do not see the crisis coming. (To be more realistic, we relax this assumption in a moment, but the myopic case provides useful insights.)
Drawing on what we know, Figure 9-13 describes this kind of crisis scenario, assuming that prices are stable in the foreign country, that the foreign interest rate is i* = 5%, and that all variables change continuously through time. For simplicity, we start with M = P = E = 1, and at all times we assume the foreign price level is 1, P* = 1.
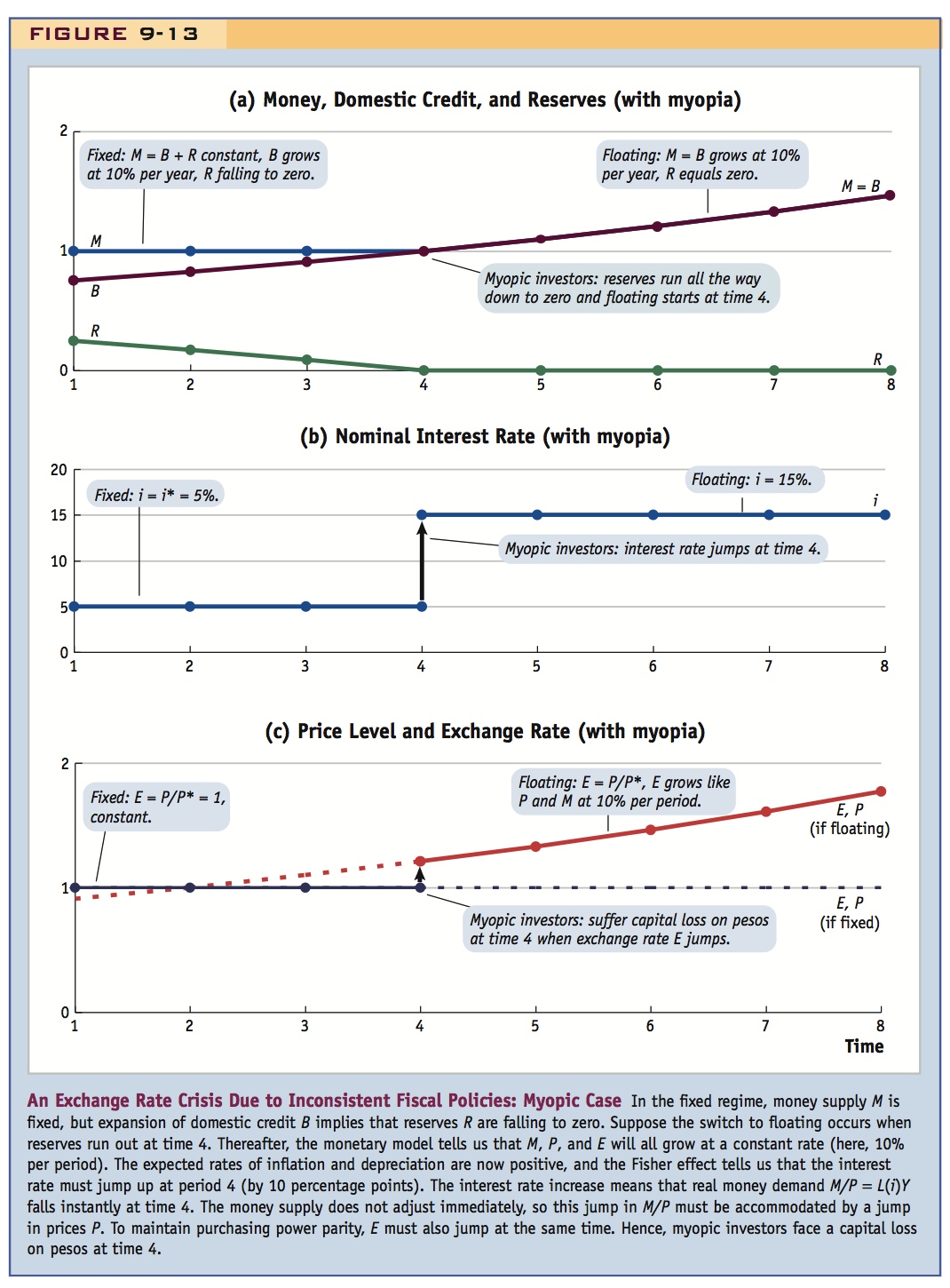
Starting at time 1, in the fixed regime, domestic credit is less than the money supply, B < M, and reserves are positive, R > 0. But because of the monetization of deficits, B is gradually rising, and, as a result, R is steadily falling. Eventually, reserves run out, and thereafter B = M and R = 0. We assume for now that the regime change occurs at time 4. In the fixed regime, up to that point, money supply M is fixed, but when floating starts, M grows at a rate μ as shown in panel (a).
This is what Flood & Garber call the "shadow exchange rate," conditional upon the collapse occur at t = 4.
Because prices are flexible, the monetary model of exchange rates in the long run tells us that P will be fixed until time 4 and then it will grow at a rate μ. Thus, inflation rises by an amount μ at time 4. The Fisher effect tells us that an increase in the home inflation rate causes a one-for-one increase in the home interest rate. So the home interest rate i must rise by an amount μ as we move from the fixed to the floating regime as shown in panel (b).
Make sure students understand the jump.
An increase in the home interest rate i at time 4 lowers the demand for real money balances, M/P = L(i)Y, because in the money demand function, L is a decreasing function of i. Thus, M/P “jumps” down as we change from fixed to floating. Because the money supply M does not change at time 4, the drop in M/P can be accommodated only by a jump in the flexible price level P at time 4. Because, by assumption, PPP holds continuously (and because P* = 1), then we can just compute E = P/P* = P. So the discontinuous rise in P also implies a discontinuous rise in E at time 4, and a depreciation of the home currency. Both E and P jump up and start to grow at rate μ at time 4, as shown in panel (c).
To sum up, in Figure 9-13, the exchange rate crisis occurs at time 4, but the exchange rate doesn’t drift continuously away from its previous fixed level. It jumps away discontinuously. The new floating path of the exchange rate rises at a growth rate μ, which is above the old fixed rate at time 4.
For example, if the money growth rate is 10% after the crisis, as assumed, then there is a 10 percentage point increase in the interest rate from 5% to 15%. Now suppose this reduces real money demand by 20%, from 1.00 to 0.80. Because the nominal money supply M equals 1 just before and just after the crisis, it does not jump at time 4. To get M/P to fall from 1.00 to 0.80, P must jump up, from 1.0 to (1/0.80) = 1.25, implying an instantaneous 25% increase in P. To maintain purchasing power parity, there must also be a 25% increase in the exchange rate E, to 1.25, followed by growth at 10%.
Emphasize this, since it is what will drive the attack once we drop the assumption of myopia.
One significant implication of the jump in nominal values is that anyone holding a peso that was worth 1 dollar will suddenly be left holding a peso that is worth only 1/1.25 = 0.80 dollar. Investors holding pesos at the moment of crisis will suffer a capital loss (in dollar terms) if this model accurately describes their behavior.
381
382
The Forward-Looking Case There is good reason to believe that investors will not be as shortsighted (myopic) as we have just assumed. It is usually well known when a government has a deficit that is being monetized, even if the authorities try to conceal the problem.
Let us move to the other extreme, forward-looking behavior, which for now we take to mean perfect foresight. Figure 9-14 explains how this scenario departs from the myopic version we just saw in Figure 9-13. Suppose peso holders see that domestic credit is rising and reserves are falling. Knowledgeable people will speculate that the fixed rate is going to break in the near future. They will expect pesos to suddenly lose their dollar value if they hold them until the bitter end at time 4 when reserves would run out under myopia. They will therefore decide to dump pesos sooner. But when? And how?
When investors sell all their holdings of a particular currency, it is known as a speculative attack. When such an attack occurs, the economy must immediately switch to the floating regime we have already studied, since once it has zero reserves, the money supply M will always equal domestic credit B—which has been and will be growing at the constant rate μ. At that same time, the nominal interest rate will also jump up, when the Fisher effect kicks in, and there will be a jump down in both money demand (as the interest rise hits) and in money supply (as the attack drains all remaining reserves).
This is when the shadow rate equals the peg.
In our example, the key lesson is that once an attack occurs, the economy completely switches over to the floating regime. Under myopia the switch occurred at time 4. But now, the switch happens well before time 4, and at the time of the attack the economy’s inflation, exchange rates, prices, and interest rates all jump to their new (and rising) paths. This leaves one question: When does the speculative attack occur? From Figure 9-14, the answer must be at time 2. In this case, the path of the price level P and the exchange rate E are continuous as we switch from fixed to floating. Only then can the switch occur without any expected dollar gains or losses on holding pesos.

This is a very clear explanation of the intuition for the arbitrage condition just expressed. But don't expect the students to grasp it immediately.
How does this pin down the attack at time 2? Suppose the attack were at any time later than 2, such as time 3. As we can see from the diagram, this requires a jump up in the exchange rate, a discontinuous depreciation. If peso holders wait to attack until time 3, they still suffer a capital loss because they have waited too long. What if the attack is before time 2, say, at time 1? An attack at time 1 implies a discontinuous appreciation of the peso. But if that happened, any individual peso holder would enjoy capital gains (in dollars) from holding on to pesos rather than exchanging them for reserves at the central bank at the prior fixed rate. They would rather wait, let everyone else attack, and pocket the gains. But if one person thinks like that, all do, and the attack cannot materialize.
The speculative attack model teaches an important lesson. One moment, a central bank may have a pile of reserves on hand, draining away fairly slowly, giving the illusion that there is no imminent danger. The next moment, the reserves are all gone. The model can therefore explain why fixed exchange rates sometimes witness a sudden collapse rather than a long, lingering death.
Mexico in the early 1980s is another dramatic example.
Peru adopts a fixed rate, but the government runs large budget deficits. The central bank monetizes the debt. Reserves plummet until Peru abandons the peg, after which the sol depreciates rapidly and hyperinflation starts.
3.Summary
First-generation models predict that unsustainable policies can cause currency crises. Even expectations that policies may be unsustainable can cause crises.
The Peruvian Crisis of 1986
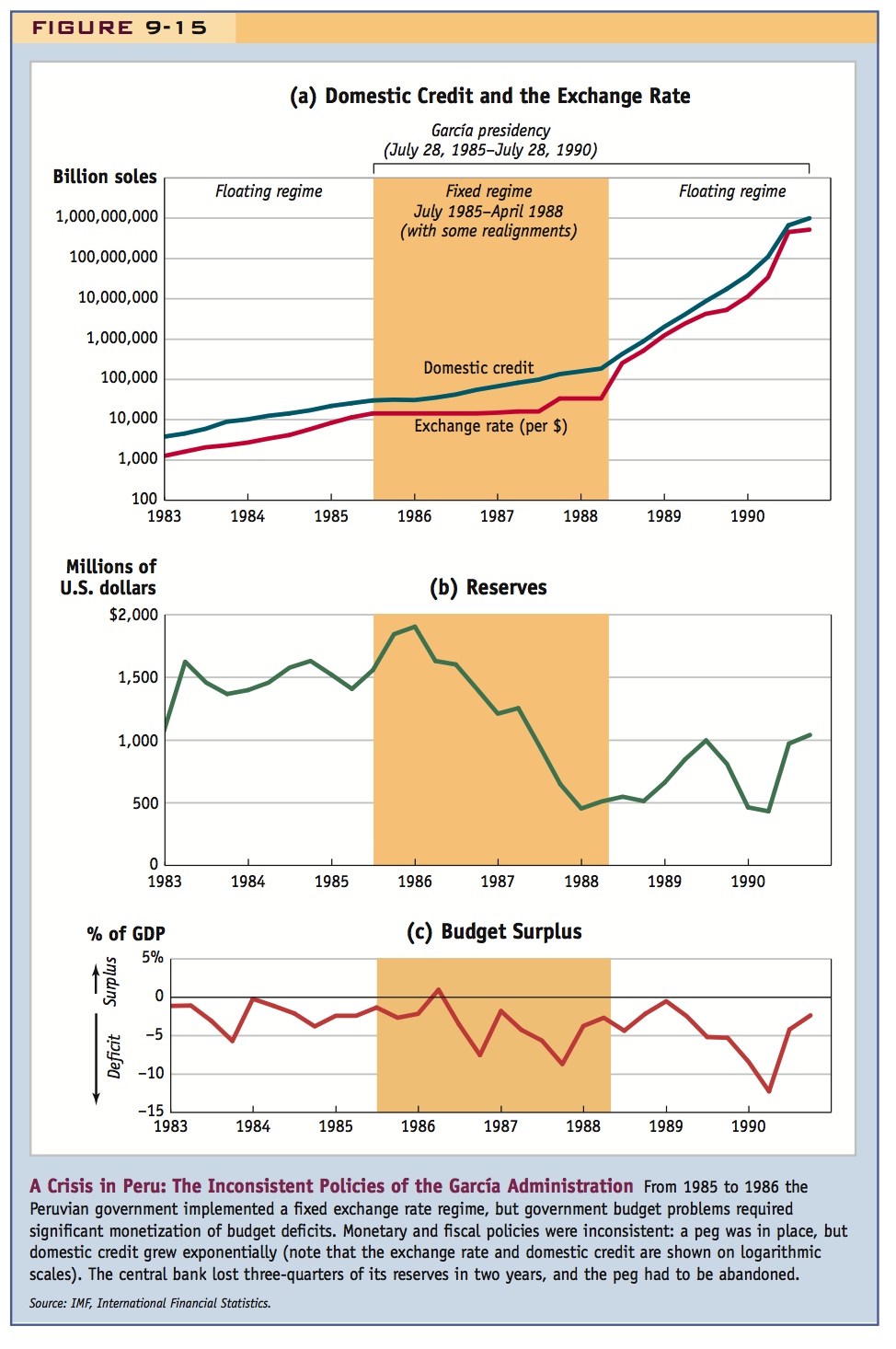
An example of a crisis driven by inconsistent fiscal policies and excessive expansion of domestic credit is provided by the events in Peru from 1985 to 1986, illustrated in Figure 9-15.
In the early 1980s, Peru’s political and economic conditions were highly unfavorable. The country had endured a period of social unrest and military rule in the 1970s, and the government had an enormous external debt burden. World commodity prices fell, exports and economic growth slowed, and government deficits grew. At the same time, world interest rates sharply increased.
383
384
385
The Peruvian government defaulted on its debt obligations and began negotiations with the IMF and other creditors. Denied fresh loans from world capital markets, and with low tax receipts that could not cover rising spending, government financing came to rely on money printing by the central bank—that is, the inflation tax. Domestic credit grew by 65% in 1982, 165% in 1983, and 93% in 1984—a rough doubling every year, on average. The dollar value of Peru’s currency, the sol, rapidly sank.
As economic conditions deteriorated further and political violence by guerilla groups intensified, President Alan García Pérez was elected to office in 1985. One important economic measure he instituted immediately was a fixed exchange rate. This stopped the depreciation and was intended to give Peru a firm nominal anchor. But, as we now know, its durability would depend on whether García’s administration could solve its fiscal problems and put an end to the monetization of government deficits.
Some fiscal reform was attempted, and the economy recovered slightly: the government budget improved at first. But the administration could not get the government budget out of the red for long. The deficit fell from 2% to 3% of GDP to near zero in early 1986, but by mid-1986 it was growing again, averaging over 5% and peaking at 8% to 9% of GDP in late 1986 and 1987. The printing presses of the central bank kept running, and domestic credit grew 84% in 1985, 77% in 1986, and 146% in 1987—roughly doubling every year.
Under a fixed exchange rate, something had to give. With domestic credit exploding, the central bank was continually selling reserves to defend the peg.18 Reserves fell from a peak of $2,000 million in early 1986 to $500 million in early 1988. The authorities gave up in April 1988 before the attack was complete and so avoided losing all their dollar reserves. The sol began to float and depreciation was rapid: the sol hit 250,000 sol/$ in September, 500,000 in November, and 1,200,000 by March 1989, and Peru was heading into a hyperinflation.19
The data closely match the predictions of the model. Under the peg, reserves drain as domestic credit grows, and the exchange rate is stable. Under the float, reserves are stable, and the exchange rate grows as domestic credit expands.
By the time García left office, Peru was in economic shambles. García’s popularity sank. The 1990 presidential election was won by a political newcomer, Alberto Fujimori, who would struggle with the problems created by his predecessor (and problems of his own). Yet, remarkably, in 2006 Alan García Pérez was elected president of Peru for a second time. Twenty years is a long time in politics.
Expectations and the Critical Level of Reserves What determines the critical level of reserves Rc at which the crisis occurs? In the speculative attack model, the size of the sudden reserve loss, and hence the timing of the crisis, depend critically on market expectations about the future growth rate of domestic credit. The reserves Rc lost at the moment of crisis will depend on how much money investors want to convert into reserves when they attack. This, in turn, depends on how much money demand shrinks as we move from fixed to floating, and that is driven by the change in the interest rate.
Let’s assume that each percentage point increase in the interest rate causes a ϕ% fall in real money balances.20 At the moment of attack, the interest rate rises by an amount Δi = μ, so the proportional fall in money demand is given by ϕ times that change. Thus, the change in money demand is given by −ΔM/M = ϕ × μ.
386
But we also know that the change in the money supply at the moment of attack −ΔM has to correspond exactly to the size of the reserve drain at the moment of attack, which equals the critical level of reserves Rc that are lost at that instant. Thus,
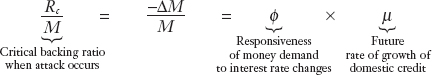
This expression tells us the ratio of the critical level of reserves Rc to the money supply M. It depends on the sensitivity of money demand to the interest rate and on the expected future rate of growth of domestic credit μ (remember, investors are forward-looking).
To illustrate, and continue our previous example, if the growth rate of domestic credit is expected to be μ = 10%, and if ϕ = 1.5, then the fall in money demand and money supply at the moment of attack is 10% times 1.5, or 15%. Thus, when reserves have drained so far that the backing ratio falls to the critical level Rc = 15%, the peg will break. But if μ rises to 20%, the critical level Rc would be twice as large, 30%.
We can now see that if people expect a fiscal problem to worsen (expect the deficit to increase, and thus domestic credit to grow faster to finance it), then reserves drain away faster, and the crisis hits sooner, at a higher critical level of reserves Rc. Thus, an increase in the expected rate of deficit monetization shortens the length of time that the peg will survive.
This result emphasizes the importance of market beliefs. Suppose a country has reserves well above the critical level. There is no imminent crisis. Then market beliefs change, perhaps because news or rumors emerge about a budget problem. Investors now expect a higher growth rate of domestic credit. Suppose that, as a result of this change in expectations, the critical level of reserves rises so much as to equal the current level of reserves. With the change in expectations, the time for a speculative attack is now. A crisis will happen immediately, even though there has been no change in the economic situation as of today!
In fact, as noted below, the crisis might occur even if there is no budget problem. Compare Mexico in the 1990s with Mexico in the 1980s, or perhaps the ERRM in the 1990s. There could simply be an irrational, self-fulfilling run against the currency.
Summary
The first-generation crisis model tells us that inconsistent fiscal policies can destroy a fixed exchange rate. Yet it is not actual fiscal policy that matters, but beliefs and expectations about future fiscal policy. Because beliefs about future deficits may or may not be justified, the model opens up the possibility that countries will be punished for crimes they do not intend to commit.
For example, some economists have argued that expected future deficits were a factor in the Asian currency crisis of 1997: the countries were affected by “crony capitalism” and the banking sectors were insolvent because of bad loans to insiders. Once the scale of these problems became known, investors believed that the monetary authorities would bail out the banks. Fears of a rapid future expansion of domestic credit thus undermined the pegs.21
387