Chapter 15. Question 15

Question 15

true

You must read each slide, and complete any questions on the slide, in sequence.

Use the two different distributions of income in the table below to answer the questions that follow.

Quintile	A	B
Poorest	10.5	2.5
Second	13.2	6.8
Middle	21.6	13.9
Fourth	26.4	24.2
Richest	28.3	52.6

A. Answer the following questions about how to graph these Lorenz Curves:

A1. On the graph for the Lorenz Curve, the vertical axis is and the values are , and the horizontal axis is the and the values are .

Incorrect! The vertical axis represents percentage of income, and the horizontal axis represents the percentage of households. Both are cumulative, and include the current quintile as well as lower quintiles.

Correct! The vertical axis represents percentage of income, and the horizontal axis represents the percentage of households. Both are cumulative, and include the current quintile as well as lower quintiles.

A2. Fill in the table for cumulative income distribution:

Quintile	A	Cumulative	B	Cumulative
Poorest	10.5		2.5
Second	13.2		6.8
Middle	21.6		13.9
Fourth	26.4		24.2
Richest	28.3		52.6

Incorrect! For the lowest quintile, the cumulative value is the value for that quintile. For every other quintile, the cumulative value is calculated by adding the previous cumulative value and the quintile’s non-cumulative value. For example, Country A’s second quintile cumulative value includes the first quintile as well as the second quintile’s (non-cumulative) value. 10.5 + 13.2 = 23.7. This is done for all cells. Since there is no previous value to add for the poorest quintile, the cumulative and non-cumulative values are the same.

Correct! For the lowest quintile, the cumulative value is the value for that quintile. For every other quintile, the cumulative value is calculated by adding the previous cumulative value and the quintile’s non-cumulative value. For example, Country A’s second quintile cumulative value includes the first quintile as well as the second quintile’s (non-cumulative) value. 10.5 + 13.2 = 23.7. This is done for all cells. Since there is no previous value to add for the poorest quintile, the cumulative and non-cumulative values are the same.

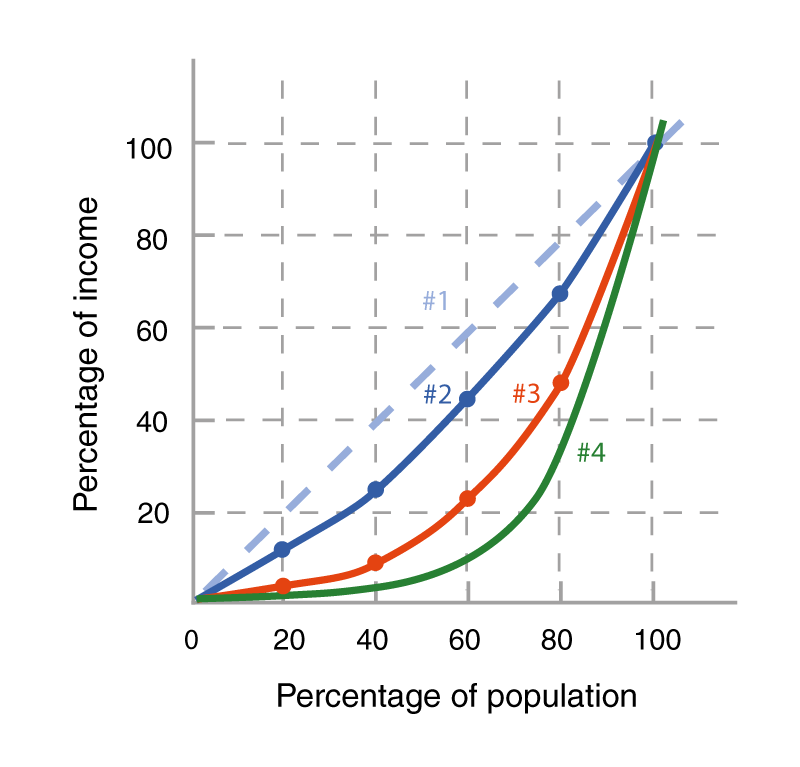
A3. On the graph below, Country A’s Lorenz curve is depicted and Country B’s Lorenz curve is depicted by .

Incorrect! Lines #2 and #3 correspond to Country A and Country B’s cumulative income distributions point by point. For example, A’s first two points, in x-y format, would be (20, 10.5) and (40, 23.7). Line #4 represents an income distribution that is more unequal than either of the provided countries.

Correct! Lines #2 and #3 correspond to Country A and Country B’s cumulative income distributions point by point. For example, A’s first two points, in x-y format, would be (20, 10.5) and (40, 23.7). Line #4 represents an income distribution that is more unequal than either of the provided countries.

B. Which curve has a more equal distribution?

Incorrect! A’s Lorenz curve is much closer to the equal distribution line than is B’s Lorenz curve. In addition, in Country B each quintile except the richest has a greater share of income in Country A.

Correct! A’s Lorenz curve is much closer to the equal distribution line than is B’s Lorenz curve. In addition, in Country B each quintile except the richest has a greater share of income in Country A.

C. Are these distributions more or less equal than that for the United States today (2014 data presented on p. 400 of the text, Table 2)?

These distributions are both more equal than that for the United States today.

These distributions are both less equal than that for the United States today.

The distribution for the United States today is between the two distributions.

Incorrect! The quintiles for 2014 are, from poorest to richest: 3.1, 8.2, 14.3, 23.2, and 51.2, resulting in cumulative numbers of 3.1, 11.3, 25.6, 48.8, and 100. These cumulative numbers are in between the corresponding numbers for Country A and Country B. Plotting them on an additional Lorenz curve would yield a curve that was between the two curves.

Correct! The quintiles for 2014 are, from poorest to richest: 3.1, 8.2, 14.3, 23.2, and 51.2, resulting in cumulative numbers of 3.1, 11.3, 25.6, 48.8, and 100. These cumulative numbers are in between the corresponding numbers for Country A and Country B. Plotting them on an additional Lorenz curve would yield a curve that was between the two curves.