Chapter 25 Branched Tutorial: Hardy-Weinberg

Problem Statement

Assume that the phenotypes of lady beetles shown in the figure at the right are encoded by the following genotypes:

Phenotype Genotype
All black BB
Some black spots Bb
No black spots bb

For the lady beetles shown in the figure, calculate the frequencies of the genotypes and frequencies of the alleles. Determine if the population is in Hardy-Weinberg equilibrium by using a chi-square test. Be sure to round your answer to 2 decimal places.

Question

Genotypes:
Frequency of BB
Frequency of Bb
Frequency of bb
Alleles:
Frequency of B
Frequency of b

Use a chi-square test to determine if the lady beetles shown are in Hardy Weinberg equilibrium.

Chi-square value =

2
Great job!
At least one of your answers is incorrect. Be sure that you are rounding your answer to 2 decimal places. Try again or click "Work Problem Step by Step" to go through the tutorial steps.
Incorrect.
false
If you think you know how to solve the problem, enter your answers above and click "Submit Answers." Your answers will be checked and, if there are any mistakes, you'll be given one chance to revise them. If there are still mistakes after your second attempt, you'll be guided through the process of solving the problem. If you want to go straight to that guided process, click "Work Problem Step-By-Step."

2
Great job!
At least one of your answers is incorrect. Be sure that you are rounding your answer to 2 decimal places. Try again or click "Work Problem Step by Step" to go through the tutorial steps.
Incorrect.
false

Problem Strategy

Question

Determine the best approach to solve this problem by ordering the following steps:

  1. Determine the allele frequencies in the population.
  2. Determine the genotypic frequencies in the population.
  3. Interpret the chi-square value.
  4. Identify the question that is being asked and focus on key pieces of information.
  5. Conduct a chi-square test.
  6. Determine the expected number of individuals in each class if the population is in Hardy-Weinberg equilibrium.

Which of the following is the correct order of steps that should be used to solve this problem?

A.
B.
C.
D.
2
Correct, this is the best approach to solving this problem.
Incorrect.

Instant TA

Think about the steps listed and how they logically flow from one to another, from general, information-gathering steps to more specific steps related directly to the question.

Step 1: Understanding the Problem

Question

1. How many individuals are in this population?

A.
B.
C.
2
Correct.
Incorrect.

Instant TA

You will need to count the total number of lady beetles in this population.

Step 2: Calculating Genotypic Frequencies

Question

1. Indicate the total number of black lady beetles in the figure.

Number of black lady beetles =

2
Correct.
Try again. Be sure to look at the number of individuals displaying the trait.
Incorrect.

Instant TA

Use the displayed figure to count the total number of lady beetles that are all black.

Step 3: Calculating Allele Frequencies

Question

1. Indicate the correct values for nBB, nBb, and N in the following equation:

          p = f(B) = (2nBB + nBb)/2N

p will represent the frequency of the B allele. nBB and nBb represent the number of individuals of each genotype. N represents the total number of individuals in the population.

 

nBB =
nBb =
N =

2
Correct.
Try again. Be sure to look at the number of individuals for each genotype.
Incorrect.

Instant TA

Identify the number of individuals with genotype BB and genotype Bb.

More About This Equation

In this equation, the frequency of the B allele is being represented by p. In order to calculate p, the total number of B alleles and total number of alleles in the population are needed. 2nBB represents the number of B alleles in the homozygotes (remember, for each homozygous individual there are two alleles—this is why we multiply the number of individuals with genotype BB by two). nBb represents the total number of B alleles in the heterozygotes (since each individual only has one B allele, there is no need to multiply by any factor). 2N represents the total number of alleles in the population (each individual has two alleles at each locus).

Step 4: Calculating Expected Genotypic Frequencies for a Population in Hardy-Weinberg Equilibrium

Question

1. In the Hardy-Weinberg equilibrium equation, which expression represents the expected frequency of the BB genotype?

p2 + 2pq + q2 = 1

A.
B.
C.
2
Correct.
Incorrect.

Instant TA

We are letting p represent the frequency of the B allele. The BB genotype has 2 B alleles.

Step 5: Conducting a Chi-Square Test

Question

1. A table can help organize your calculations for the chi-square test. In the table, the letters A-E represent column headings. To provide the best approach to arriving at the final chi-square value, use the dropdown menus below to match the correct column heading title with the correct letter.

A B C D E
BB (all black)
Bb (some black spots)
bb (no black spots)

(Observed - Expected)2/Expected
Expected
Observed
Observed - Expected
(Observed - Expected)2

2
Correct.
Try again. At least one of your answers in incorrect.
Incorrect.

Instant TA

The column indicated by “A” should include the information that is provided to you. In the remaining columns, you will work in a stepwise manner to obtain the values that will be used for the chi-square calculation.

Show Chi-Square Equation

χ2 = Σ(observed - expected)2 / expected

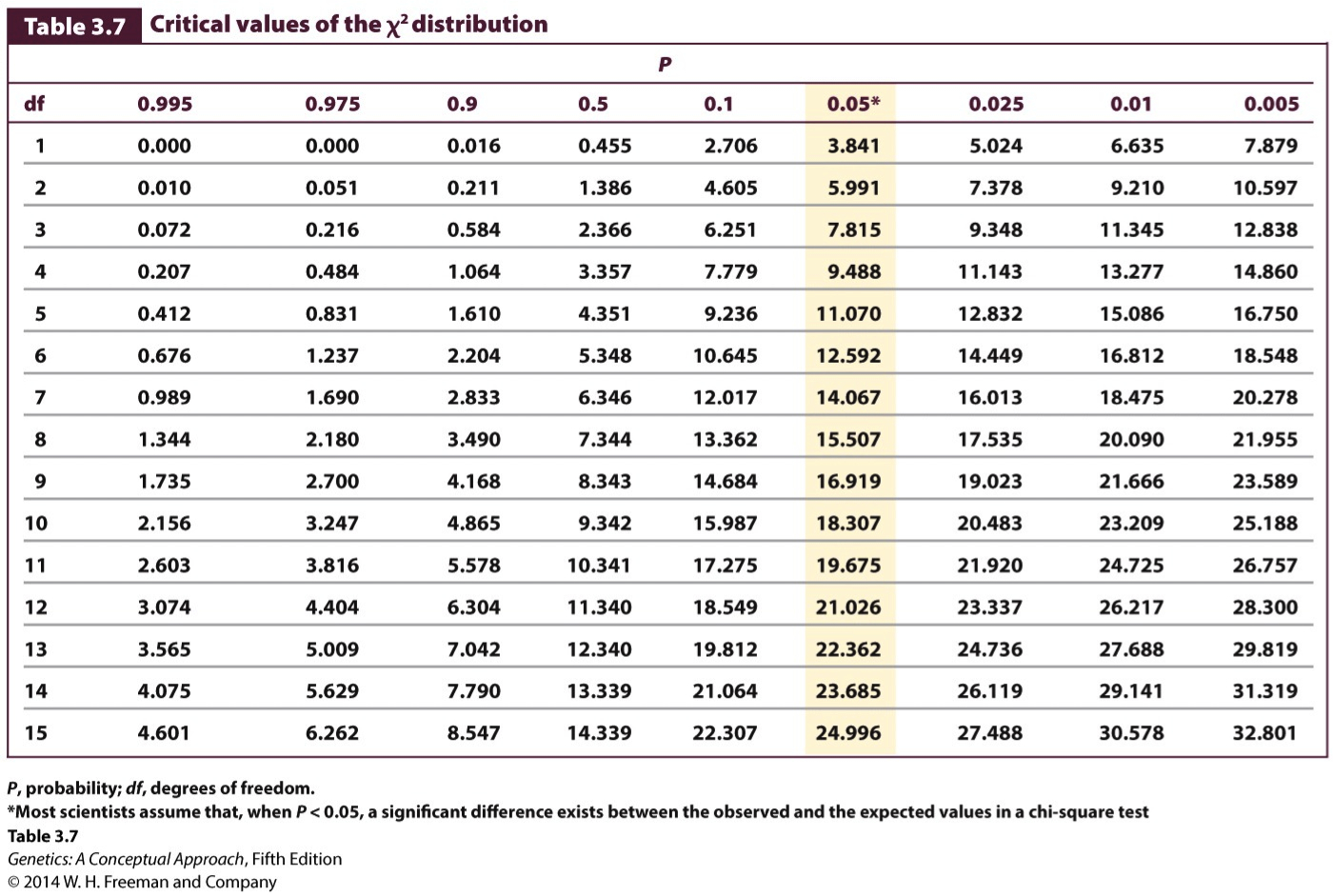
Step 6: Interpreting the Chi-Square Value

Question

1. How many degrees of freedom should be used to determine the significance of the chi-square value?

A.
B.
C.
2
Correct.
Incorrect.

Instant TA

Generally, the degrees of freedom for a chi-square test of Hardy–Weinberg equilibrium equal the number of expected genotypic classes minus the number of associated alleles.

Notes: