APPENDIX 2 Map Projections
APPENDIX 2 Map Projections
Maps are flat, two-dimensional representations of Earth’s surface. A globe is a three-dimensional replica of the planet. World maps cannot portray the globe’s curved surface without distorting the shapes and sizes of continents and ocean basins. To illustrate this distortion, imagine you have a soccer ball with Earth printed on it. A traditional soccer ball has 32 patches that are stitched together to make a sphere. It is impossible to lay these patches out on a flat piece of paper without causing gaps between the patches in the oceans or continents, as shown in Figure A.1.

A sphere converted to a flat map. When a sphere is forced onto flat paper, gaps result.
Only a globe can keep the sizes and shapes of Earth’s features accurate. But a globe has many limitations:
Only half a globe can be viewed at one time.
The edges of the visible half are distorted.
Globes are always at a small scale, and it is impossible to show details clearly.
Globes are more expensive to make than maps and less versatile in terms of creating new themes, such as vegetation cover or earthquake patterns.
Globes do not fit well into pockets or drawers.
Because of the limitations of globes, flat world maps will always be needed. But the problem of how to handle the gaps that result when the globe is transferred to a flat surface remains. Cartographers address that problem by using map projections.
Types of Map Projections
Cartographers use map projections to transfer the global surface onto a flat map surface. This process is called “projecting” because, before computers, cartographers used a light to project the outline of a wire globe onto a flat piece of paper, then traced the shadows onto the paper. The type of projection that resulted depended on how the paper was positioned in relation to the light. In all, there are three basic kinds of projections: cylindrical, conic, and azimuthal (Figure A.2).

Map projections. Each projection type has a different application and use. The red line or dot represents the tangent where the map touches the globe. Map distortion increases with distance from the tangent.
Page A-3
Equal-Area and Conformal Maps
There are two ways to address the gaps that result from stretching the global surface onto a flat piece of paper: preserve areas and sacrifice shapes, or preserve shapes and sacrifice areas. Equal-area projections preserve areas at the expense of shapes (Figure A.3).
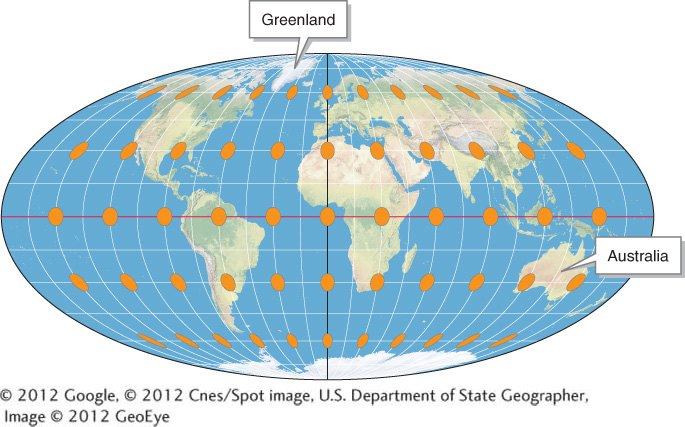
Mollweide equal-area projection. The orange circular areas are all approximately the same size and cover roughly the same geographic area no matter where on the map they are placed. This equalization of area is accomplished by compressing and distorting regions near the poles. Note that the orange areas at high latitudes become distorted ellipses compared with those at low latitudes. This equal-area map shows the true areas of Earth’s surface: note, for example, that Australia is over three times larger than Greenland. The Mollweide projection is used throughout Living Physical Geography.
(© 2012 Google, © 2012 Cnes/Spot image, U.S. Department of State Geographer, Image © 2012 GeoEye)
A conformal projection preserves the shapes of continents at the expense of areas. Areas in a conformal map are distorted in different portions of the map. In the example shown in Figure A.4, high latitudes are stretched and expanded to preserve the true shapes of continents.
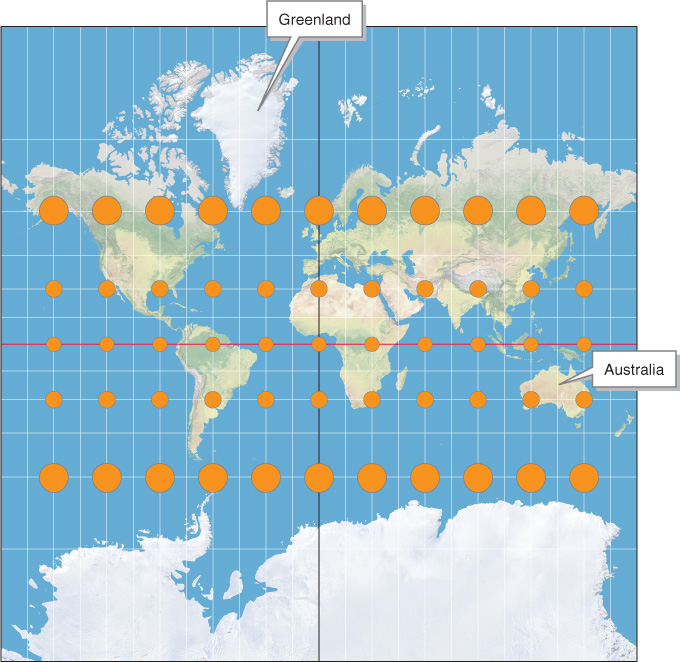
Mercator conformal projection. Even though they are of different sizes, all the orange areas on this map are perfect circles and cover the same amount of Earth’s surface. Compared with those in the tropics, the circles at high latitudes are larger because those areas have been stretched. Notice that Greenland appears far larger than Australia in this projection. Antarctica’s size is also greatly exaggerated. See the Mollweide projection in Figure A.3 to compare the relative areas of these landmasses.
Only globes are both conformal and equal-area representations of Earth. Unlike a globe, no single world map projection can show both shapes and areas accurately.
Page A-4



