Problems
(Solutions to problems marked * appear at the back of this book. Problems adapted to use calculus are available online at www.macmillanhighered.com/
Many textbooks are now available in two versions, a high-
priced “domestic” version and a low- priced “international” version. Each version generally contains exactly the same text, but slightly altered homework problems. Why would a textbook publisher go to the trouble to produce two versions of the same text?
Discuss whether the publisher’s strategy would be more effective if it made the alterations secret, or if it announced them boldly.
The production of international versions of textbooks was concurrent with the explosion of the Internet. Explain why this is likely to be more than just a coincidence.
Consider the demand for schnitzel in the following diagram. Suppose that there is a single seller of schnitzel, who acts as a single-
price monopolist. 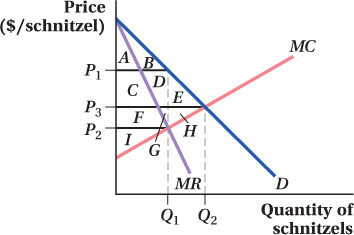
Indicate the profit-
maximizing price and quantity. The profit-
maximizing price is P1 and quantity Q1. List the areas of consumer and producer surplus.
The consumer surplus is A and B. The producer surplus is C, D, F, G, and I.
Suppose the seller begins perfectly price-
discriminating. How many schnitzels will she sell? The seller will sell Q2 schnitzels.
What happens to areas A and B when the seller begins perfectly price-
discriminating? Once the seller begins to perfectly price-
discriminate, areas A and B, the original consumer surplus, becomes part of the new producer surplus. What happens to areas E and H when the seller begins perfectly price-
discriminating? Areas E and H are no longer the deadweight loss, but become part of the producer surplus.
416
-
There are seven consumers, each of whom is hungry for exactly one Butterfinger. The consumers’ maximum willingness to pay is given in the table below:
Consumer (age, gender) Maximum Willingness to Pay Marge (34, female) $2 Homer (38, male) 4 Lisa (6, female) 5 Maggie (2, female) 6 Ned (46, male) 1 Krusty (55, male) 3 Bart (9, male) 7 Given that each consumer wants one and only one Butterfinger, draw the demand curve for Butterfingers.
If Butterfingers are priced at $7, only one will be sold. Who buys that Butterfinger? Label the point at $7 on the demand curve with the name of that buyer.
If Butterfingers are priced at $6, a second buyer will be priced into the market. Who is that buyer? Label the point at $6 on the demand curve with the name of that buyer.
Continue to label each point on the demand curve with the name of the buyer represented by that point.
Suppose that you are a monopoly seller of Butterfingers, which you can produce at a constant marginal and average total cost of $2. Suppose you charge every customer the same price for Butterfingers. What price should you set to maximize your profit? How many Butterfingers will you sell? Calculate your profit. Calculate the consumer surplus received by the buyers. Calculate the deadweight loss.
Suppose that every customer that comes into your Butterfinger store has their maximum willingness to pay displayed in neon on their foreheads. You decide to use this information to increase your profit by practicing first-
degree price discrimination. How many Butterfingers will you sell? Calculate your profit. Calculate the consumer surplus received by the buyers. Calculate the deadweight loss. Where does the consumer surplus go when you begin price-
discriminating? What happens to the deadweight loss?
Most colleges and universities publish a single tuition figure, often right on their Web site. Yet, it’s claimed that colleges and universities are masters of first-
degree price discrimination. Explain how, in the real world, colleges and universities charge different students different prices for access to the same good.
First-
degree price discrimination requires information about individual customers’ demands. Where do colleges and universities get the information they need to estimate each prospective student’s willingness to pay? One requirement to implement first-
degree price discrimination is the ability to prevent resale. Explain why colleges and universities don’t have to worry about that. Are there other businesses you can think of where resale simply isn’t possible?
Consider the problem faced by the Butterfinger seller in Problem 3.
Assume that the seller is able to prevent resale between customers. In the real world, why is the seller still unlikely to be able to perfectly price-
discriminate? Because of the reason you just indicated, the Butterfinger seller decides to segment her customers into two groups, each of which will be charged a different price. In order to maximize profit, should the seller sort by gender or by age?
Based on your answer to (b), determine who is in each group, and indicate (1) the price the seller should set for each group, (2) the total profit received by the seller, (3) total consumer surplus, and (4) the deadweight loss.
Is this pricing strategy (segmenting) more profitable to the seller than perfectly price-
discriminating? Is this pricing strategy more profitable than charging every consumer the same price? What happens to consumer surplus and deadweight loss when a single-
price monopolist begins segmenting in this way?
417
Promoters of a major college basketball tournament estimate that the demand for tickets on the part of adults is given by Qad = 5,000 – 10P, and that the demand for tickets on the part of students is given by Qst = 10,000 – 100P. The promoters wish to segment the market and charge adults and students different prices. They estimate that the marginal and average total cost of seating an additional spectator is constant at $10.
For each segment (adults and students), find the inverse demand and marginal revenue functions.
The inverse demand for adults is
P = 500 – 0.1Q
Hence, the marginal revenue is
MR = 500 – 0.2Q
The inverse demand for students is
P = 100 – 0.01Q
Hence, the marginal revenue is
MR = 100 – 0.02Q
Equate marginal revenue and marginal cost. Determine the profit-
maximizing quantity for each segment. The profit-
maximizing quantity for adults is MR = MC
500 – 0.2Q = 10
Q = 2,450
The profit-
maximizing quantity for students is 100 – 0.02Q = 10
Q = 4,500
Plug the quantities you found in (b) into the respective inverse demand curves to find the profit-
maximizing price for each segment. Who pays more, adults or students? The profit-
maximizing price for adults is P*ad = 500 – 0.1Q*ad = 500 – (0.1 × 2,450)
= $255
The profit-
maximizing price for students is P*st = 100 – 0.10Q*st = 100 – (0.01 × 4,500)
= $55
Adults pay more.
Determine the profit generated by each segment, and add them together to find the promoter’s total profit.
The profit from adults is
TR – TC = ($255 × 2,450) – ($10 × 2,450)
= $600,250
The profit from students is
TR – TC = ($55 × 4,500) – ($10 × 4,500)
= $202,500
Hence, the total profit is $802,750.
How would your answers change if the arena where the event was to take place had only 5,000 seats?
Given that the capacity is 5,000, continue to sell 2,450 tickets to adults at $255, which maximizes profit in that segment. Sell the remaining 2,550 tickets for as much as the student segment will bear, $74.50. So, students should pay $74.50 = 100 – (0.01 × 2,550). Profit in the student segment would be ($74.50 × 2,550) – ($10 × 2,550) = $164,475. The total profit in this case would be $164,475 + $600,250 = $764,725.
You are the owner of a nail salon. Your female customer’s price elasticity of demand for manicures is –2.5; your male customer’s price elasticity of demand for manicures is –1.2. The marginal cost of manicuring a customer’s nails is $12.
If you segment the market by gender, what price should you charge women? What price should you charge men?
Explain intuitively why you should charge each group a different price.
Movie theaters often charge substantially less for afternoon showings than for evening showings. Explain how theaters use time of day to segment their customers into low-
elasticity and high- elasticity groups. Owners of a Florida restaurant estimate that the elasticity of demand for meals is –1.5 for senior citizens and –1.33 for everyone else.
The restaurant is considering offering a senior citizen discount. Use Lerner indices to determine how big (in percentage terms) that discount should be. (Hint: Determine the ratio of the senior citizens’ price to the price for everyone else.)
Suppose that the restaurant owners discover that seniors tend to demand more attention from their waiters and send back more food as unsatisfactory, to the extent that the marginal cost of serving a senior is twice as high as serving an adult. Accounting for these costs, how large should the senior citizen discount be? (Hint: Refer back to the example in the text, but don’t cancel out marginal costs!)
Were your results in part (b) surprising? Explain them, intuitively.
A local golf course’s hired-
gun econometrician has determined that there are two types of golfers, frequent and infrequent. Frequent golfers’ annual demand for rounds of golf is given by Qf = 24 – 0.3P, where P is the price of a round of golf. In contrast, infrequent golfers’ annual demand for rounds of golf is given by Qi = 10 – 0.1P. The marginal and average total cost of providing a round of golf is $20. If the golf course could tell a frequent golfer from an infrequent golfer, what price would it charge each type? How many times would each type golf? How much profit would the golf course generate?
The greens manager has difficulty telling frequent from infrequent golfers, so she decides to use second-
degree price discrimination (quantity discounts) to make different types of golfers self- select into the most profitable pricing scheme. The course sets a price for individual rounds of golf, but also offers a quantity discount for members willing to buy a rather large quantity of rounds in advance. The course’s owners hope that frequent golfers will self- select into the discounted plan, and that infrequent golfers will choose to buy individual rounds. What price should the golf course set for individual rounds of golf? Why?
If the course wishes to maximize profit, what price and minimum quantity should it establish for the discounted plan?
Which plan will generate the greatest consumer surplus for frequent golfers, the individual-
round plan or the discount plan? Illustrate your answer by showing and measuring the areas of surplus on frequent golfers’ inverse demand curves. Which plan will generate the greatest consumer surplus for infrequent golfers, the individual-
round plan or the discount plan? Illustrate your answer by showing the areas of surplus on infrequent golfers’ inverse demand curves. Based on your answers to (d) and (e), will the plan be successful in making golfers self-
select into the most profitable plan for the golf course? Suppose that each type of golfer came to the course with the word “frequent” or “infrequent” tattooed on his or her forehead. Is this information of any value to the golf course owner? (In other words, can the owner earn any more profits by segmenting than it did with its quantity discount plan?)
418
-
Carolina Atlantic sells specialty paper to commercial clients. Some clients are intensive users who are price-
sensitive; their demands are given by P = 8 – 0.1Q, where Q is the number of reams of paper desired per week. Other clients are less- intensive users of paper and have inverse demands given by P = 10 – 0.2Q. Let MC = 0. Carolina Atlantic attempts to separate more-
intensive and less- intensive buyers by implementing a quantity discount plan. What price should Carolina Atlantic set for each group? How should the quantity discount plan be structured? Show that the quantity discount plan you outlined in (a) is not incentive-
compatible. Suppose, instead, that intensive users had inverse demands given by P = 8 – (1/15)Q. Determine the structure of the quantity discount, and show that the plan is incentive-
compatible. Why did the quantity discount plan outlined in (b) fail, while the quantity discount plan outlined in (c) succeeded?
Rockway & Daughters Piano Co. wishes to sell a piano to everyone. But some consumers are budget-
conscious, and others are not, and unfortunately, Rockway cannot tell which is which. So, Rockway produces a premium line of pianos that it markets under the Rockway name, and a similar line of pianos that it markets under the Dundee name. While the cost of producing these pianos is quite similar, all consumers agree that Rockway pianos are of higher quality than Dundee pianos, and would be willing to pay more for a Rockway. Budget- conscious consumers feel that Dundee pianos are worth $6,000, and Rockways are worth $8,000. Performance artists believe that Dundee pianos are worth $7,000 and Rockways are worth $12,000. Suppose Rockway & Daughters prices its Dundee pianos at $5,000 and its Rockway pianos at $10,500. Are these prices incentive compatible—
that is, will more price- conscious consumers purchase the Dundee line, while more performance- oriented players choose the Rockway? Explain. The price-
conscious consumers will buy the Dundee pianos because their valuation exceeds the price of lower- quality pianos; the price of Rockway pianos exceeds the valuation of the higher- quality pianos by these customers. Thus, for budget- conscious customers, incentive compatibility is sustained. However, the net gain for performance- oriented consumers from buying Dundee pianos is $2,000, whereas for Rockway pianos it is $1,500. Therefore, the incentive compatibility condition is violated, as performance- oriented consumers would rather choose the Dundee pianos. Consumer Valuations for Dundee and Rockway Dundee (Budget Line) Rockway (Premium Line) Budget Consumer $6,000 $8,000 Luxury Consumer $7,000 $12,000 Consumer Surplus at $5,000 for Dundee and $10,500 for Rockway
Dundee (Budget Line) Rockway (Premium Line) Budget Consumer $1,000 −$2,500 Luxury Consumer $2,000 $1,500 How much must Rockway & Daughters reduce the price of its Rockway line in order to achieve incentive compatibility?
The price of Rockway pianos should be reduced by at least $500, but by less than $3,500.
Suppose instead that Rockway & Daughters tries to achieve incentive compatibility by raising the price of its Dundee line. Can it do so? And if so, how?
Yes, incentive compatibility can be achieved by raising the price of Dundee pianos from $5,000 to at least $5,501 (but not higher than $6,000). Then, budget-
conscious consumers will still buy Dundee pianos and performance- oriented professionals will choose the Rockway pianos. If you ran Rockway & Daughters Piano Co., which method would you use to achieve incentive compatibility: the one you outlined in (b), or the one you outlined in (c)? Why?
Either plan would create incentive compatibility, but the one described in part (c) would do so by raising prices, rather than lowering them. Raising prices would be the better option.
London’s Market Bar has a unique pricing system where a computer sets the price based on demand. When demand picks up, the computer begins to gradually reduce prices. This pricing strategy is puzzling to those who have studied supply and demand. Celene Berman, the assistant manager, says a group of “young city-
boy types” recently kept asking why prices “were going the wrong way around.” Explain, using your knowledge of block pricing, why the owner’s strategy of reducing prices as sales increase might actually lead to increased profit for the bar. Microsoft sells two types of office software, a word processor it calls Word, and a spreadsheet it calls Excel. Both can be produced at zero marginal cost. There are two types of consumers for these products, who exist in roughly equal proportions in the population: authors, who are willing to pay $120 for Word and $40 for Excel, and economists, who are willing to pay $50 for Word and $150 for Excel.
Ideally, Microsoft would like to charge authors more for Word and economists more for Excel. Why would it be difficult for Microsoft to do this?
It may be difficult for Microsoft to be able to observe a customer’s demand type before purchase.
Suppose that Microsoft execs decide to sell Word and Excel separately. What price should Microsoft set for Word? (Hint: Is it better to sell only to authors, or to try to sell to both authors and economists?) What price should Microsoft set for Excel? What will Microsoft’s profit be from a representative group of one author and one economist?
Word should cost $120, so that only authors buy it, and Excel should cost $150, so that only economists purchase it. The profit is $120 + $150 = $270, since ATC and MC are zero. To sell Word to both groups, the price must equal the maximum willingness to pay of the group which values Word less than Excel; that is, $50. Hence, Word would be sold to both groups and the profit would be $50 + $50 = $100; that is, $20 less than if the price were set at $120. Similarly for Excel, if the price were set at $40, so that both groups would be willing to buy it, the profit would be $80 instead of $150.
Suppose that Microsoft decides to bundle together Word and Excel in a package called Office, and not offer them individually. What price should Microsoft set for the package? Why? How much profit will Microsoft generate from a representative group of one author and one economist?
The price for Microsoft Office should be $160, so that both groups, authors and economists, would be willing to buy the product.
Does bundling allow Microsoft to generate higher profit than selling Word and Excel separately?
The profit from selling the bundled Office to a representative group of one author and one economist is $320. Compared to the $270 profit available from selling Word and Excel separately [see part (a)], bundling generates higher profit.
Three consumers, John, Kate, and Lester, are in the market for two goods, dates and eggs. Their willingness to pay for dates and eggs is given in the table below:
Dates (1 package) Eggs (1 dozen) John $0.60 $2.00 Kate $1.30 $1.30 Lester $2.00 $0.60 419
If you are a local farmer who can produce dates and eggs for free, what is the optimal price for dates and eggs if you price them individually? How much profit will you generate?
If you bundle dates and eggs together, what price should you set for a bundle containing one package of dates and a dozen eggs? How much profit will you generate?
Is there any advantage to mixed bundling in this case? Why or why not?
Suppose that the cost of producing dates and eggs rises to $1.00 per package and $1.00 per dozen, respectively. Now is there any advantage to mixed bundling? Why or why not? Explain your answer with a numerical illustration.
What accounts for the change in optimal strategy when costs change?
Elario makes delicious cupcakes that he mails to customers across the country. His cupcakes are so delicious that he has a great degree of pricing power. Elario’s customers have identical demands for cupcakes. A representative customer’s demand is shown in the diagram below. Elario can make a cupcake for a constant marginal and average total cost of $0.50.
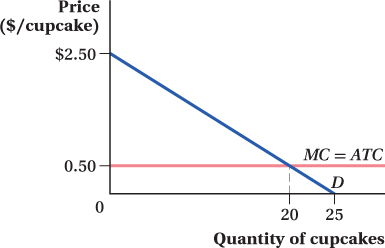
If Elario is an ordinary monopolist, what price should he charge for cupcakes? How many will each customer order? How much profit will Elario earn? How much consumer surplus will the buyer get?
The inverse demand function is P = 2.5 – 0.1Q.
Thus, the marginal revenue is
MR = 2.5 – 0.2Q
The profit-
maximizing quantity is MR = 2.5 – 0.2Q = 0.5 = MC
Q = 10
The profit-
maximizing price is 2.5 – (0.1 × 10) = $1.50
The profit from the representative customer is
TR – TC = (P – ATC) × Q = ($1.50 – $0.50)
× 10 = $10
The consumer surplus is area A.
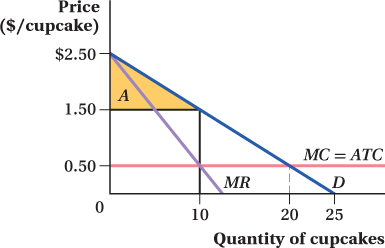
Thus, the consumer surplus is
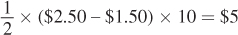
Suppose that Elario decides to offer a quantity discount according to the following terms: The first 10 cupcakes can be bought for $1.50 each; any cupcake over 10 will be offered at a discounted price. What discount price will maximize Elario’s profit from this pricing scheme? (Hint: Draw a new demand curve for Elario’s customers’ demand, but because his customers have already purchased 10, begin your demand curve at the 11th unit. Alternatively, shift the vertical axis to the right by 10 units.)
b. and c. The demand function does not change. Consider the “discounted” part of the demand function.
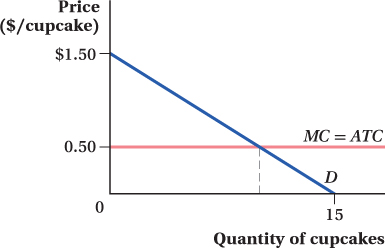
The new inverse demand function is P = 1.5 – 0.1Q.
Thus, the marginal revenue is
1.5 – 0.2Q
The profit-
maximizing quantity is MR = 1.5 – 0.2Q = 0.5 = MC
Q = 5
The profit-
maximizing price is 1.5 – (0.1 × 5) = $1
At full price, each consumer will order 10 cupcakes and at the discounted price 5 cupcakes.
How many cupcakes will customers order at full price? How many at the discounted price?
b. and c. The demand function does not change. Consider the “discounted” part of the demand function.

The new inverse demand function is P = 1.5 – 0.1Q.
Thus, the marginal revenue is
1.5 – 0.2Q
The profit-
maximizing quantity is MR = 1.5 – 0.2Q = 0.5 = MC
Q = 5
The profit-
maximizing price is 1.5 – (0.1 × 5) = $1
At full price, each consumer will order 10 cupcakes and at the discounted price 5 cupcakes.
What will Elario’s profit be? How does this scheme compare to the profit he earned as an ordinary monopolist?
b. and c. The demand function does not change. Consider the “discounted” part of the demand function.

The new inverse demand function is P = 1.5 – 0.1Q.
Thus, the marginal revenue is
1.5 – 0.2Q
The profit-
maximizing quantity is MR = 1.5 – 0.2Q = 0.5 = MC
Q = 5
The profit-
maximizing price is 1.5 – (0.1 × 5) = $1
At full price, each consumer will order 10 cupcakes and at the discounted price 5 cupcakes.
Suppose that Elario gets super greedy and decides to implement a three-
tiered pricing system. What three prices should he choose to maximize his profit? At what quantities will the price points change? What will his profit be? The profit from this two-
tiered pricing plan is $10 + ($1 – $0.50) × 5 = $12.50
Having introduced the discounted price for cupcakes, Elario has increased his profit by $2.50.
SB-
18 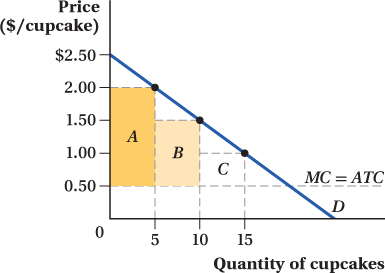
To implement a three-
tiered pricing system, simply split the demand curve above marginal cost into four equal parts, as shown in the graph above. Elario will set the price points as follows: $2 for the first 5 units, $1.50 for the next 5, and $1 for any quantity more than 10. Consumers will purchase 15 units in all. Elario will earn 5 × ($2 – $0.50) = $7.50 (shown as area A) on the first 5 units sold; he will earn 5 × ($1.50 – $0.50) = $5 (shown as area B) on units 6 through 10, and 5 × ($1 – $0.50) = $2.50 (shown as area C) on the remaining 5 units. Elario’s total profit will be $15. He earns more profit with a three- tiered pricing system than he did with a two- tiered system. Suppose Elario decides to charge $2.40 for the first cupcake, $2.30 for the second, and so on. How many cupcakes will he sell, and what will his profit be?
Elario is essentially adopting a 20-
tiered pricing system. He will sell one cupcake at $2.40, the next at $2.30, and so on, working his way down the customer’s demand curve one unit at a time. He will stop cutting the price when it dips below his cost of production: In total, he will sell 20 cupcakes and the price of the last cupcake will be $0.50. Accounting for his cost of production, he will earn a profit of $1.90 + $1.80 + . . . + $0.10 + $0. This all adds up to $19.00 profit.
What happens to consumer surplus as Elario adds more price points? Where does it go?
The consumer surplus decreases and is captured as profit by Elario. The pricing strategy should eliminate all deadweight loss as well, captured as profit by Elario.
-
Consider the demand for cupcakes in Problem 16. Suppose Elario decides to sell cupcakes only in packages of 20.
How much would customers be willing to pay to obtain a 20-
pack of Elario’s cupcakes? (Hint: Remember that the value of each cupcake is given by the corresponding point on the demand curve. Add up those values for cupcakes 1– 20.) How much profit will Elario earn from each customer?
How does the profit from this scheme compare to the profit Elario earned in part (f) of Problem 16?
Many gyms offer a mixed two-
part tariff pricing scheme. One can join the gym and then have daily access at a very low cost (often, free); alternatively, one can choose not to join and pay a higher daily fee (perhaps $10 or $15). Explain the rationale for this dual pricing scheme. What must be true of the gym’s customers’ demands? 420
Nathan sells gourmet hot dogs. His customers have identical inverse demands, given by P = 5 – 0.25Q. Nathan can produce hot dogs at a constant marginal and average cost of $1.
If Nathan operates as a single-
price monopolist, what price should he set? How many units will he sell? What will his profits be? Suppose Nathan decides to create a hot dog club where members pay an annual enrollment fee and are then entitled to buy as many hot dogs as they wish at a fixed price. If Nathan chooses a fixed price of $2.00 per hot dog, what is the maximum membership fee he will be able to charge his customers? How much profit will Nathan earn from each customer? (Hint: Add Nathan’s profits from selling hot dogs to the membership fee.) How do Nathan’s profits compare to what he earned in (a)?
If Nathan chooses a fixed price of $1.00, what membership fee will he be able to charge his customers? What will his overall profits be?
Can Nathan increase his profits by charging a super-
high admission fee and giving away hot dogs to members for free? Generalize a rule about the per-
unit price and membership fee that will maximize profits for a seller implementing a two- part tariff.
-
Identify the pricing strategy each seller uses in the following items:
A local bar hosts “Ladies’ Night” where women pay half-
price. A local tire store offers Firestone tires at $160 each, or $400 for a set of 4.
The Sands, a local country club, charges $4,000/year to join, plus a $30 greens fee each time you play a round of golf.
Charmin Ultra toilet paper is sold only in 12-
roll packages. At Denny’s, you can order a bacon and egg breakfast, but you can also order bacon and eggs individually.
Lie-
Nielsen Toolworks sells a handplane made of ordinary cast iron, but for a premium price you can buy the same plane in beautiful cast bronze.
For each situation below, identify an appropriate pricing strategy the firm could use to increase profits, if any:
All Krispy Kreme customers have identical demands.
Some movie buffs like action movies and love spy thrillers; others love action movies and like spy thrillers. Unfortunately, DVD movie seller Best Buy cannot tell who is who.
AMC Theatres knows that working professionals have a less elastic demand for movie tickets than students and senior citizens.
Some buyers of toner cartridges don’t print very often, only printing documents that are very important. Other buyers print often and purchase many toner cartridges; those buyers are quite price-
sensitive. McGraw-
Hill, publisher of college textbooks, knows there is a very active secondary market in used textbooks.
 Work this problem with calculus
Work this problem with calculus