In the previous section, we learned that the collusion/cartel model of oligopoly in which firms behave like a monopoly is unlikely to hold in reality. If firms don’t (or can’t) cooperate to act as a single monopolist would, we need a model in which they compete directly against one another. The first such model is as simple as it gets: Firms sell the same product, and consumers compare prices and buy the product with the lowest price. Economists call this structure Bertrand competition, after Joseph Bertrand, the nineteenth-century French mathematician and economist who first wrote about it. When firms are selling identical products, as we’re assuming here, Bertrand oligopoly has a particularly simple equilibrium: P = MC, just like perfect competition. In later sections of this chapter, we see how things change when firms sell products that are not identical.

To set up this model, let’s suppose there is a market with only two companies in it. They sell the same product and have the same marginal cost. For example, suppose there are only two stores in a city, a Walmart and a Target, and these stores are located next to each other. They both sell Sony PS4s. Each firm’s marginal cost is $150 per console. This includes the wholesale price the firm has to pay Sony as well as miscellaneous selling costs such as stocking the consoles on shelves, checking customers out, and so on.

433

We need one further assumption: Consumers don’t view either store differently in terms of service, atmosphere, and the like. If consumers did value these things separately from the video games, then in a way the products would no longer be identical and we would need to model the firms’ behavior using the model of differentiated products discussed later in the chapter.

With only two companies in a market, it might seem as if there would be a lot of market power and high markups over cost. But suppose the customers in this market have a simple demand rule: Buy the PS4 from the store that sells it at the lowest price. If both stores charge the same price, consumers flip a coin to determine where they buy. This rule means, in effect, that the store charging the lowest price will get all the demand for PS4s in the market. If both stores charge the same price, each store gets half of the demand.

Suppose the total demand in the market is for Q consoles. Let’s denote Walmart’s price as P_W and Target’s price as P_T. The two stores then face the following demand curves:

Demand for PS4s at Walmart:

Q, if P_W < P_T

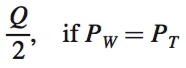
0, if P_W > P_T

Demand for PS4s at Target:

Q, if P_T < P_W

0, if P_T > P_W

Each store chooses its price to maximize its profit, realizing that it will sell the number of units according to the demand curves above. We’ve assumed the total number of consoles sold, Q, doesn’t depend on the price charged. The price only affects which store people buy from. (We could alternatively have allowed Q to depend on the lowest price charged; all of the key results discussed below would remain the same.)

Remember that in a Nash equilibrium, each firm is doing the best it can given whatever the other firm is doing. So to find the equilibrium of this Bertrand model, let’s first think about Target’s best response to Walmart’s actions. (We could do this in the other order if we wanted.) If Target believes Walmart will charge a price P_W for PS4s, Target will sell nothing if it sets its price above P_W, so we can probably rule that out as a profit-maximizing strategy. Target is left with two options: Match Walmart’s price and sell Q/2 units, or undercut Walmart and sell Q. Because all it has to do is undercut Walmart by any amount, dropping its price just below P_W will only reduce its per-unit margin by a tiny amount, but the store will double its sales because it will take the whole market instead of splitting it.

As an example, suppose Q = 1,000 and Target thinks Walmart will charge P_W = $175. If Target also charges P_T = $175, it will sell 500 PS4s at a profit of $25 each (the $175 price minus the $150 marginal cost). That’s a total profit of $12,500. But if Target charges $174.99, it will sell 1,000 PS4s at a profit of $24.99 each. This is a profit of $24,990—almost double what it was at $175. Target has a strong incentive to undercut Walmart’s expected price.

434

Of course, things are the same from Walmart’s perspective: It has the same incentive to undercut whatever price it thinks Target will choose. If it believes Target is going to charge P_T = $174.99 for a PS4, Walmart could price its consoles at $174.98 and gain back the entire market. But then Target would have the incentive to undercut this expected price, and so on.

This incentive for undercutting would only stop once the price each store expects the other to charge falls to the level of the stores’ marginal costs ($150). At that point, cutting prices further would let a store gain the entire market, but that store would be selling every PS4 at a loss (try to make that up on increased volume!).

The equilibrium of this Bertrand oligopoly occurs when each store charges a price equal to its marginal cost—$150 in this example. Each obtains half of the market share, and each store earns zero economic profit. The stores would like to charge more, but if either firm raises its price above marginal cost by even the smallest amount, the other firm has a strong incentive to undercut it. And dropping prices below marginal cost would only cause the stores to suffer losses. So the outcome isn’t the most preferable outcome for the firms, but neither firm can do better by unilaterally changing its price. This is the definition of a Nash equilibrium.

In the identical-good Bertrand oligopoly, one firm cannot increase its profit by raising its price if the other firm still charges a price equal to its marginal cost. If the firms could somehow figure out a way to coordinate changes in their actions so that they both raised prices together, they would raise their profits. However, the problem with this strategy, as we saw earlier, is that collusion is unstable. Once the firms are charging prices above marginal cost, a firm can raise its profits by unilaterally changing its action and lowering its price just slightly.

The Bertrand model of oligopoly shows you that even with a small number of firms, competition can still be extremely intense. In fact, the market outcome of Bertrand competition with identical goods is the same as that in a perfectly competitive market: Price equals marginal cost. This super-competitiveness occurs because either firm can steal the whole market away from the other by dropping price only slightly. The strong incentive to undercut the price leads both firms to drop their prices to marginal cost.

This example had only two firms, but the result would be the same if there were more. The intuition is the same: Every firm’s price-cutting motive is so strong that the only equilibrium is for them to all charge a price equal to marginal cost, leading them to split the market evenly.7 The strong assumptions of the Bertrand model with identical products are rare in the real world, but markets that approximate this condition are online shopping sites that allow buyers to directly compare identical products made by different firms. Because the lowest-priced seller would take the lion’s share of the market in such situations (due to the ease with which consumers can compare and substitute among the choices), these markets often end up with all firms charging the same price, as the model predicts.