Problems

504

(Solutions to problems marked * appear at the back of this book. Problems adapted to use calculus are available online at www.macmillanhighered.com/launchpad/gls2e)

  1. Consider the game below:

    Duvall
    Stop Drop Roll
    Earl Hammer 4 , 14 9 , 6 5 , 3
    Anvil 8 , 2 6 , 12 1 , 7
    Stirrup 11 , 5 16 , 3 9 , 8

    1. Who are the players in this game?

      The players are Duvall and Earl.

    2. What strategies are available to Duvall?

      Duvall’s strategies are Stop, Drop, and Roll.

    3. If Earl plays “Hammer” and Duvall plays “Roll,” then what is Earl’s payoff?

      If Earl plays Hammer and Duvall plays Roll, Earl’s payoff is 5.

    4. If Earl plays “Stirrup” and Duvall plays “Drop,” what is Duvall’s payoff?

      If Earl plays Stirrup and Duval plays Drop, Duvall’s payoff is 3.

  2. For each player in the following games, find the dominant strategy, if any.

    1. Coyote
      Anvil Dynamite
      Roadrunner Beep 6 , 2 4 , 5
      Run 7 , 3 6 , 8

    2. Bart
      Pout Whine
      Maggie Lay Finger on Butterfinger 6 , 8 11 , 3
      Ignore Butterfinger 2 , 6 9 , 5

    3. Martha
      Red White
      Julia Steak 5 , 2 8 , 4
      Chicken 6 , 1 7 , 3

  3. Consider the following game:

    Fireman Sam
    Stop Drop Roll
    Mr. Benn Try on Costume 12, 7 8, 6 5, 2
    Look for Adventure 11, 16 6, 1 21, 8
    Hesitate 1, 3 4, 2 9, 4
    Open the Door 2, 8 11, 5 8, 7

    1. Find each player’s dominant strategy, if any.

    2. Find any dominated strategies.

  4. For each of the following games, use dominance to find the Nash equilibrium. Each game contains only one Nash equilibrium.

    1. MacBeth
      Clean Spot Listen to Wife
      MacDuff Slay King 10 , 2 8 , 4
      Roll Head 6 , 4 4 , 5

      Both players have dominant strategies. MacDuff’s dominant strategy is Slay King. MacBeth’s dominant strategy is Listen to Wife. Therefore, by dominance, the Nash equilibrium of this game is (8, 4) or (Slay King, Listen to Wife).

    2. Ferris
      Twist Shout
      Elvis Bump 4 , 8 6 , 6
      Grind 2 , 4 4 , 3

      Both players have dominant strategies. The dominant strategy for Elvis is Bump. Ferris’s dominant strategy is Twist. Therefore, by dominance, the Nash equilibrium for this game is (4, 8) or (Bump, Twist).

    3. Eagle
      Take It Easy Take It to the Limit
      Matthew Get Under Table 5 , 3 3 , 2
      Stand Up 3 , 5 14 , 4

      Only Eagle has a dominant strategy in this game, namely Take It Easy. Given that Eagle will always play Take It Easy, the best choice for Matthew is Get Under Table. Therefore, by dominance, the Nash equilibrium in this game is (5, 3) or (Get Under Table, Take It Easy).

  5. Use the check method to find the Nash equilibrium or equilibria (if any) in each of the following games:

    1. Fred
      Opera Bowling
      Wilma Opera 5 , 2 0 , 0
      Bowling 0 , 0 2 , 5

      When Wilma chooses Opera, Fred’s best response is to also choose Opera. When Wilma chooses Bowling, Fred’s best response is to also choose Bowling. Similarly, when Fred chooses Opera, Wilma should also choose Opera, and when Fred chooses Bowling, so should Wilma. Therefore, there are two Nash equilibria, (Opera, Opera) and (Bowling, Bowling).

    2. Chuck
      Straight Swerve
      Ren Straight 0 , 0 3 , 1
      Swerve 1 , 3 2 , 2

      When Ren chooses Straight, Chuck’s best response is to choose Swerve. When Ren chooses Swerve, Chuck should choose Straight. If Chuck chooses Straight, Ren should play Swerve, and when Chuck chooses Swerve, Ren should play Straight. Therefore, there are two Nash equilibria, (Swerve, Straight) and (Straight, Swerve).

  6. Work this problem with calculus

    Consider the game below:

    Ethel
    Left Right
    Fred Up 100 , 50 130 , 8
    Down 150 , 6 –10,000 , 4

    1. What is the Nash equilibrium in this game?

    2. Explain why this game might reasonably end up at a non-equilibrium outcome. Whose play is likely to be responsible for that happening?

    505

  7. You and a classmate (let’s call him Dave) discover that your economics teacher has been secretly talking about notions such as “love,” “fairness,” and “decency.” Desperate to preserve his reputation in the community of economists, he tries to buy your silence in the following way. “You two sit silently at a table. I’ll put down a hundred-dollar bill. You can take the bill, or pass the decision to Dave. Before Dave decides, I’ll put another hundred-dollar bill on the table. If he passes, I’ll add yet another bill to the table and you can have another turn. The game will end when someone takes the money, or when the $500 in my wallet is gone, whichever comes first.” You both agree to keep quiet about your instructor’s transgressions for the chance to play the game, and as your teacher indicated, you get the first turn.

    1. Suppose that each of you has passed twice, and your instructor has just put the last $100 bill on the table. It is your turn: What should you do?

    2. Suppose that you have passed twice, and Dave has passed once. Your instructor has just put the fourth $100 bill on the table. What should Dave do: Take the money or pass? Why?

    3. Suppose that you and Dave have each passed once. Your instructor has just put the third $100 bill on the table. What should you do: Take the money or pass? Why?

    4. Suppose that you have passed once. Your instructor has just put the second $100 bill on the table. What should Dave do: Take the money or pass? Why?

    5. Your instructor has just laid the first $100 bill on the table. It is your turn. Should you take the money or pass? Why?

    6. What is the likely outcome of this game? Does your instructor pay the entire $500 for your silence?

  8. Consider the situation the economics professor faces in Problem 7, but now let’s suppose that Dave makes you the following offer: “Let’s really soak this guy. I’ll pass on turns 2 and 4 if you’ll go halves on the 500 bucks with me.” Should this offer fundamentally alter the outcome of the game? (Hint: Think about this problem using backward induction!)

  9. Trim the branches in the following game tree to solve the game depicted:

    image

  10. Each day, you and a friend play odds/evens to see who gets the last doughnut. On command, you each extend either one or two fingers. If the sum of the fingers is odd, you get the doughnut. If the sum of the fingers is even, your friend gets the doughnut.

    1. Let the payoffs from winning be 1, and from losing, 0. Fill in the payoff matrix below:

      You
      One Finger Two Fingers
      Friend One Finger
      Two Fingers

    2. Find the pure-strategy Nash equilibria in this game, if any.

    3. If you always play one finger, how will your friend respond? How much can you expect to win, on average?

    4. If you always play two fingers, how will your friend respond? How much can you expect to win, on average?

      506

    5. If you mix one finger and two fingers 50:50, and your friend does the same, what fraction of the time will you emerge victorious? How much can you expect to win, on average? Does mixing give you a higher average payout than playing a pure strategy?

    6. Suppose your day-by-day mixture is as follows: 1, 2, 1, 2, 1, 2, 1, 2. Will your 50:50 mixture give you a higher payout than playing a pure strategy? Why or why not?

    7. Economist Avinash Dixit claims that there is no better way to surprise your opponent than to surprise yourself. Suggest an easy way to randomize your play that gives you a 50:50 mix overall, but that does so in an unpredictable fashion.

  11. Your little twin sisters (whom you lovingly refer to as Thing 1 and Thing 2) are driving you crazy! You’ve baked them a lovely birthday cake, but they won’t stop fighting over who gets the biggest slice. To settle the dispute, you draw on a time-honored ritual: You ask Thing 1 to cut the cake, and Thing 2 to choose which piece she wants.

    1. Draw the extensive form of this game. Let Thing 1’s strategies be “Cut Evenly” or “Cut Unevenly”; depending on what’s on the platter, Thing 2’s strategies might include “Take Big Slice,” “Take Small Slice,” or “Take Equal Slice.” Assign payoffs to Thing 1 and Thing 2 that grow with the size of the slice they receive.

      image

    2. Use backward induction to find the equilibrium outcome for this game. Is the equilibrium consistent with your experience?

      The equilibrium outcome for this game is (2, 2) or (Cut Evenly, Equal Slice), so Thing 1 and Thing 2 take equal slices. The reason is that in the case of an uneven split, the second-mover will always choose the larger piece. Thus, the first-mover knows that she will end up with a smaller piece if she doesn’t cut evenly. Therefore, her best move is to cut the cake evenly. This is consistent with my experience.

    3. After the rules are announced, Thing 2 says, “It’s not fair! I want to be the one who gets to cut the cake, not the one that chooses the slice!” Is Thing 2’s complaint valid—in other words, is there a first-mover advantage in this game?

      Given the discussion in (b), the equilibrium outcome of this game will always be for the cutter to cut even slices, no matter who is the first-mover. Therefore, there is no first-mover advantage here.

  12. Crazy Eddie and Loopy Larry are two electronics merchants who sell plasma TVs at either a high price or a low price. If they both charge a high price, they will each earn high profits. If one charges a high price while the other charges a low price, the low-price seller will get all the business and earn a huge profit. If they both charge low prices, their customers get great deals and the merchants each earn a modest profit.

    1. Draw the extensive form of the game between Crazy Eddie and Loopy Larry. Assume that Crazy Eddie moves first and can choose a high price or a low price. Loopy Larry then follows with a high price or a low price.

    2. Find the equilibrium outcome in the battle between Crazy Eddie and Loopy Larry.

    3. In a series of wild TV commercials, Crazy Eddie announces, “Crazy Eddie will not be undersold! Find a better price, and I will match it!” Loopy Larry responds with the same offer. Redraw the game these two cutthroat competitors play, but give each player the chance to match his competitor’s price if he prices high and his competitor prices low.

    4. Find the equilibrium outcome in the battle between Crazy Eddie and Loopy Larry. Has the price-matching guarantee been good for consumers? Is price-matching indicative of intense competition?

  13. After years of training, Sara has landed a contract playing professional lacrosse. Eager to leverage her pro status by bringing in endorsements, she asks Jenny MacGuire to be her personal manager. Jenny has offered Sara a choice of two payment plans. Sara can engage Jenny’s services for a flat fee of $100,000. Alternatively, Sara can pay Jenny 15% of all endorsement revenue.

    Sara estimates that if Jenny expends modest effort ($20,000 worth) in her job, she will generate $600,000 in endorsement revenue for Sara. But if Jenny expends high effort ($50,000 worth), she’ll bring in $1 million in endorsements. On the day Sara and Jenny are to sign their agreement, Jenny tells Sara, “I am 100% dedicated to you, and will always work as hard as humanly possible on your behalf no matter what payment plan you choose.”

    1. Sara has a choice of payment plans; Jenny has a choice of effort levels. Determine the relevant payouts for all of the possible outcomes, and draw the extensive form of the game Sara and Jenny are playing.

    2. Find the equilibrium outcome to this game. Will Sara choose the flat fee or the 15% plan? Will Jenny expend modest effort or high effort?

    3. Is Jenny’s promise believable?

    4. Discuss the implications of the type of payment scheme on the incentives and payoffs each player faces. Then, extend your analysis by discussing paying workers an annual salary versus paying them a certain amount for each finished product they produce (called “piece-rate compensation”).

  14. Abel, Brenda, and Carlos are members of the Human Resources Management Club at their university. The club plans to bring a motivational speaker to campus with money earned selling doughnuts at the local farmers’ market. If the club sells doughnuts on three weekends, it will be able to afford a terrific speaker and Abel, Brenda, and Carlos will each get 100 units of happiness. If the club sells doughnuts on two weekends, it will be able to afford an above-average speaker that brings each member 70 units of happiness. If the club sells doughnuts on just one weekend, it will be able to bring in their college’s personnel director to speak and each member will receive 25 units of happiness. If the club doesn’t sell doughnuts at all, nobody will receive anything.

    507

    Abel is scheduled to sell doughnuts the first weekend, Brenda the second, and Carlos the third, after which the farmers’ market closes down for winter. Working at the farmers’ market costs the worker 40 units of happiness. On the scheduled day, each worker must choose between staffing the doughnut stand or sleeping in.

    1. Draw the extensive form of this game, with Abel moving first, Brenda second, and Carlos third.

    2. Solve for the equilibrium outcome of this game. What does each player do? What kind of speaker does the club bring in?

    3. Is there an advantage to being the first-mover in this game? Explain why or why not.

  15. Two graduate students are engaged to each other, and both are working on their master’s thesis—Kristen in political science and Michael in music education. Because both have incomes that are tied to their academic achievement, and because they plan to marry and share household income, each wants the other to complete their thesis. But Kristen is having a motivational crisis: She doesn’t want to complete her thesis.

    Kristen
    Complete Thesis Don’t Complete
    Michael Complete Thesis 11 , 6 8 , 8
    Don’t Complete 7 , 2 4 , 4

    1. How do the payoffs in the table reflect Kristen’s motivational crisis? Explain.

    2. What is the Nash equilibrium in this game?

    3. Michael would like Kristen to complete her thesis. He tells Kristen, “If you don’t complete your thesis, then I’m not going to complete mine.” Explain, using the numbers from the payoff matrix, why this threat is not immediately credible.

    4. Suppose that Kristen believes Michael’s threat. Explain, referring to the payoffs in the table above, why this threat should be sufficient to motivate Kristen to complete her thesis.

  16. Consider the game played by Michael and Kristen in Problem 15 above. Suppose that Michael decides not to threaten Kristen, but instead decides to promise her a monetary reward if she completes her thesis.

    1. How many points’ worth of money must Michael pay Kristen to convince her to complete her thesis?

    2. How many points’ worth of money is Michael willing to spend in order to convince Kristen to complete her thesis?

    3. Based on your answers to (a) and (b), can Michael and Kristen work out a mutually beneficial trade in which Michael gives Kristen money and she completes her thesis?

  17. Assume that two clothing manufacturers, Lands’ End and L.L. Bean, market their goods strictly by mail order. Each produces an essentially identical field coat. The cost of producing such a coat is exactly $100. Because the field coats are perfect substitutes, customers will flock to the seller that offers the lowest price. If both firms offer identical prices, each receives half the customers.

    For simplicity, assume that the two firms have the choice of pricing at whole-dollar prices of $103, $102, or $101. Market demand at $103 is 100 coats; at $102, 110 coats; and at $101, 120 coats. The profit each firm would earn at various prices is shown in the payoff matrix below:

    L.L. Bean
    $103 $102 $101
    $103 $150 , $150 $0 , $220 $0 , $120
    Lands’ End $102 $220 , $0 $110 , $110 $0 , $120
    $101 $120 , $0 $120 , $0 $60 , $60

    1. What is the equilibrium outcome of the game Lands’ End and L.L. Bean are playing?

    2. Is collusion between Lands’ End and L.L. Bean likely to last?

      508

    3. If Lands’ End and L.L. Bean were allowed to quote prices in cents rather than whole dollars, what would the likely outcome of this game be?

    4. Suppose that in hopes of raising prices above equilibrium, L.L. Bean decides to announce the price for its field coat early in the summer. Will that strategic move be successful for L.L. Bean? Why or why not?

  18. There are two ice cream vendors, Ben and Jerry, on a crowded strip of beach. There are five permissible locations for ice cream vendors to locate, cleverly named positions 1, 2, 3, 4, and 5. Position 1 is at the far north end of the beach, Position 5 at the far south end, and Position 3 in the middle, while Positions 2 and 4 are midway between their respective neighbors. Each location may accommodate more than one vendor. There are 1,000 beachgoers scattered uniformly across the beach (200 at each position) who will buy from the closest vendor.

    1. Fill in the payoff matrix below with payouts reflecting the number of customers each vendor receives. (Example: If Ben is at Position 1 and Jerry is at Position 4, Ben will get 400 beachgoers at locations 1 and 2, and Jerry will get 600 of the beachgoers at Positions 3, 4, and 5.)

      Jerry
      Position 1 Position 2 Position 3 Position 4 Position 5
      Ben Position 1
      Position 2
      Position 3
      Position 4
      Position 5

    2. Find the Nash equilibrium or equilibria in this game. Where are Ben and Jerry likely to end up locating?

  19. You are one of two member nations of OOEC: the Organization of Otter Exporting Countries, a cartel designed to artificially restrict otter output in an attempt to generate monopoly profits. Demand conditions are such that various combinations of output yield the profits in the payoff matrix below:

    Other Country
    Produce 1,000 Otters Produce 2,000 Otters
    Your Country Produce 1,000 Otters $500 , $500 $250 , $700
    Produce 2,000 Otters $700 , $250 $400 , $400

    1. If your country is able to successfully collude with the other country, how many otters will each country produce, and how much profit will each earn?

    2. What is the equilibrium outcome in this game if it is only played once? Is the equilibrium outcome a good one for your country?

  20. Refer to Problem 19. It seems realistic to assume that the game could continue indefinitely—after all, the world will need otters 50 years from now just as badly as it does today. But time is money, so a dollar of profit a year from now is only valued as much as $d received today, where d (the discount rate) is some amount less than $1.

    Assume that you adopt a grim trigger strategy whereby your country pledges to produce 1,000 otters as long as the other country produces 1,000 otters. But should the other country ever produce 2,000 otters, you will respond by producing 2,000 otters, forever and ever. After you announce your strategy, the other country pledges to abide by the grim trigger strategy.

    509

    1. What stream of profits will you generate if both countries adopt such a grim strategy? (Don’t forget to discount each year’s future profits by the appropriate multiple of d.) Express your answer as a sum.

      The sum should equal

      500 + d × 500 + d2 × 500 + . . .

    2. Suppose your country decides to take advantage of the other country’s pledge to reduce output by expanding your own output in the first year. What stream of profits can you expect to generate? Again, be sure to discount appropriately, and express your answer as a sum.

      The sum should equal

      700 + d × 400 + d2 × 400 + . . .

    3. Suppose d = 0.5. Are you better off cheating on your agreement, or abiding by it? How does your answer change if d = 0.99? What about d = 0.01?

      If d = 0.5, the sum from part (a) is equal to

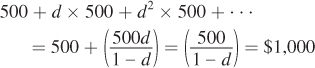
      image

      If you decided to cheat, you would get

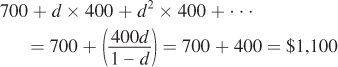
      image

      Thus, when d = 0.5, you should cheat. If d = 0.99, plugging 0.99 into the calculations above, we see that abiding gives us a payout of $50,000; cheating yields a payout of $40,300. Therefore, you should abide. If d = 0.01, abiding gives a payout of $505.05; cheating yields a payout of $704.04. You should cheat.

    4. At what level of d are you indifferent between cheating on or abiding by the agreement?

      Setting both sums from parts (a) and (b) equal to each other, we get

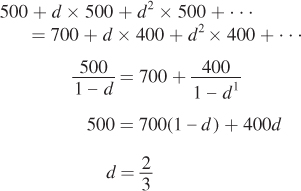
      image

      At 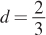image , you are indifferent between cheating or abiding by the agreement.

  21. In the 1960s, tobacco producers engaged in fierce battles for market share. The major weapon in that war was advertising—advertising that was designed not to attract new smokers, but to lure smokers away from competing brands. Consider the following scenario: There are two tobacco sellers, Phillip and R. J., each of whom can choose to advertise on TV (at a cost of $20 million) or not. There are $100 million of pre-advertising profits available to the two firms. If they both adopt the same budget, they will split the market evenly. If one chooses a high budget while the other chooses low, the high-budget firm will steal half the other’s customers and capture $75 million of pre-advertising profit; the other will earn $25 million. The firms’ net profits (after advertising expenses are considered) are illustrated in the payoff matrix below:

    R. J.
    Advertise Don’t Advertise
    Phillip Advertise $30 , $30 $55 , $25
    Don’t Advertise $25 , $55 $50 , $50

    1. Verify that the payoffs in the table reflect the story told above.

    2. What is the Nash equilibrium in this game? Is the equilibrium outcome a good one for anybody?

    3. Suppose that Phillip and R. J. promise each other that they will not advertise. Is such a promise credible? Explain.

    4. In 1971 the federal government banned cigarette advertising on TV. Initially, tobacco companies protested vehemently. Referring to the game table above, discuss whether Big Tobacco’s protests were genuine.