Problems
(Solutions to problems marked * appear at the back of this book. Problems adapted to use calculus are available online at www.macmillanhighered.com/
You are a bunny rancher.
Suppose that you have 100 bunnies, and that because of your successful animal husbandry, your stock of bunnies grows by 20% each year. How many bunnies will you have at the end of this year?
1. At the end of this year, you would have
100 + (100 × 0.2) = 100 × (1 + 0.2)
= 100 × 1.2 = 120 bunnies
Suppose that you have 120 bunnies, and that because of your successful animal husbandry, your stock of bunnies grows by 20% each year. How many bunnies will you have at the end of this year?
At the end of this year, you would have 120 + (120 × 0.2) = 120 × (1 + 0.2) = 120 × 1.2 = 144 bunnies.
Suppose that you have 100 bunnies, and that because of your successful animal husbandry, your stock of bunnies grows by 20% over the course of each year. How many bunnies will you have at the end of two years?
At the end of two years, you would have 144 bunnies, that is, 120 bunnies at the end of the first year and 144 at the end of the second year.
Suppose that you have 100 bunnies, and that your bunny stock grows by 20% per year. How many bunnies will you have at the end of 10 years?
At the end of 10 years, you would have
100 × (1 + 0.2)10 ≈ 619 bunnies
Imagine that you have $100 of ill-
gotten gains stashed in an offshore bank account. Lest the IRS get too nosey, you plan to leave that account idle until your retirement in 45 years. If your bank pays you 3% annual interest, what will your account balance be upon retirement?
If your bank pays you 6% interest, what will your account balance be upon retirement?
Does doubling the interest rate double your accumulated balance at retirement? More than double it? Less? Explain your answer.
Suppose that when you were one year old, your grandmother gave you a shiny silver dollar. Your parents put that silver dollar in a savings account with a guaranteed 9% interest rate, and then promptly forgot about it.
Use the Rule of 72 to estimate how much that account will grow to by the time you are 65.
Calculate exactly how much you will have in that account using the formula for compound interest.
How close are your answers to (a) and (b)?
You are writing the great American novel and have signed a contract with the world’s most prestigious publisher. To keep you on schedule, the publisher promises you a $100,000 bonus when the first draft is complete, and another $100,000 following revisions. You believe that you can write the first draft in a year and have the revisions done at the end of a second year.
If interest rates are 5%, what is the value today of the publisher’s future payments?
The value of the publisher’s future payments is
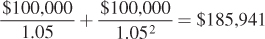
Suppose the publisher offers you $80,000 after the first draft and $125,000 following revisions. Is this a better deal than the original offer?
Considering the second offer, the value becomes
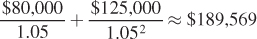
Hence, this is a better deal than the original one as $189,569 > $185,941. The net present value of the loss in payments of the first year (20,000/1.05) is more than compensated for by the net present value increase in payments offered in the second year (25,000/1.052).
A state lottery makes the following announcement: “Frederick Carbuncle has just won $100 million! We’ll pay Frederick $10 million each year for the next 10 years!”
Has Frederick really won $100 million? Explain.
Many state lotteries allow winners to choose a single payment instead of a series of annual payments. “We’ll offer you the present value of your annual payments, Frederick,” the lottery commissioner says. “And because we’re feeling generous, we’ll use a really high interest rate when we calculate how much that prize will be. Congratulations, Fred!” Comment on the generosity of the lottery commissioner.
You have just purchased a Kia with a $20,000 price tag. The dealer offers to let you pay for your car in five equal annual installments, with the first payment due in a year.
If the dealer finances your purchase at an interest rate of 10%, how much will your annual payment be?
How much would your payment be if you had purchased a $40,000 Camry instead of a $20,000 Kia?
How much would your payment be if you arranged to pay in 10 annual installments instead of 5? Is your payment cut in half? Why or why not?
How much would your payment fall if you paid $10,000 down at the time of purchase?
569
Many college graduates feel as if their student loan payments drag on forever. Suppose that the government offers the following arrangement: It will pay for your college in its entirety, and in return you will make annual payments until the end of time.
Suppose the government asks for $6,000 each year for all of eternity. If interest rates currently sit at 4%, what is the present value of the payments you will make?
Your college charges $140,000 for four years of quality education. Should you take the government up on its offer to pay for your college? What if your college charged $160,000?
As a New Year’s gift to yourself, you buy your roommate’s 1976 Ford Pinto. She has given you the option of two payment plans. Under Plan A, you pay $500 now, plus $500 at the beginning of each of the next two years. Under Plan B, you would pay nothing down, but $800 at the beginning of each of the next two years.
Calculate the present value of each plan’s payments if interest rates are 10%. Should you choose Plan A or Plan B?
Recalculate the present value of each plan’s payments using a 20% interest rate. Should you choose Plan A or Plan B?
Explain why your answers to (a) and (b) differ.
Ricardo is considering purchasing an ostrich, which he can graze for free in his backyard. Once the ostrich reaches maturity (in exactly three years), Ricardo will be able to sell it for $2,000. The ostrich costs $1,500.
Suppose that interest rates are 8%. Calculate the net present value of the ostrich investment. Does the NPV indicate that Ricardo should buy the ostrich?
Suppose that Ricardo passes on the ostrich deal and invests $1,500 in his next-
est opportunity: a safe government bond yielding 8%. How much money will he have at the end of three years? Is this outcome better or worse than buying the ostrich? Calculate the net present value of the ostrich if interest rates are 11%. Does the NPV method indicate that Ricardo should buy the ostrich?
If Ricardo passes on the ostrich deal and invests in a government bond yielding 11%, how much money will he have at the end of three years? Is this outcome better or worse than buying the ostrich?
Based on your answers to (b) and (d), how well does the NPV method capture the concept of opportunity cost?
Marian currently makes $40,000 a year as a tow truck driver. She is considering a career change: For a current expenditure of $30,000, she can obtain her florist’s license and become a flower arranger. If she makes that career change, her earnings will rise to $48,000 per year. Marian has five years left to work before retirement (you may safely assume that she gets paid once at the end of each year).
Calculate the net present value of Marian’s investment in floriculture if interest rates are 10%.
The net present value of Marian’s investment is
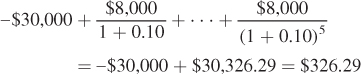
Assume that in terms of job satisfaction, floriculture and tow truck driving are identical. Should Marian change careers?
The net present value of Marian’s investment is $326.29. Therefore, Marian should change careers.
Compare the present value of Marian’s earnings as a tow truck driver to the present value of Marian’s earnings as a florist. Is the difference large enough to justify spending $30,000?
The present value of Marian’s earnings as a tow truck driver is
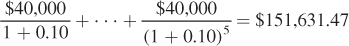
The present value of Marian’s earnings as a florist is
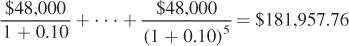
The difference of $181,957.76 – $151,631.47 = $30,326.29 is large enough to justify spending the $30,000.
Does the method you used in part (a) give an identical answer to the method you used in part (c)? Explain.
The methods used in parts (a) and (c) give precisely the same answer, $326.29:
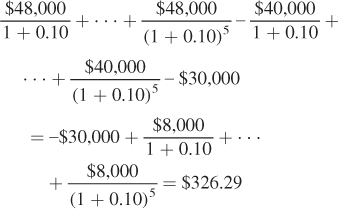
You are currently driving a gas-
guzzling Oldsmobuick that you expect to be able to drive for the next five years. A recent spike in gas prices to $5 per gallon has you considering a trade to a fuel- efficient hybrid Prius. Your Oldsmobuick has no resale value and gets 15 miles per gallon. A new Prius costs $25,000 and gets 45 miles per gallon. You drive 10,000 miles each year. Calculate your annual fuel expenditures for the Prius and the Oldsmobuick.
Assume that the interest rate is 7%. Calculate the present value of your costs if you continue to drive the Oldsmobuick for another five years. Assume that you purchase a new Prius at the end of the fifth year, and that a Prius still costs $25,000. Also assume that fuel is paid for at the end of each year. (Carry out your cost calculations for only five years.)
Calculate the present value of your costs if you purchase a new Prius today. Again, carry out your cost calculations for only five years.
Based on your answers to (b) and (c), should you buy a Prius now, or should you wait for five years?
Would your answer change if your Oldsmobuick got 30 miles per gallon instead of 15?
570
You have $832.66 in a savings account that offers a 5.25% interest rate.
If you leave your money in that account for 20 years, how much will you have in the account?
Suppose that inflation is expected to run at 3.25% for the next 20 years. Use the real interest rate to calculate the inflation-
adjusted amount your account will contain at the end of the 20- year period. The amount you calculated in (b) is smaller than the amount you calculated in (a). Explain exactly what the amount you calculated in (b) tells you, and why the difference arises.
Mel is a risk-
neutral investor concerned about the future availability of gas. He is considering purchasing a gallon of gas today and placing it in storage for 10 years as a hedge against future gas price increases. If today’s price of gas is $4.00 per gallon, and the future price of gas is $6.00 per gallon, is placing a gallon of gas in storage a good idea? Assume that the market interest rate is 4%.
Suppose that Mel is uncertain of the future price of gas. He estimates that there is a 0.1 probability that gas will continue to sell for $4.00 per gallon, a 0.4 probability that gas will sell for $5 per gallon, and a 0.5 probability that gas will sell for $6.80 per gallon. Should Mel place a gallon of gas in storage today? Will your answer be the same if Mel is risk-
averse?
You are romantically interested in Chris, but have always wanted to date the president of the Economics Club. As it turns out, Chris is battling Pat for control of the Econ Club. That battle should be decided in a year, and you estimate the odds of Chris winning at 60%. Attracting Chris and kindling a relationship will involve $1,000 of effort on your part; if Chris wins the presidency, you will receive benefits worth $2,200 (assume you receive these benefits one year after beginning the relationship). If Chris loses the election, you receive nothing.
Assume an interest rate of 10%. Calculate the net present value of building a relationship with Chris today. Notice that the costs of kindling a relationship today are certain, but the benefits are uncertain.
Considering only your answer to (a), should you initiate a relationship with Chris at this time? Assume you are risk-
neutral in formulating your answer. Calculate the net present value of waiting until the presidency is decided to build a relationship with Chris. Note that both the costs and benefits of kindling a relationship are uncertain at this point, but that the two will be certain in one year.
Based on your answers to both (a) and (c), should you initiate a relationship with Chris today, or should you wait to initiate the relationship until the presidency is determined?
You are considering the purchase of an old fire station, which you plan to convert to an indoor playground. The fire station can be purchased for $200,000, and the playground will generate lifetime profits (excluding the cost of the building) of $700,000. (Assume that those profits are all realized one year after opening.) However, there is a 20% chance that the city council will re-
zone the district to exclude establishments such as yours; a hearing is scheduled for the coming year, and if your building is re- zoned, your profit will be zero. Assume that there is no other building currently under consideration. Assume an interest rate of 10%. Calculate the net present value of opening the playground today. Note that the cost of purchasing the building today is certain, but the benefits are uncertain.
The NPV is
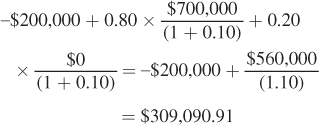
Calculate the net present value today of opening the playground in one year, after the zoning issues have been decided. Note that the benefits of opening the playground are uncertain today, but will be certain in one year.
The net present value today of opening the playground in one year is
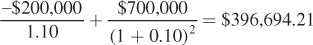
Based on your answers to (a) and (b), should you open the playground today, or should you wait until the zoning commission reaches its decision?
The NPV in part (b) is greater than the NPV in (a). Therefore, you should wait until the zoning commission reaches its decision.
Speedy Steve is a traveling salesman. His utility function is given by U = I0.5, where U is his utility and I is his income. Steve’s income is $900 each week, but if Steve is caught speeding while making his rounds, he will receive a hefty fine. There is a 50% chance he will be caught speeding in any given week and pay a fine of $500.
Calculate Steve’s expected income and expected utility.
Steve’s expected income is
$900 – 0.50 × $500 = $650
His expected utility can be found as follows. Half the time, he will receive 9000.5 or 30. The other half of the time, he will receive 4000.5 or 20:
U = 0.5 × 30 + 0.5 × 20 = 25
Suppose that Steve’s boss offers him a position in online sales that eliminates the risk of being caught speeding. What salary would provide Steve with the same utility he expected to receive as a traveling salesman?
A salary of $625 would provide Steve with the same utility he expected to receive as a traveling salesman because $6250.5 = 25.
Suppose instead that Steve was given the opportunity to purchase speeding ticket insurance that would pay all of his fines. What is the most Steve would be willing to pay to obtain this insurance? Explain how you arrived at this number.
Steve gets exactly the same utility from a risk-
free $625 a week as he does from a risky job where his earnings average $650. Given that he is expected to pay, on average, $250 to the traffic court each week anyway, he would be willing to pay an extra $25 in weekly earnings to avoid the uncertainty (since $900 – $250 = $650). Therefore, he should be willing to pay up to $275 for speeding ticket insurance. If the company issuing the insurance referred to in (c) convinces Steve to pay the amount you indicated, will the insurer earn a profit? If so, how much profit will it earn?
The insurance company would break even if the insurer charges Steve $250 each week. If the insurer can charge him the $275 he is willing to pay, it will earn a $25 profit.
571
Danielle is a farmer with a utility function of U = I0.5, where U is Danielle’s utility and I is her income. If the weather is good, she will earn $100,000. If there is a hailstorm, she will earn only $50,000. The probability of a hailstorm in any given year is 30%.
What is Danielle’s expected income if she is uninsured? Her expected utility?
Suppose a crop insurer makes the following offer to Danielle: In years when there is no hailstorm, Danielle pays the insurer $16,000. In years when there is a hailstorm, the insurer pays Danielle $34,000. What is Danielle’s expected income? Her expected utility?
Comment on the following statement referring to your answers to parts (a) and (b): “The insurance agreement in (b) reduces Danielle’s expected income. Therefore, it must make her worse off.”
Suppose instead the insurer offers Danielle the following: In years when there is no hailstorm, Danielle pays the insurer $10,000; in years when there is a hailstorm, the insurer pays Danielle $20,000. How does Danielle’s expected income and expected utility compare to the uninsured outcome in (a) and the insured outcome in (b)?