Principal–agent relationships are a common set of economic transactions involving asymmetric information. They exist whenever one party (the principal) hires another (the agent) to perform some task, and the principal has an asymmetric information problem because he cannot fully observe the agent’s actions (or, sometimes, the information the agent possesses). When this information asymmetry is combined with the fact that the principal’s and agent’s individual self-interests are usually not perfectly aligned, things become interesting.

634

There are many, many examples of principal–agent relationships. One of the most common, and the one on which we focus in this section, is between an employer and employee. An employer would like the employee to perform certain tasks. The employee likes to be paid for working, but might not prefer to work as hard or work at the same tasks as the employer would like him to.

The divergence in an employer’s preferences (let’s call our employer Yvonne) and those of her employee (let’s call her Jean) is not in and of itself a problem. The two could write an employment contract with Jean’s pay contingent on her completing a set of tasks or conveying certain information specified by Yvonne. Jean would then have strong incentives to do as Yvonne wished, and Yvonne would have to compensate Jean enough for her to be willing to complete the requested actions. The problem lies in the fact that, because of the information asymmetry, the principal (Yvonne) can’t ever know for sure if the agent (Jean) has done what she requested. Yvonne must instead infer the adequacy of Jean’s responses as best as she can, using only imperfect information about Jean’s job performance. For example, Yvonne can’t just observe sales and know exactly how hard Jean worked. Maybe Jean didn’t work hard, but other things caused sales to be high. Or, maybe Jean did work hard but other factors caused sales to be low. Yvonne can’t know for sure. While sales are likely to be correlated with Jean’s effort, they are also influenced by unrelated factors. This makes sales an imperfect measure for Yvonne to gauge Jean’s actual level of effort.

This logic carries over to other types of principal–agent relationships. A company’s shareholders—the principals in this case—want the CEO and management team (the agents) to take actions that maximize the market value of the company. But, management might want instead to use company resources to pay for personal perks, like fancy corporate dining rooms, unneeded corporate jets, and extravagant personal travel. If it’s not clear whether such expenses are justified—fancy dining rooms might help close big deals and corporate jets do save time, for example—shareholders can’t be certain that management is or isn’t acting fully in the shareholders’ interests.

The moral hazard problems facing insurers and their policyholders can also be cast as principal–agent relationships. Insurance companies (the principals) want policyholders (agents) to take actions to reduce risks. Because insurance companies typically can’t observe all these actions, a principal–agent problem exists.

What can the principals do in these situations? The principals know how they would like their agents to act. The problem is that the principals cannot fully observe what the agents do. Otherwise, the principals could simply make the agents’ payoffs conditional on taking the desired actions. Instead, the principals must somehow set up incentives to make it in the agents’ own best interests to take the actions that the principals desire.

Let’s consider a simple example. Suppose that the daily profit of a small mobile phone kiosk in the local mall is higher when the kiosk’s employee, Joe, works harder. (We’ll assume for simplicity that Joe is the only employee.) Joe can work hard, in which case the kiosk’s daily profit is $1,000 with 80% probability and $500 with 20% probability. (The latter might happen if it rains so traffic at the mall falls.) Alternatively, Joe could laze about by staring blankly at passersby and texting his friends. If Joe does so, the probability of the kiosk’s profit will be reversed: There will be 20% probability of a profit of $1,000 and 80% probability of $500. Joe doesn’t like to work hard; he has to be paid at least $150 before he’s willing to do so. Otherwise, he’s going to text his friends all day.

How should the kiosk’s owner (Selena, the principal) structure Joe’s (the agent’s) compensation? Remember, the root of the principal–agent problem is that the owner can’t perfectly observe the employee’s effort. Perhaps it’s too costly for Selena to monitor the kiosk all day long, or maybe Joe’s effort involves some dimension that is not readily apparent to Selena. Otherwise, Selena could simply require Joe to work hard, and pay him $150 if he does. Joe will be willing to accept this deal because he is being paid enough to compensate him for his cost of effort. Selena also likes this deal because inducing Joe to work hard raises her expected profit from $600 (0.2 × $1,000 + 0.8 × $500) to $900 (0.8 × $1,000 + 0.2 × $500), a $300 increase, but it only costs Selena at most $150 in wages.

635

When Joe’s effort is unobservable, however, his pay cannot be based on how hard he works. And, simply offering Joe a flat wage of $150 isn’t a solution either. Because he faces a cost of working hard but would take home the same pay regardless of whether he exerts any effort, he would choose to be lazy. This is clearly undesirable to Selena, who would pay $150 in wages but only earn the low expected profit of $600 rather than $900. When effort is unobservable, therefore, simply offering enough pay to compensate Joe for his effort does not actually lead to him working hard.

What Selena can do, however, is tie Joe’s pay to something she knows is related to Joe’s effort: namely, the kiosk’s profit. Because Joe can affect the likelihood that profits (and therefore his wages) are high by working hard, this offers him an incentive to exert effort. Of course, the extra wages he expects to earn working hard have to be high enough to compensate him for that extra effort.

Suppose Selena offers the following deal: Joe is paid $255 if the kiosk’s profits are high (i.e., $1,000) and $0 if profits are low ($500). What sort of behavior would this lead to? Think about Joe’s tradeoffs. If he works hard, he has an 80% chance of earning $255 and a 20% chance of earning nothing. His expected earnings are $204 (0.8 × 255 + 0.2 × 0). However, he also suffers an effort cost of $150, so his net gain from working hard is $54. If Joe chooses to be lazy, he will have an 80% chance of earning nothing and a 20% chance of earning $255, yielding expected earnings of $51. By being lazy, Joe pays no effort cost, so his net gain from being lazy is $51. Under this compensation plan, Joe prefers working hard to being lazy.

Does Selena also prefer this new plan? We already know that if Joe works hard, the kiosk’s expected profit will be $300 higher. Selena expects to pay Joe $204 (0.8 × 255 + 0.2 × 0) if he works hard. Thus, the new compensation scheme is worthwhile from Selena’s perspective, because by giving Joe the incentive to work hard, it raises her expected profit net of wages by $96.

Selena (the principal) can, in fact, give Joe (the agent) incentives to work hard. The key is to pay him much more when observable events occur that are correlated with his unobservable effort (i.e., when profit is high because Joe works hard). By tying the agent’s compensation to outcomes that the principal likes, the principal aligns the agent’s incentives on the margin with her own.

This example, as with more general principal–agent problems, can also be thought of as a sequential game (see Chapter 12). The first mover in a principal–agent game is the principal, and the strategy he chooses is the agent’s compensation structure. Given the principal’s chosen compensation structure, the agent then chooses his strategy, which we can think of as effort or, more generally, any action that improves the principal’s payoff. Taking this action may be costly for the agent, however, and the principal does not directly observe it. Payoffs are realized for both players based on the action chosen by the agent.

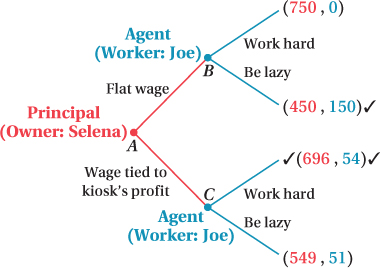
Figure 16.2 shows the game tree for the interaction between the mobile phone kiosk owner, Selena, and her employee, Joe. Selena moves first; she has the choice of paying Joe a flat wage of $150 that doesn’t depend on the kiosk’s profit or a wage that is tied to the kiosk’s profit: $255 if profit is high and $0 if it is low. Once the compensation structure is chosen, Joe then chooses his effort level: high or low. Given this choice, Selena and Joe earn their expected payoffs.

636

As with any sequential game, we can find the equilibrium using backward induction. Suppose Selena chooses the flat $150 pay structure. If Joe works hard, Selena’s expected payoff is $750 (the $900 profit from the kiosk minus the $150 wage she pays Joe), and Joe’s payoff is $0 (his $150 wage minus his $150 effort cost of working hard). If Joe chooses to be lazy, Selena’s expected payoff is $450 ($600 kiosk profit minus wages of $150), while Joe’s payoff is $150 (his wage alone, because he has no cost of effort). Selena prefers Joe to work hard, but Joe’s payoff is greater from being lazy. As a result, Joe chooses to be lazy under this compensation plan.

Now suppose Selena chooses to link Joe’s pay to the kiosk’s profit: Joe receives $255 for high profit and $0 for low profit. Joe works hard in this case, Selena’s expected payoff is $696 ($900 in expected kiosk profit minus the expected $204 in pay to Joe), and Joe’s expected payoff is $54 (his $204 expected wage minus his $150 effort cost of working hard). If Joe chooses to be lazy, Selena’s expected payoff is $549 ($600 kiosk profit minus wages of $51), while Joe’s expected payoff is $51. Joe’s expected payoff from working hard is higher in this scenario, so he makes the extra effort and raises the kiosk’s expected profit.

Now that we’ve solved for the last stage of the game, we can figure out Selena’s equilibrium action in the first stage. If she chooses the flat $150 pay structure, Joe doesn’t work hard and her expected payoff is $450. If Selena chooses to link pay to the kiosk’s performance ($255 for high profit and $0 for low profit), then Joe works hard and her expected payoff is $696. Therefore, Selena’s optimal action in the first stage is to choose the performance-linked pay structure.

That’s the equilibrium of this principal–agent game: Selena chooses a pay structure that links Joe’s compensation to an observable outcome, the kiosk’s profits, that is correlated with Joe’s unobservable effort. In response to this choice, Joe exerts the amount of effort the owner desires.

Again, what Selena would really prefer is to monitor Joe’s effort directly, specify that he works hard as a condition of employment, and pay a flat wage of $150 to compensate Joe for working hard. In this case, Selena’s expected payoff would be $750, higher than in the equilibrium above. Selena can’t do this, however, because she is unable to continuously monitor Joe’s effort. As a result of the principal–agent problem, Selena is left with the second-best outcome, a $696 expected payoff.

637

The Selena–Joe example is simple: It has only two outcomes (high or low profits) and two choices for the agent (high or low effort). However, its insights hold in more general settings with multiple possible outcomes and a range of agent choices. The optimal compensation structure fully aligns the marginal incentives of the agent with those of the principal. In other words, principals want to design compensation structures that make agents face the same incentives the principals would face if they were making the agents’ choices for them. When this is not the case, the principals’ and agents’ incentives are misaligned and can lead to inefficient outcomes.

You might wonder, if principal–agent situations are so common, especially in employment relationships, why pay-for-performance (or maybe pay-for-outcome is more accurate) isn’t the norm. Certainly, many people in sales professions have their pay tied directly to outcomes related to their performance through commissions. Some workers also get paid piece rates, where they are paid a set amount per unit of work they complete (e.g., per dress sewn). But, many people are paid a fixed hourly wage or even an annual salary. Does this mean that there is no principal–agent dynamic involved in those jobs? Well, there might be less of an issue, but other “levers” are available to tie job outcomes to compensation. Annual bonuses, promotions, stock options, deferred compensation, and threats of being fired all serve as ways that employers can give workers the incentives to perform as the employer wishes. So when you are looking for evidence of principal–agent relationships, be sure to consider the full range of tools the principal has available to induce the agent to behave in a way (unobservable by the principal) that results in the best outcome for the principal.

638

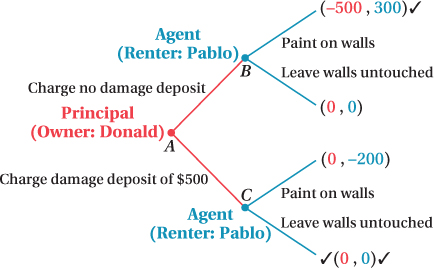
639