Problems
(Solutions to problems marked * appear at the back of this book. Problems adapted to use calculus are available online at www.macmillanhighered.com/
Kansas City is famous for its barbecue. But, good barbecue comes at a cost: Pit masters have to bear the costs of producing slow-
roasted pulled pork and beef briskets. There is also an external cost: Every time a pit master roasts another rack of ribs, it offends the sensibilities of nearby animal lovers. Consider the graphical representation below of a typical pit master in the competitive barbecue industry: 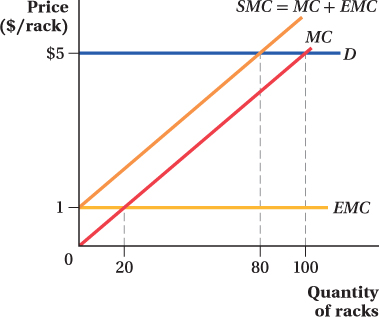
What is the market price of barbecue?
The market price is $5, where marginal benefit equals marginal cost.
How much psychic damage (external cost) do animal lovers suffer for each rack roasted?
The external cost is $1 regardless of the number of racks roasted.
If our pit master accounts only for her private costs, how many racks will she roast? How much total damage will animal lovers suffer?
The intersection of the marginal benefit curve (demand) and the marginal cost curve determines the number of racks. Thus, 100 racks will be roasted. Animal lovers will suffer damage of $1 for each rack, for a total damage of $100.
If our pit master feels sympathy for animal lovers and wholly considers their feelings in her decision about how many racks to produce, how many racks will she roast?
Incorporating the external costs would lead the pit master to produce 80 racks.
Does the decision to consider animal lovers’ feelings eliminate the damage they suffer from transactions in the rib market?
The total damage suffered by animal lovers will be $80. Some of the damage is eliminated, but not all.
Cutting output below the level you determined in (d) clearly benefits animal lovers. Who is hurt by such a decision? Explain why such an output cut would not be Pareto efficient, that is, there is another allocation that would make someone better off without making anyone worse off.
Cutting the level of output further would hurt the pit master, who would be foregoing profits. Such a cut is not Pareto optimal, because although the output cut would reduce damage to the animal lovers by $1 per rack roasted, below 80 units any output cut will cost the pit master more than $1 in lost profit.
Jill sells bouquets of flowers that she grows in her backyard. Jill’s marginal cost of producing bouquets is given by MC = 0.25Q, where Q is the number of bouquets she makes. Jill can sell all the bouquets she wishes at the local farmers’ market for $6 per bouquet. Unfortunately, Jill’s floriculture aggravates the allergies of her next-
door neighbor, Cooper: Every bouquet that Jill grows produces 50 cents’ worth of sneezes. Jill wants to maximize her profit. Determine the profit-
maximizing quantity of bouquets. Assume that Jill produces the quantity of bouquets you determined in (a). Add up the cost of the last bouquet to Jill and the cost that bouquet imposes on Cooper, and compare your answer to the $6 worth of benefit the last bouquet creates for the buyer. Is producing the last bouquet a good thing for society?
From society’s standpoint, is Jill overproducing or underproducing bouquets?
Suppose that Jill marries Cooper. Determine the social marginal cost of producing bouquets by adding the 50 cents’ worth of damage each bouquet causes Cooper to Jill’s private marginal cost. Express your answer as an equation.
Determine how many bouquets Jill should produce if she fully considers the costs she imposes on her new husband. Explain why it makes a difference if Cooper is just a neighbor or is Jill’s husband.
Suppose that the inverse demand for marching band music is given by P = $1,000 – Q. Because marching bands across the world produce music of sufficient quality at increasing marginal cost, the industry marginal cost is given by MC = 0.75Q. Unfortunately, marching band music is not produced in a vacuum: People near marching bands become increasingly aggravated the more music they hear. At the industry level, the external marginal cost is given by EMC = 0.25Q.
686
Graph the demand, marginal cost, and external marginal cost functions.
If marching bands do not consider the external marginal costs they impose on others, how many songs will be played?
Calculate the total consumer surplus.
Calculate the total producer surplus.
Calculate the total surplus to market participants.
Calculate the total damage to those harmed. (Hint: This damage can be represented as the area under the EMC curve. It’s up to you to figure out why!)
Subtract the damage to those harmed from total surplus to market participants to determine the net value created for society by marching band music.
Determine social marginal cost.
Determine the quantity of marching band music that would be produced if marching bands were forced to consider the costs they imposed on others.
What happens to the price of marching band music if the bands were forced to consider the external marginal costs?
As you did in (b), calculate consumer surplus, producer surplus, and total damage. (Be sure to remember that producer surplus is the area between private marginal cost and the price!) Compared to your answers in (b),
What happens to the total surplus received by market participants when external marginal costs are considered?
What happens to the damage created by marching band music?
What happens to the net value created for society by marching band music?
Gasoline brings great benefit to those who buy it, but burning it also creates external costs. Consider the following graph, which shows the demand for gasoline, the private marginal cost of producing gasoline, and the social marginal cost of producing gasoline.
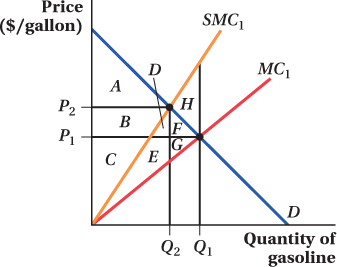
Suppose that buyers and producers of gasoline do not consider the external marginal costs they impose on others. Determine the equilibrium quantity and price; then use the letters in the diagram to fill in the appropriate spaces in the table below:
External Marginal Costs Not Considered External Marginal Costs Considered Consumer Surplus Producer Surplus External Damage (–) Total net value to society The equilibrium price is P1 and quantity is Q1
External Marginal Costs Not Considered External Marginal Costs Considered Consumer Surplus A + B + D + F Producer Surplus C + E + G External Damage (−) D + E + F + G + H Total net value to society A + B + C – H Suppose that conscientious sellers, out of the sheer goodness of their hearts, decide to incorporate external marginal costs into their production decisions. Determine the new quantity (Hint: Use the social marginal cost curve) and price, then use the letters in the diagram to fill in the appropriate spaces in the table above. (Be sure to remember that producer surplus is the area above private marginal cost and below the price, out to the relevant quantity.)
The equilibrium price is P1 and quantity is Q1
External Marginal Costs Not Considered External Marginal Costs Considered Consumer Surplus A + B + D + F Producer Surplus C + E + G External Damage (−) D + E + F + G + H Total net value to society A + B + C – H Producers rarely do something out of the goodness of their hearts, and are likely to consider only their private marginal costs. Compare total surplus in both cases to determine the deadweight loss of the externality when external marginal costs are not considered.
As indicated in the table above, when external costs are ignored by producers, total net value is lower by area H. Thus, H is the deadweight loss.
The private demand for drive-
in movies is given by P = 20 – 0.1Q. The industry marginal cost of showing drive- in movies is given by MC = 0.1Q. Graph the private demand and marginal cost curves, and determine the price and quantity of movies that will be shown.
Drive-
in movies can be viewed imperfectly from outside the fence. The external marginal benefits received by such viewers are given by EMB = 2 – 0.01Q. Graph the external marginal benefit curve, and then use that information to graph the social demand curve. Suppose that all drive-
in movies are nationalized and shown for the public good. The Movie Czar chooses the price and quantity of movies that bring the greatest benefit net of costs to all viewers, regardless of the vantage point from which they view the movie. Determine the optimal price and quantity of drive- in movies. Indicate the deadweight loss created by the positive externality as an area on your graph, and calculate its value. (Hint: You’ll need to determine how much external marginal benefit the very last unit of output created when drive-
ins were privately run.) Can government-
run movies potentially improve on the private market outcome when a positive externality exists?
687
Suppose that growing flowers produces both a positive externality (people in the neighborhood get to view the flowers) and a negative externality (the flowers aggravate peoples’ allergies).
True or false, and explain your answer (using a diagram): We can say for sure that too many flowers are being produced.
True or false, and explain your answer (using a diagram): We can say for sure that the market price of flowers is too high.
The inverse demand for leather is given by P = 50 – 0.5Q. The industry supply of leather is determined by its marginal cost: MC = 0.45Q. Unfortunately, the production of leather causes noxious chemical residue to leach into groundwater supplies. The external marginal cost caused by these residues grows with the amount of output, and is measured as EMC = 0.05Q.
Suppose that the government wishes to reduce the externality to efficient levels by imposing a restriction on quantity (a quota). What maximum level of output should it set for leather production? What price would prevail in the marketplace once this quota is in place?
The SMC is MC + EMC = 0.45Q + 0.05Q = 0.5Q. The efficient output level can be found where MB = SMC:
50 – 0.5Q = 0.5Q
Q* = 50
Thus, government should set the quota at 50 units. The price that prevails in the marketplace once this quota is in place is
P = 50 – 0.5Q* = 50 – 0.5 × 50 = $25
Suppose that the government wishes to reduce the externality to efficient levels by levying a tax on leather production. How high would that tax need to be? What is the resulting net price paid by buyers once the tax is in place? How much leather is bought and sold with the tax in place?
At the efficient level of production, Q*= 50, the external damage can be calculated as 0.05Q, or $2.50. If government imposes a $2.50 tax on producers, their private marginal costs will be given as
MC = 0.45Q + 2.50
Producers will find the profit-
maximizing level of output where MB = MC, or where 50 – 0.5Q = 0.45Q + 2.50
Solving, we get 50 units for Q, the profit-
maximizing level of output. The prevailing market price can be found by substituting Q = 50 into the MB curve: P = 50 – 0.5(50) = $25
Buyers will pay $25. Sellers will receive that amount less the tax, or $22.50.
Consider the market for smelted kryptonite depicted below. A by-
product of kryptonite smelting is the release of clouds of toxic blackish- yellow smoke. Each ton of toxic smoke emitted causes nearby residents’ health- care expenditures to rise; the external marginal costs associated with the toxic exhaust are depicted as EMC on the graph below: 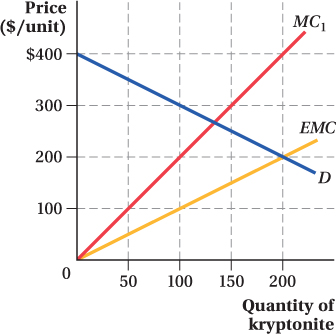
On the diagram, carefully graph the social marginal cost curve associated with the kryptonite industry. Precision matters!
Without any environmental regulation, how much kryptonite is produced?
From society’s standpoint, how much kryptonite should be produced?
Regulators can achieve the efficient level of kryptonite production by imposing a tax on kryptonite production. To achieve the efficient level of production, how big should that tax be?
Draw an industry supply curve that reflects the tax you determined in part (d). Show that private producers, forced to internalize their externality by the tax, produce the socially optimal amount.
Could the same result have been achieved by assessing a tax on the buyers of kryptonite? If so, how much would that tax need to be?
In Paris, hundreds of small bakeries produce bread for sale to their customers at a marginal cost of MC = 2 + 0.1Q. The inverse demand for bread is given by P = 10 – 0.1Q, where P is in euros per loaf and Q is loaves per hour. The baking of bread also creates a positive externality: There is nothing quite like the smell of fresh-
baked bread. Tourists and residents receive external marginal benefits given by EMB = 2 – 0.02Q. Find the quantity of bread produced in Paris in the absence of any government intervention.
Without any government intervention, the quantity of bread produced is
P = 10 – 0.1Q = 2 + 0.1Q = MC
0.2Q = 8
Q = 40
To achieve the socially optimal output, government can use a price-
based intervention. Determine the ideal measure for government to use to achieve this goal. Specify both the type of policy and its magnitude. Ideally, society would like producers to consider all of the benefits their activity creates, both internal and external. Thus, the total social benefit is given as
SD = P + EMB = 10 – 0.1Q + 2 – 0.02Q
= 12 – 0.12Q
SB-
30 So, the magnitude of a price-
based intervention is 12 – 0.12Q = 2 + 0.1Q = MC
0.22Q = 10
Q ≈ 45.45
Producers are under-
producing relative to the welfare- maximizing quantity of 45.45. The government can use a price- based intervention to encourage them to produce more. In this case, the appropriate intervention is to subsidize production. At the ideal quantity, bread baking creates an external marginal benefit of EMB = 2 – 0.02(45.45) = $1.09
If the government offers producers a subsidy of $1.09 per loaf, producers’ marginal cost becomes
MC = 2 + 0.1Q – 1.09
Equating MC and MB yields
2 + 0.1Q – 1.09 = 10 – 0.1Q
Q = 45.45
A subsidy of $1.09 encourages producers to produce the socially optimal amount.
688
Consider the diagram below, which depicts the external marginal cost of pollution by each ton of sulfur dioxide emitted by power plants, and the marginal abatement cost of eliminating that pollution.

Explain why the marginal abatement cost (or marginal benefit of pollution) curve slopes downward.
Find the efficient level of pollution and indicate it on your graph.
Firms, which care little about the damage imposed on people hundreds or thousands of miles away, have little incentive to produce the optimal amount of pollution on their own. Explain how, if regulators tax the producer $400 for each ton of pollutant emitted, power producers will have an incentive to cut emissions to exactly the socially optimal level.
Explain why a tax of $600 for each ton of pollutant emitted is too high a tax, and $200 per ton is too low a tax.
Brimstone is a caustic by-
product of the production of fairy dust. The external marginal cost caused by inhalers of brimstone is indicated in the graph at right as MCP. The marginal abatement costs to fairy dust producers (MBP = MAC) are indicated as well. Suppose that regulators overestimate the damage that brimstone causes; their best guess of the harm is shown as MCPe. 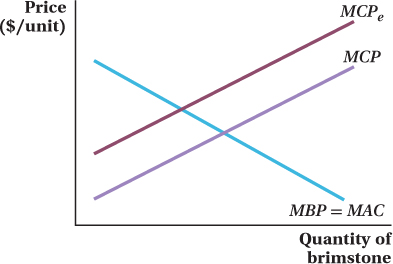
Show (graphically) that if regulators attempt to achieve what they believe to be an efficient amount of brimstone, it doesn’t matter whether they attempt to limit the quantity of brimstone, or set what they believe to be an efficient tax.
Show graphically that the elasticities of the marginal abatement cost and marginal cost of pollution are irrelevant in this special case to the choice of a quantity or price intervention.
Show that the results you demonstrated in (a) and (b) also hold if regulators underestimate the amount of marginal pollution cost brimstone causes.
Al regularly rehearses accordion music on his back deck with members of his musical troupe, the Starland Polka Band. Practicing on his deck saves him the $500 per year it would take to rent a rehearsal space. Unfortunately, practicing on his deck keeps his neighbor, Marcy, awake at night. The value of Marcy’s lost sleep is $600 per year.
Is it efficient for Al to rehearse on his back deck? Explain your answer.
No. Rehearsing on the deck brings Al $500 of benefits, but costs Marcy $600 in lost sleep. Society loses $100 of welfare as a result of Al’s rehearsals.
If the law says that it is illegal for Al to rehearse on his back deck, will Al end up practicing there? What might Marcy do to try to stop him?
If rehearsals are illegal, Marcy can simply call the police to put an end to Al’s rehearsals. No rehearsals will take place.
Suppose that the law says it is legal for Al to rehearse on his back deck.
How much is Marcy willing to pay to get him to stop?
Marcy is willing to pay Al up to $600 per year to rehearse elsewhere.
What is the minimum amount of money Al is willing to accept in exchange for his silence?
The minimum amount of money that Al is willing to accept is $500.
If possible, craft a bargain between Marcy and Al that results in his silence. Show that the bargain (if possible) makes both parties better off.
Let us assume that Marcy pays Al $550 for silence. Al is better off taking the offer, as he gains $50 (= $550 – $500) and Marcy is better off paying him as $600 – $550 = $50.
Given your answers to (b) and (c), does the outcome of this conflict depend on the law? Is the outcome consistent with your answer to (a)?
689
The outcome does not depend on the law. When rehearsing is illegal, Marcy calls the police. When rehearsing is legal, Marcy pays Al to rehearse elsewhere. No matter what the law states, society gets the same efficient outcome.
Suppose that instead of doing $600 damage to one neighbor, Al does $1 damage to 600 neighbors. Are those 600 neighbors as likely to be able to convince him to stop as easily as Marcy can? Explain.
It will be more difficult for the neighbors to organize and to gather the amount that would compensate Al for the rent. Neighbors will try to avoid chipping in and free-
ride. Thus, even though it is not efficient for Al to rehearse on his back deck, that may be the outcome for society.
Assume that everyone agrees that global warming is both real and caused by humans. Give two major reasons why bargaining in the spirit of Coase is unlikely to resolve the problem of excess carbon emissions.
Two dairy farmers, Ben and Jerry, share a common pasture. Each has a choice of grazing 1 or 2 cows on the pasture. If 2 cows graze on the pasture, each will give 1,000 gallons of milk each year, which may be sold for $1 each at the local farmers’ market. If 3 cows graze on the pasture, the grass will be thinner and each will give 750 gallons of milk. If 4 cows graze on the pasture, the grass will have little chance to recover and each cow will only give 400 gallons of milk.
What is the efficient number of cows to keep on the common pasture—
2, 3, or 4? Explain. Number of cows 2 3 4 Total gallons of milk each year 2,000 2,250 1,600 The efficient number of cows is 3.
If Jerry keeps 1 cow in the pasture, how many should Ben keep? (Assume that the only thing that concerns Ben is revenue received at the farmers’ market.)
If Ben keeps 1 cow, that cow will produce 1,000 gallons of milk and Ben will earn $1,000. If Ben keeps 2 cows, each will produce 750 gallons of milk and Ben will earn $1,500. Ben will keep 2 cows.
If Jerry keeps 2 cows in the pasture, how many should Ben keep?
If Ben keeps 1 cow, that cow will produce 750 gallons of milk and Ben will earn $750. If Ben keeps 2 cows, each will produce 400 gallons of milk and Ben will earn $800. Ben will keep 2 cows.
Repeat your analysis for Jerry. What outcome are we likely to see—
2, 3, or 4 cows in the pasture? Following similar reasoning, Jerry’s best choice is to keep 2 cows regardless of how many cows Ben grazes. So, both Ben and Jerry will keep 2 cows on the pasture. Relative to what is socially ideal (3 cows), Ben and Jerry keep too many cows and the pasture is overgrazed.
What strategies might be useful in preventing overgrazing on the commons?
It could be useful to restrict the number of cattle grazed on some specific area or to charge a tax for grazing. An alternative would be to sell the pasture to Ben or Jerry, who will then have a private incentive to graze the socially ideal number of cows.
Classify each of the following goods using these terms: nonrival, nonexcludable, private good, club good, public good, and common resource.
Hamburger
Lighthouse
Flood control
Swimming pool
Park
Broadcast television
Cellular telephone service
Computer software
Using the appropriate terminology, explain why public radio stations, which rely on contributions from listeners, always seem to be in financial jeopardy.
A home-
team baseball victory produces benefits for residents (in terms of hometown pride) that is both nonrival and nonexcludable. The graph below depicts the marginal benefits that Beatrice, Edward, and Charlotte (the residents of a very tiny town indeed) receive from home- team wins. The graph also depicts the marginal costs of achieving each victory. 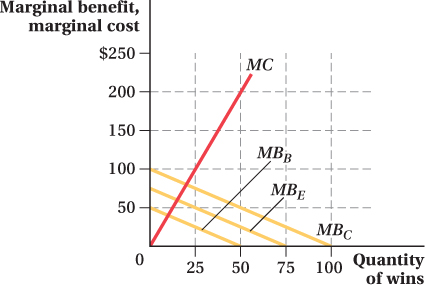
Draw the total marginal benefit received by hometown residents. Graph your result carefully.
Determine the socially optimal number of wins. Indicate this amount on your graph.
There are two consumers of mosquito abatement, a public good. Dash’s benefit from mosquito abatement is given by MBD = 100 – Q, where Q is the quantity of mosquito abatement. Lilly’s benefit is given by MBL = 60 – Q.
Calculate the total marginal benefit, MBT.
Suppose that mosquito abatement can be provided at a marginal cost of MC = 2Q. Find the optimal level of mosquito abatement.
How much benefit do Dash and Lilly enjoy at the optimal level of mosquito abatement? (Assume Dash and Lilly do not have to bear any of the cost personally, but that abatement is provided by the government at no direct cost to the recipient.)