As we saw in the chapter, utility maximization—where you take income as given and find the combination of goods that will give you the greatest utility—is only one way to look at the consumer’s optimization problem. Another is expenditure minimization, in which you start with a level of utility and find the cheapest bundle that achieves that utility level. In many ways, expenditure minimization is less intuitive—in real life, you probably do face a set income, but no contract you sign will ever specify your utility. But, ultimately, expenditure minimization leads to the same answer. What is more, the expenditure-minimization technique is extremely useful in the appendices for Chapter 5, Chapter 6 and Chapter 7. In particular, this technique makes a lot more sense in the context of the producer’s cost-minimization problem in Chapter 7.

Let’s demonstrate the equivalence of utility maximization and expenditure minimization using Antonio’s utility function from the Figure It Out in the chapter and the Lagrangian method (the first approach is identical to that for utility maximization except that you plug into the utility constraint instead of the budget constraint in the last step). We write out Antonio’s expenditure-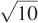minimization problem given a constant utility of or 10^0.5, the utility at his optimal consumption bundle from the utility-maximization problem above:

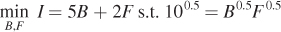
or

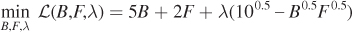
153

As before, solve for the first-order conditions:

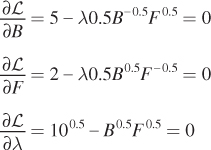
Then solve for λ in the first two conditions:

λ0.5B^–0.5F^0.5 = 5

λ = 10B^0.5F^–0.5

λ0.5B^0.5F^–0.5 = 2

λ = 4B^–0.5F^0.5

Set the two expressions for λ equal to each other and solve for F as a function of B:

λ = 4B^–0.5F^0.5 = 10B^0.5F^–0.5

4F^0.5F^0.5 = 10B^0.5B^0.5

F = 2.5B

Now substitute F as a function of B into the utility constraint:

10^0.5 = B^0.5F^0.5 = B^0.5(2.5B)^0.5 = (2.5)^0.5B^0.5B^0.5

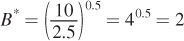
F^* = 2.5B^* = 2.5(2) = 5

This optimal bundle of goods costs Antonio

5B* + 2F^* = 5(2) + 2(5) = $20

the minimum expenditure needed to achieve 10^0.5 units of utility.

Expenditure minimization is a good check of our cost-minimization problem because it should yield the same results. In this case, as with utility maximization, Antonio purchases 2 burgers and 5 orders of fries for a cost of $20 and a total utility of 10^0.5.