Consumers’ preferences underlie every decision they make. Economists think of consumers as making rational choices about what they like best, given the constraints they face.

Consumers make many choices every day about what to buy and what not to buy. These choices involve many different goods: Buy a giant bag of Twizzlers and walk home, or buy a bus ticket and leave a sweet tooth unsatisfied? Buy a new video game or buy a new water pump for the car? Buy a ticket to the ball game or go to a bar for drinks with friends and watch the game on TV? To understand how consumers form their preferences for thousands of goods and services, we need to make some simplifying assumptions. Specifically, we assume that all decisions about what to buy share four properties that help consumers determine their preferences about all the possible combinations of goods and services they can buy.

Given these assumptions about preferences, we could create a list of all the consumer’s preferences between any possible bundles for every decision. But because such a list would include billions of possible bundles, it would be basically useless as a decision aid.

Instead, economists use the concept of utility and a mathematical description called a utility function to describe preferences more simply. Utility describes how satisfied a consumer is. For practical purposes, you can think of utility as a fancy word for happiness or well-being. It is important to realize that utility is not a measure of how rich a consumer is. Income may affect utility, but it is just one of many factors that do so.

A utility function summarizes the relationship between what consumers consume and their level of well-being. A function is a mathematical relationship that links a set of inputs to an output. For instance, if you combine the inputs eggs, flour, sugar, vanilla, butter, frosting, and candles in just the right way, you end up with the output of a birthday cake. In consumer behavior, the inputs to a utility function are the different things that can give a person utility. Examples of inputs to the utility function include traditional goods and services like cars, candy bars, health club memberships, and airplane rides. But there are many other types of inputs to utility as well, including scenic views, a good night’s sleep, spending time with friends, and the pleasure that comes from giving to charity. The output of the utility function is the consumer’s utility level. By mapping the bundles a consumer considers to measures of the consumer’s level of well-being—this bundle provides so much utility, that bundle provides so much utility, and so on—a utility function gives us a concise way to rank a consumer’s bundles.

Utility functions can take a variety of mathematical forms. Let’s look at the utility someone enjoys from consuming Junior Mints and Kit Kats. Generically, we can write this utility level as U = U(J, K), where U(J, K) is the utility function and J and K are, respectively, the number of Junior Mints and Kit Kats the consumer eats. An example of a specific utility function for this consumer is U = J × K. In this case, utility equals the product of the number of Junior Mints and Kit Kats she eats. But it could instead be that the consumer’s utility equals the total number of Junior Mints and Kit Kats eaten. In that case, the utility function is U = J + K. Yet another possibility is that the consumer’s utility is given by U = J^0.7K^0.3. Because the exponent on Junior Mints (0.7) is larger than that on Kit Kats (0.3), this utility function implies that a given percentage increase in Junior Mints consumed will raise utility more than the same percentage increase in Kit Kats.

108

These are just a few examples from the large variety of possible utility functions we could imagine consumers having for these or any other combination of goods. At this point in our analysis of consumer behavior, we don’t have to be too restrictive about the form any particular utility function takes. Because utility functions are used to represent preferences, however, they have to conform to our four assumptions about preferences (rankability and completeness, more is better, transitivity, and variety is important).

One of the most important concepts related to utility functions is marginal utility, the extra utility a consumer receives from a 1-unit increase in consumption.3 Each good in a utility function has its own marginal utility. Using the Junior Mints and Kit Kats utility function, for example, the marginal utility of Junior Mints, MU_J, would be

3 Marginal utility can be calculated for any given utility function.

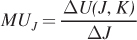
where ΔJ is the small (1-unit) change in the number of Junior Mints the consumer eats and ΔU(J, K) is the change in utility she gets from doing so. Likewise, the marginal utility of consuming Kit Kats is given by

Later in this chapter, we see that marginal utility is the key to understanding the consumption choices a person makes.

One important point about utility and the four preference assumptions we started with is that they allow us to rank all bundles of goods for a particular consumer, but they do not allow us to determine how much more a consumer likes one bundle than another. In mathematical terms, we have an ordinal ranking of bundles (we can line them up from best to worst), but not a cardinal ranking (which would allow us to say by exactly how much a consumer prefers one bundle to another). The reason for this is that the units in which we measure utility are essentially arbitrary.

An example will make this clearer. Let’s say we define a unit of measurement for utility that we call a “util.” And let’s say we have three bundles: A, B, and C, and a consumer who likes bundle A the most and bundle C the least. We might then assign these three bundles values of 8, 7, and 6 utils, respectively. The difficulty is that we just as easily could have assigned the bundles values of 8, 7, and 2 utils (or 19, 17, and 16 utils; or 67, 64, and 62 utils, etc.) and this would still perfectly describe the situation. You can say that you like something better, but how can you describe how happy it makes you, objectively? There is no real-world unit of measurement like dollars, grams, or inches with which to measure utility, so we can shift, stretch, or squeeze a utility function without altering any of its observable implications, as long as we don’t change the ordering of preferences over bundles.4

4 In mathematical parlance, these order-preserving shifts, squeezes, or stretches of a utility function are called monotonic transformations. Any monotonic transformation of a utility function will imply exactly the same preferences for the consumer as the original utility function. Consider our first example of a utility function from consuming Junior Mints and Kit Kats, U = J × K. Suppose that it were U = 8J × K + 12 instead. For any possible bundle of Junior Mints and Kit Kats, this new utility function will imply the same ordering of the consumer’s utility levels as would the old function. (You can put in a few specific numbers to test this.) Because the consumer’s relative preferences don’t change, she will make the same decisions on how much of each good to consume with either utility function.

109

It often doesn’t really matter that we have only an ordinal ranking of utility. We can still provide answers to the important questions about how consumers behave and how this behavior results in a downward-sloping demand curve.

One set of questions we will not be able to answer, though, are questions that make interpersonal comparisons, meaning comparisons of one consumer’s utility to another’s. We can say that if one person prefers Concert A tickets to Concert B tickets and the other person prefers the reverse, then both will be better off if the first person gets the A tickets and the second person gets the Bs. But if they both prefer A, we have no easy way to tell who would be better off getting the A tickets. (These types of questions relate to the area known as welfare economics, which we discuss in several places later in the book. For now, however, we focus on the preferences of one consumer at a time.)

Just as important as the assumptions we make when analyzing utility functions are the assumptions that we do not make. For one, we do not impose particular preferences on consumers. An individual is free to prefer dogs or ferrets as pets, just as long as they follow the four preference assumptions. We don’t make value judgments about what consumers should or shouldn’t prefer. Even if it is Justin Bieber music, preferences are just a description of how a person feels. We also don’t require that preferences remain constant over time. Someone may prefer sleeping to seeing a movie tonight, but tomorrow prefer the opposite.

The concepts of utility and utility functions are general enough to account for a consumer’s preferences over any number of goods and the various bundles into which they can be combined. As we proceed in building our model of consumer behavior, however, we focus on a simple model in which a consumer buys a bundle with only two goods. This approach is an easy way to see how things work, and the ideas still apply in the more complicated situations.