Economists use the term returns to scale to describe what happens to the amount of output in response to a proportional increase in all of the inputs.

A production function has constant returns to scale if changing the amount of capital and labor by some multiple changes the quantity of output by exactly the same multiple. (For example, doubling capital and doubling labor results in a doubling of output.) Our Cobb–Douglas production function Q = K^0.5L^0.5 has constant returns to scale. This is apparent in Table 6.2. Output (Q) is 1 when L = 1 and K = 1. If you double both of them to L = K = 2, output doubles, too: Q = 2. If you double labor and capital again to L = K = 4, then Q = 4.

A production function has increasing returns to scale if changing all inputs by some multiple changes output more than proportionately. (Doubling capital and labor more than doubles output.) Decreasing returns to scale exist if adjusting all inputs by the same multiple changes output by less than that multiple. (Output does not fully double when inputs are doubled.)

We assumed earlier in the chapter that inputs have diminishing returns—their marginal products fall as firms use more of them. So, how can returns to scale be constant or increasing when there are diminishing returns to inputs? The key difference between the two concepts is that marginal products refer to changes in only one input while holding the other input constant, but returns to scale is about changes in all inputs at the same time. In other words, diminishing marginal returns refers to short-run changes, while returns to scale is a long-run phenomenon because we are changing all inputs simultaneously.

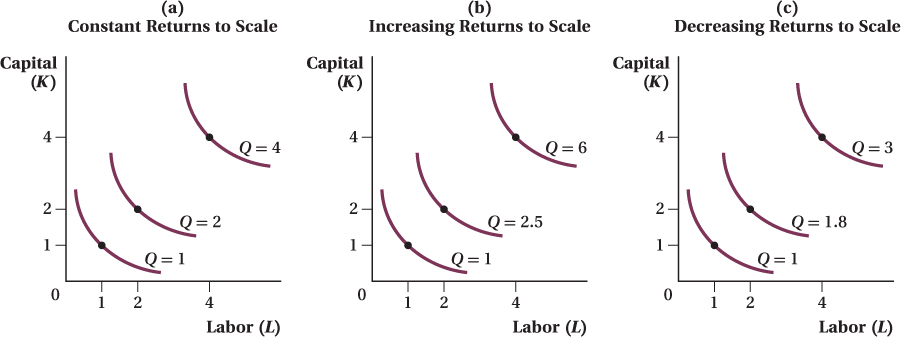
Figure 6.12 demonstrates these returns to scale cases using isoquants. In the first panel, a doubling of inputs leads to the doubling of outputs, so the technology exhibits constant returns to scale. Similarly, the isoquants in panel b indicate increasing returns to scale, while decreasing returns to scale are shown in panel c.

224

A number of aspects of a production technology determine a production function’s returns to scale.

In some ways, it is natural for a production function to have constant returns to scale. If a firm can replicate a production process, output should grow proportionately with inputs. A company with a factory that makes 1,000 cars a day using 3,000 units of labor and 4,000 units of capital could build an identical factory across the street and have identical output. Double all of its inputs, and it doubles its output. Adding a third identical factory and set of workers should again increase output commensurately, and so on.

But there are other influences that can push production functions toward increasing or decreasing returns to scale as well. For example, a common source of increasing returns to scale is fixed costs, payments to inputs that must be used no matter what the output quantity is, even if it is zero. (We talk more about fixed costs in Chapter 7.) If the firm must use a certain quantity of inputs before it produces anything, increasing inputs after these fixed costs are paid will increase output more than proportionately. Consider the example of a firm that uses three inputs to earn its revenues: capital, labor, and a Web page. We assume the Web page input is a fixed cost, because the cost of its upkeep is basically the same whether the firm makes a lot of product or just a little. If the firm doubles its capital and labor inputs while keeping the same Web page, it will probably double its output. Because the firm is able to double its output without having to double all its inputs, it exhibits increasing returns to scale.

225

A firm can also experience increasing returns to scale if there is learning by doing. As a company makes more of a good, it tends to become more and more efficient at production. If a firm gets better at producing as it produces more output, then it may be able to produce the second batch of output using fewer resources than it required for the first batch. That is, it will be able to double its output without having to double its inputs.

226

Decreasing returns to scale are possible but should be unlikely in the long run for the same reason that constant returns to scale are natural. If inputs are measured properly, and the firm has ample time to adjust all its inputs, the firm can just replicate its current production operation, allowing it to increase output by the same factor as inputs. Nevertheless, economists sometimes measure firms’ production functions and find that they exhibit decreasing returns to scale. Most often, such a finding indicates that not all inputs are being fully measured. For instance, suppose a company builds a seemingly identical second factory with the same number of workers and capital as its first one, yet the second is less efficient. This might be because the second factory’s manager is not as talented as the manager at the first, or because the company’s productive corporate culture isn’t as well established as at the original factory. Managerial talent and corporate culture are inputs to the firm’s production, but are often too difficult to measure to include in standard labor and capital inputs measures. To have true decreasing returns to scale, the second factory would have to be less efficient even if the managerial talent and corporate culture were at the same level as at the first factory.