Problems
Jing is considering starting a new business selling organic groceries. It would cost her $350,000 a year to rent store space and buy the groceries from a wholesaler, and she would have to quit her current job and give up a $70,000 annual salary.
What is Jing’s opportunity cost of starting the business?
If Jing can make an accounting profit of $50,000 a year selling the organic groceries, should she start the business?
Indicate whether the following statements are true or false, and then briefly explain your reasoning.
It is possible for accounting and economic costs to be equal, but it is never possible for economic costs to be less than accounting costs.
True. Economic costs include both, accounting costs and the opportunity cost. Conditional on the opportunity cost equaling zero, accounting and economic costs may be equal, but since the opportunity cost cannot be negative, the economic costs are at least as high as the accounting costs.
It is possible for a firm to show an economic profit without showing an accounting profit.
No, it is not possible. The economic profit is the total revenue minus the economic cost, whereas the accounting profit is the total revenue minus the accounting costs. Since economic cost is at least as large as the accounting cost, it is not possible to make an economic profit without making an accounting profit.
Philo T. Farmsworth is a corn farmer with a 40-
acre tract of land. Each acre can produce 100 bushels of corn. The cost of planting the tract in corn is $20,000, and the cost of harvesting the corn is $10,000. In May, when corn is selling for $10 per bushel, Philo plants his crop. In September the price of corn has fallen to $2 per bushel. What should Philo do? Explain, assuming that there are no costs involved with bringing the corn to market to sell. Each year on January 1, millions of Americans, having made New Year’s resolutions to lose weight and get in shape, purchase annual gym memberships. A CNN survey recently suggested that nearly 30% of all New Year’s resolutions are abandoned by February 1; 80% by July. In other words, millions of people buy expensive gym memberships and then fail to use them. Does this indicate that they fell victim to the sunk cost fallacy? Or does it indicate that they understand the nature of sunk costs very well? Explain your answer.
True or false: All sunk costs are fixed, but not all fixed costs are sunk. Explain your response.
Karam recently opened a bar & grill. The costs associated with his new business are as follows:
$300,000 to build the restaurant
$30,000 for a liquor license
$50,000 on furniture and kitchenware
2 cooks who will each be paid $5,000 per month
5 waiters who will each be paid $3 per hour plus tips
Which of Karam’s costs are fixed, and which are variable? Explain.
Amanda owns a toy manufacturing plant with the production function Q = 100L – 3,000, where L is hired labor hours. Assume that Amanda has no fixed costs.
Rearrange Amanda’s production function to show how many workers Amanda would have to hire to produce a given level of output. In other words, isolate L on the left-
hand side, expressing L as a function of q. Begin by putting L on the left-
hand side: 100L = 3000 + Q
L = 30 + 0.01Q
Because Amanda has no fixed costs, all of her costs derive from paying workers. In other words, TC = w × L. Substitute your answer from (a) into this equation to find Amanda’s total cost function.
TC = w (30 + 0.01Q) = 30w + 0.01Qw
-
A Toyota Camry costs $19,600 and has an average gas mileage of 27 mpg. A Toyota Prius costs $23,000 and has an average gas mileage of 50 mpg. Assuming gas costs $4 per gallon, generate total cost equations as a function of miles driven for each of these cars and identify the fixed and variable costs. How many miles do you have to drive before the two cars have the same total cost?
Consider the costs for Gisela’s cupcake business:
Quantity (batches) Fixed Cost ($) Total Cost ($) 1 50 75 2 50 85 3 50 102 4 50 127 5 50 165 6 50 210 Re-
create the above table with columns showing Gisela’s variable cost, average total cost, average fixed cost, and average variable cost. Q (batches) Variable Cost ($) Average Total Cost ($) Average Fixed Cost ($) Average Variable Cost ($) 1 25 75 50 25 2 35 42.5 25 17.5 3 52 34 16.67 17.33 4 77 31.75 12.5 19.25 5 115 33 10 23 6 160 35 8.33 26.67 Daniel’s Midland Archers (DMA) makes children’s wooden practice arrows. Draw a set of representative short-
run cost curves for DMA. Include average variable cost, average fixed cost, average total cost, and marginal cost. Suppose that Congress imposes a 39-
cent excise tax on each children’s wooden practice arrow DMA sells. Illustrate the effects of this tax on the cost curves of DMA. Which curves shift and which do not? Suppose that the city where DMA produces arrows increases the annual property tax on DMA’s factory from $80,000 to $150,000. Illustrate the effects of this tax on the cost curves of DMA. Which curves shift and which do not?
279
-
Derive formulas for average fixed cost, average variable cost, average total cost, and marginal cost for the following cost function:
TC = 100 + 10Q
You are the CEO of a major producer of funnel cakes. Your cost accountant has provided you with a table describing your cost structure, but you have inadvertently dripped cooking grease on it and most of the table is illegible. Reconstruct the table below, given the remaining legible numbers:
Q TC FC VC MC AVC AFC ATC 0 — — — — 1 17 2 15 3 101 4 14.5 5 122 67 11 6 21 True or false: Average variable cost reaches its minimum point at a lower level of output than average total costs. Explain your answer, using a graph of average and marginal costs to illustrate.
-
Suppose a firm has the following production function: Q = 2KL. The marginal product of capital for this production function is 2L, and the marginal product of labor is 2K. If capital rents for $100 per unit per day, labor can be hired for $200 per unit per day, and the firm is minimizing costs,
Find the total cost of producing 60 units of output.
Suppose you want to determine the cost of producing the more general q units of output. Using the same set of procedures you followed in (a), but a more general q instead of 60, find this firm’s total cost function, which expresses total cost as a function of q.
Divide the total cost function you found in (b) by q to determine this firm’s average cost function.
You run a specialty bicycle company, which produces a limited quantity of extremely tricked out racing bikes. Consider the following graph, which illustrates the short-
run average total cost curves corresponding to three possible plant sizes: small, medium, and large. 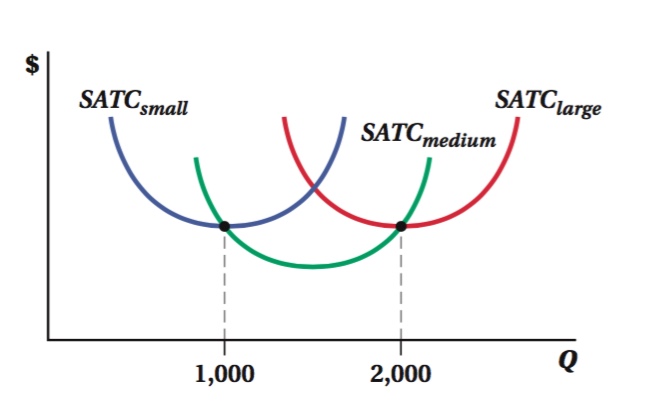
If you wanted to produce 900 bikes, which plant size should you choose, and why? What if you wanted to produce 1,100 instead?
If you wanted to produce 2,100 bikes, which plant size should you choose, and why? What if you wanted to produce just 1,900?
Darken the long-
run average total cost curve your specialty bicycle company faces.
Suppose an increase in the minimum wage alters the cost of producing fast-
food hamburgers. Show what happens to McDonald’s long- run expansion path as a result of this wage increase. Since labor becomes more expensive, the isocost lines will rotate clockwise (and therefore become steeper).
The long-
run expansion path (which shows points of tangency between isocost lines and isoquants) shifts up as a result of the wage increase. The optimal production would employ more capital and less labor. 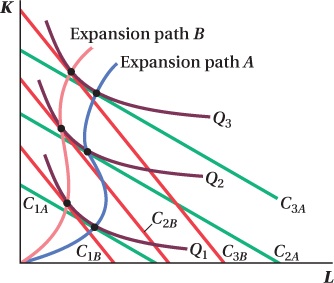
-
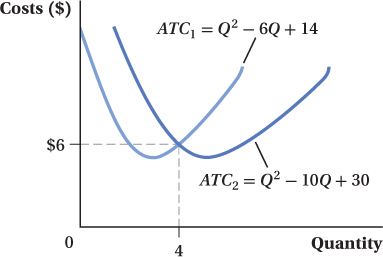
A builder of custom motorcycles has a choice of operating out of one garage or two. When it operates out of one garage, its average total cost of production is given by ATC1 = Q2 – 6Q + 14. If it operates out of two garages, its average total cost of production is given by ATC2 = Q2 – 10Q + 30. What does this firm’s LATC look like? Can you describe it as a function?
A builder will be indifferent between the two choices when
ATC1 = ATC2
Thus, the quantity Q at which the builder of custom motorcycles is indifferent is
Q2 – 6Q + 14 = Q2 – 10Q + 30
Q = 4
SB-
12 For Q < 4, ATC1 is less, whereas for Q > 4, ATC2 is less. Hence, the LATC is
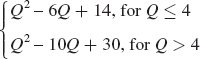
-
Suppose that a firm has the following Cobb–
Douglas production function: Q = 12K0.75 L0.25. What must its long-
run total cost curve look like? Its long- run average total cost curve? This Cobb–
Douglas production function exhibits constant returns to scale. Hence, the long- run average cost curve is horizontal, whereas the long- run total cost curve is a straight upward- sloping line. How do your answers to part (a) change if the firm’s production function is Q = KL?
Now the production function exhibits increasing returns to scale. The long-
run average cost curve is downward- sloping and the total cost curve’s slope is positive, but as output increases, the slope declines.
Peter’s Pipers produces plumbing pipe. The long-
run total cost of Peter’s pipes is LTC = 20,000Q –200Q2 + Q3, where Q is measured as thousands of feet of piping. The long- run marginal cost of Peter’s pipes is given as LMC = 20,000 – 400Q + 3Q2. Divide total cost by Q to obtain Peter’s long-
run average cost of producing pipe. Exploit the relationship between LMC and LAC to find the quantity where LAC is at a minimum.
What is the lowest possible average cost at which Peter can produce pipe?
Over what range of output does Peter’s Pipers experience economies of scale? Over what range of output does Peter’s Pipers experience diseconomies of scale?
280
In the short run, your firm can vary only the amount of labor it employs. Labor can be hired for $5 per unit, and your firm’s fixed costs are $25. Your firm’s short-
run production function is given in the table below: Labor Input Output Marginal Product of Labor Average Product of Labor Total Cost Average Total Cost Average Variable Cost Marginal Cost 1 5 2 12 3 20 4 28 5 34 6 39 7 43 8 46 9 48 Compute the marginal and average product of each worker. What shape does each take? When does the marginal product begin to fall? Average product?
Compute the total cost of producing each output level indicated in the table.
Compute the average total, average variable, and marginal cost at each level of output. When does marginal cost begin to rise? Average variable cost?
Is there a link between your answers to (a) and (c)?
 Work this problem with calculus
Work this problem with calculus