Let’s begin by solving for the profit-maximizing condition. We take the first derivative of the profit-maximization problem above with respect to quantity Q to solve for the first-order condition:

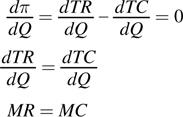
372

What does this first-order condition tell us? As we saw in the chapter, all firms—firms with some market power, monopolists, and perfectly competitive firms inclusive—produce the profit-maximizing level of output when marginal revenue equals marginal cost.

We do need to check one more condition before considering this result conclusive. Producing where MR = MC doesn’t guarantee that the firm is maximizing its profit. It only guarantees that the profit function is at one extreme or another—the firm could actually be minimizing its profit instead of maximizing it! To make sure we avoid this pitfall, we need to confirm that the second derivative of the profit function is negative:

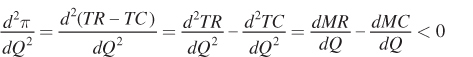
When will 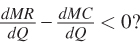This condition holds when

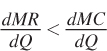
or when the change in marginal cost exceeds the change in marginal revenue. We have seen that marginal cost generally increases with output, while marginal revenue either is constant (for a price taker like the firms we saw in Chapter 8) or decreases as the quantity produced rises (for firms with market power, as we observed in Chapter 9). Therefore, this second-order condition generally is met because

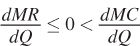
The firm has to be careful about assuming this, however. If marginal cost is declining (which can be true of a firm with increasing returns to scale over the range that it is producing), we need to confirm that marginal revenue is decreasing at a faster rate than marginal cost:

If this condition does not hold for a firm experiencing increasing returns to scale, the firm is not maximizing its profit. In this context, the firm could increase its profit by producing more output because the decrease in total cost from the additional output would be greater than the decrease in total revenue.