10.1 How People Reason I: Fast and Slow Thinking, Analogies, and Induction

To a very large extent, we reason by using our memories of previous experiences to make sense of present experiences or to plan for the future. To do so, we must perceive the similarities among various events that we have experienced. Even our most basic abilities to categorize experiences and form mental concepts depend on our ability to perceive such similarities.

When you see dark clouds gathering and hear distant thunder, you know from past experiences that rain is likely, so you take precautions against getting wet. If we were to show you a new invention that rolls along the ground on wheels, you would probably assume, from past experiences with other objects that move on wheels, that it is designed to convey things or people from place to place. Can you imagine any plan, any judgment, any thought that is not founded in some way on your ability to perceive similarities among different objects, events, or situations? Our bet is that you can’t.

Most of our everyday use of similarities to guide our thinking comes so easily and naturally that it doesn’t seem like reasoning. Sometimes our thinking is automatic—fast, seemingly effortless, and unconscious. In some cases, however, useful similarities are not so easily identified. When that happens, our thinking becomes slow, effortful, and conscious.

Fast and Slow Thinking

When we introduced the information-processing model in Chapter 9, we noted that cognitive processes could be placed on a continuum from automatic to effortful. At one extreme, automatic processes require none of the system’s limited resources; occur without intention or conscious awareness; and do not interfere with the execution of other processes, improve with practice, or vary with individual differences in intelligence, motivation, or education. At the other extreme, effortful processes are everything that automatic processes are not: They consume limited mental resources, are available to consciousness, and do interfere with the execution of other processes; they improve with practice, and they vary with individual differences in intelligence, motivation, and education. Although it is questionable whether many processes are truly fully automatic, it is useful to think of any cognitive process as falling somewhere along this continuum.

Many psychologists have proposed that, when solving problems, people have two general ways of proceeding. Such dual-processing theories typically place one way of thinking on the automatic end of the information-processing continuum, with processing being fast, automatic, and unconscious. The second way of thinking is placed on the effortful side of this continuum, with processing being slow, effortful, and conscious. Different theorists have provided different labels for the two types of thinking, including implicit/explicit, heuristic/analytic, associative/rule-based, verbatim/gist, automatic/controlled, or System 1/System 2, among others (Evans, 2010; Reber, 1989; Stanovich & West, 2000). Cognitive psychologist Daniel Kahneman, who won the Nobel Prize in Economics in 2002 for his work on human decision-making, refers to them in his 2011 book Thinking Fast and Slow as “fast” and “slow” thinking. “Fast” thinking is intuitive, with little or no sense of voluntary control. People think and remember by processing inexact, “fuzzy” memory representations rather than working logically from exact, verbatim representations (Brainerd & Reyna, 2005). In contrast, “slow” thinking involves the conscious self deciding which aspects of a problem to attend to, deciding which cognitive operations to execute, and then deliberately solving the problem.

For example, when given the over-learned problem 2 + 2 = ?, you automatically answer “4,” without thought. In fact, if you wanted to provide a wrong answer, you would first have to inhibit the correct one, the one you’ve been giving to this problem since shortly after you were out of diapers. You need a different approach to answer the problem 14 × 39 = ? You would likely immediately know that it is a multiplication problem and that you have the mental tools to solve it. You may also know that 225 and 73,936 are unlikely answers, but to get the precise answer would require a good deal of mental effort, using strategies you learned in elementary school, and maybe even a pencil and paper. The better your executive functions the sooner you would likely come up with an answer, and you would need to stop doing other tasks, such as paying attention to the television or to a conversation with a friend, while you’re computing the answer. You solved the first problem (2 + 2) using the “fast” thinking system, whereas you needed the “slow” system to solve the second problem.

In many cases, when presented with a problem, you cannot shut off the “fast” system, even if it may interfere with your arriving at the correct solution to a problem via the “slow” system. We saw this conflict in the Stroop interference effect, discussed in Chapter 9. Recall that when subjects were asked to identify the color of a printed word and ignore the color name, they took more time to answer if the word was printed in a color other than its name (for example, if the word “BLUE” was printed in red ink). Most adults cannot easily ignore the word’s meaning because their ability to read is nearly automatic (“fast”). Automatic processing of the “fast” system is also responsible for many visual illusions, such as the Müller-Lyer illusion presented in Chapter 8, in which lines of identical length appear to differ in size depending on how they are framed. One line appears longer to us (via “fast” processing), even though we know (via “slow” processing) it is not.

The “fast,” implicit system effortlessly produces impressions, feelings, and intuitions that the “slow,” explicit system considers. The effortful “slow” system thus has potential control over the “fast” system. However, when making routine decisions, the “fast” system is in control. For example, once you learn to read, drive a car, or serve a tennis ball, the deliberate, effortful system is too slow to effectively guide behavior. The “fast” system helps us read not only words but also faces (she’s angry; he’s sad), make sense of language, and make simple decisions—some of which, we will see, are in contradiction to the “correct” solutions that can only be derived by using the “slow” system.

The “fast” processing we do is similar to the type of cognition seen in preverbal infants and nonhuman animals. It is not unique to humans, although evolutionary psychologists have proposed that many of these unconscious cognitive operations may have been shaped over the course of human evolution to help us deal with recurrent problems faced by our ancestors (what to look for in a mate, for example) (Tooby & Cosmides, 2005). Although some degree of “slow,” conscious processing may be found in some nonhuman animals, no other species comes close to the effortful, explicit cognition displayed by Homo sapiens. Most of this chapter is devoted to looking at such “slow” processing, including reasoning and general intelligence. However, you should keep in mind that the second “fast” system—the one we share with other animals—is also operating and often influences how we solve everyday problems.

Analogies as Foundations for Reasoning

As William James (1890/1950) pointed out long ago, the ability to see similarities where others don’t notice them is what, more than anything else, distinguishes excellent reasoners from the rest of us. Two kinds of reasoning that depend quite explicitly on identifying similarities are analogical reasoning and, closely related to it, inductive reasoning.

In the most general sense of the term, an analogy is any perceived similarity between otherwise different objects, actions, events, or situations (Hofstadter, 2001). Psychologists, however, generally use the term more narrowly to refer to certain types of similarities and not to others. In this more restricted sense, an analogy refers to a similarity in behavior, function, or relationship between entities or situations that are in other respects, such as in their physical makeup, quite different from each other (Gentner & Kurtz, 2006).

By this more narrow and more common definition, we would not say that two baseball gloves are analogous to one another because they are too obviously similar and are even called by the same name. But we might say that a baseball glove is analogous to a butterfly net. The analogy here lies in the fact that both are used for capturing some category of objects (baseballs or butterflies) and both have a somewhat funnel-like shape that is useful for carrying out their function. If you saw some brand-new object that is easily maneuverable and has a roughly funnel-like shape, you might guess, by drawing an analogy to either a baseball glove or a butterfly net, that it is used for capturing something.

One type of analogical reasoning problem you’re likely familiar with (you find them on tests such as the SAT, GRE, and the Miller’s Analogy Test) are those that are stated A: B :: C: ?. For example, man is to woman as boy is to? The answer here, of course, is girl. One can use the knowledge of the relation between the first two elements in the problem (a man is an adult male, a woman is an adult female) to complete the analogy for a new item (boy). Analogies are thus based on similarity relations. One must understand the similarity between men and women and boys and girls if one is to solve the above analogy.

Here are two examples of the types of problems on the Miller Analogy Test, a bit more complicated than the man is to woman example:

1. PLANE is to AIR as BOAT is to (a) submarine, (b) water, (c) oxygen, (d) pilot.
2. SOON is to NEVER as NEAR is to (a) close, (b) far, (c) nowhere, (d) seldom.

Analogies are often mothers of invention The Wright brothers succeeded in developing the first functional airplane (left-hand photo) because of many analogies they perceived to both large soaring birds (such as eagles) and bicycles (they were bicycle mechanics by profession) (Johnson-Laird, 2006). Bringing together many of the attributes of birds and bikes, they built a plane that was light and highly maneuverable, had a broad wingspan, and could be easily tilted to facilitate turns and counter buffeting winds. Their competitors, who failed, had instead been focusing on building heavy planes with powerful engines, based more on analogies to automobiles than to birds and bikes.

Left: ©Bettmann/Corbis
Center: Winfried Wisniewski/The Image Bank/Getty Images
Right: Topham/The Image Works

To answer such questions correctly, you must see a relationship between the first two concepts and then apply it to form a second pair of concepts that are related to each other in the same way as the first pair. The relationship between PLANE and AIR is that the first moves through the second, so the correct pairing with BOAT is WATER. The second problem is a little more difficult. Someone might mistakenly think of SOON and NEVER as opposites and might therefore pair NEAR with its opposite, FAR. But never is not the opposite of soon; it is, instead, the negation of the entire dimension that soon lies on (the dimension of time extending from now into the future). Therefore, the correct answer is NOWHERE, which is the negation of the dimension that near lies on (the dimension of space extending outward from where you are now). If you answered the second problem correctly, you might not have consciously thought it through in terms like those we just presented; you may have just intuitively seen the correct answer. But your intuition must have been based, unconsciously if not consciously, on your deep knowledge of the concepts referred to in the problem and your understanding of the relationships among those concepts.

Figure 10.1: Sample item from Raven’s Progressive Matrices test The task is to infer the rule describing how the pattern changes within each of the first two rows and then to apply that rule to the third row to arrive at the correct solution. The solution is one of the eight choices at the bottom.

(From Raven’s Progressive Matrices (Standard Parallel, Sets A-E). Copyright © 1998 by NCS Pearson, Inc. Reproduced with permission. All rights reserved. “Raven’s Progressive Matrices and Vocabulary Scales” is a trademark, in the US and/or other countries, of Pearson Education, Inc. or its affiliates.)

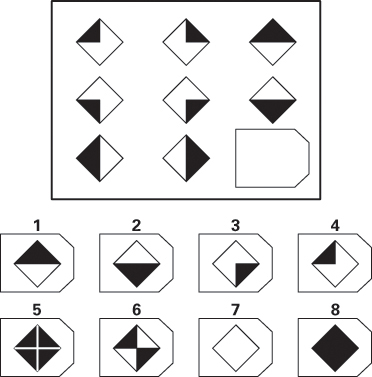
Another mental test that makes exclusive use of analogy problems is Raven’s Progressive Matrices test, which is often used by psychologists as a measure of fluid intelligence, a concept discussed later in this chapter. In this test, the items are visual patterns rather than words, so knowledge of word meanings is not essential. Figure 10.1 illustrates a sample Raven’s problem. The task is to examine the three patterns in each of the top two rows to figure out the rule that relates the first two patterns in each row to the third pattern. The rows are analogous to one another in that the same rule applies to each, even though the substance of the patterns is different from row to row. Once the rule is figured out, the problem is solved by applying that rule to the bottom row. In the example shown in Figure 10.1, the rule for each row is that the first pattern is superimposed onto the second pattern to produce the third pattern. Applying that rule to the third row shows that the correct solution to this problem, chosen from the eight pattern choices at the bottom, is number 8.

As you see, analogies can get quite complicated but, if the similarity relations are familiar to the individual, even young children can solve them. The first study to test analogical reasoning of the A: B :: C: ? type with young children was conducted by Keith Holyoak and his colleagues (1984). They gave preschool and kindergarten children some gumballs in a bowl and asked them to move the gumballs to another, out-of-reach bowl without getting out of their chairs. Available to the children were a number of objects they could use to help them solve the task including scissors, an aluminum cane, tape, string, and a sheet of paper. Before solving the problem, children heard a story about a genie with a similar problem. The genie had to move some jewels from one bottle within his reach to another bottle, out of his reach. To solve this problem the genie used his magic staff to pull the second bottle closer to him. Children were then told to think of as many ways that they could to solve their problem—to get the gumballs from one bowl to another. About half of the preschool and kindergarten children solved the problem, and the remainder did so after a hint, illustrating that these young children were capable of reasoning by analogy. However, when children were given a different analogy (the genie rolled up his magic carpet and used it as a tube to transport jewels from one bottle to another), they were much less successful. This shows that success on analogical reasoning problems is highly dependent on the similarity between objects. If someone is not familiar with one set of relations (for example, how electricity is transmitted through wires), the similarity with another relationship (for example, how nervous impulses are transmitted in the brain) will not be useful.

Use of Analogies in Scientific Reasoning

Scientists often attempt to understand and explain natural phenomena by thinking of analogies to other phenomena that are better understood. As we pointed out in Chapter 3, Charles Darwin came up with the concept of natural selection as the mechanism of evolution partly because he saw the analogy between the selective breeding of plants and animals by humans and the selective breeding that occurs in nature. Since the former type of selective breeding could modify plants and animals over generations, it made sense to Darwin that the latter type could too. Johannes Kepler developed his theory of the role of gravity in planetary motion by drawing analogies between gravity and light, both of which can act over long distances but have decreasing effects as distance becomes greater (Gentner & Markman, 1997). Neuroscientists have made progress in understanding some aspects of the brain through analogies to such human-made devices as computers.

In an analysis of discussions held at weekly laboratory meetings in many different biology labs, Kevin Dunbar (1999, 2001) discovered that biologists use analogies regularly to help them make sense of new findings and to generate new hypotheses. In a typical 1-hour meeting, scientists generated anywhere from 2 to 14 different analogies as they discussed their work. Most of the analogies were to other biological findings, but some were to phenomena completely outside the realm of biology.

Use of Analogies in Judicial and Political Reasoning and Persuasion

Lawyers, politicians, and ordinary people frequently use analogies to convince others of some claim or course of action they support. The following example is taken from a novel (Bugliosi, 1978, cited by Halpern, 1996), but it certainly could occur in real life. At the end of a trial involving much circumstantial evidence, the defense attorney, in his summation to the jury, said that evidence is like a chain: it is only as strong as its weakest link. If one piece of evidence is weak, the chain breaks and the jurors should not convict the accused. The prosecutor then stood up and told the jurors that evidence is not like a chain, but is like a rope made of many separate strands twisted together. The strength of the rope is equal to the sum of the individual strands. Even if some of the weaker strands break, the strong ones still hold the rope together. The prosecutor had the more convincing analogy and won the case.

Researchers have found that university students are good at generating analogies to defend political viewpoints. In one study, in Canada, some students were asked to defend the position that the Canadian government should eliminate deficit spending even if that would require a sharp reduction in such social programs as health care and support for the needy, and other students were asked to defend the opposite position (Blanchette & Dunbar, 2000). Students arguing on either side developed many potentially convincing analogies. Not surprisingly, many of the analogies were from the closely related realm of personal finances—comparing the national debt to one’s personal debt, or comparing a reduction in social programs to a failure to invest one’s personal money for future gain. But many other analogies were taken from more distant realms. For instance, failure to eliminate the debt was compared to failure to treat a cancer, which grows exponentially over time and becomes uncontrollable if not treated early; and failure to provide care for the needy was compared to a farmer’s failure to care for crops that have been planted, which ruins the harvest.

The next time you become involved in, or listen to, a political discussion, tune your ears to the analogies presented and, for each, ask yourself whether it helps to clarify the issue or misleads. You may be surprised at how regularly and easily analogies slip into conversations; they are a fundamental component of human thought and persuasion. We reason about new or complicated issues largely by comparing them to more familiar or less complicated issues, where the answer seems clearer. Such reasoning is useful to the degree that the structural relationships in the analogy hold true; it is misleading to the degree that those relationships don’t hold true. Good reasoners are those who are good at seeing the structural relationships between one kind of event and another.

Analogical Reasoning: “Fast” or “Slow”?

Does analogical thinking involve “fast” or “slow” thinking? Well, that depends. When the similarity relations are very familiar (such as man and woman, boy and girl), processing is fast and almost automatic. We all have detailed knowledge about these relations, and we’re ready to blurt out the answer almost before we’re certain of the question. In fact, some researchers claim that a rudimentary form of analogical reasoning is available to infants (Goswami, 1996). For example, Zhe Chen and his colleagues (1997) showed 12-month-old infants a desirable toy placed just out of their reach. Between the toy and the babies were two cloths, each with a piece of string on it, one attached to the toy and the other not. To get the toy, the infants needed to pull the cloth with the string attached to the toy and then pull the string to get the toy. Although few babies did this spontaneously on the initial problems (29 percent), most did with help from their mothers. However, the percentage of infants who successfully retrieved the toy on two subsequent trials with different toys increased to 43 percent and 67 percent, respectively. Thus, even 1-year-old infants are able to use the similarity between tasks to analogously solve problems.

Analogies are only as good as the similarity relationships on which they are based.

Scott Adams, www.dilbert.com © 2006 Distributed by United Feature Syndicate

But many analogies are not so simple, as the “SOON is to NEVER as NEAR is to _________?” example provided earlier demonstrates. In these cases, slow, effortful processing is needed to solve the problems. In fact, research has clearly shown that successful performance on challenging analogical reasoning problems is related to components of executive functions (specifically working memory and inhibition) in both adults (Cho et al., 2007) and children (Morrison et al., 2011).

Inductive Reasoning and Some Biases in It

Inductive reasoning, or induction, is the attempt to infer some new principle or proposition from observations or facts that serve as clues. Induction is also called hypothesis construction because the inferred proposition is at best an educated guess, not a logical necessity. Scientists engage in inductive reasoning all the time as they try to infer rules of nature from their observations of specific events in the world. Psychologists reason inductively when they make guesses about the workings of the human mind on the basis of observations of many instances of human behavior under varied conditions. Detectives reason inductively when they piece together bits of evidence to make inferences as to who might have committed a crime. In everyday life we all use inductive reasoning regularly to make sense of our experiences or predict new ones. When you look outside in the morning, see that the ground is wet, and say, “It probably rained last night,” you are basing that guess on inductive reasoning. Your past observations of relationships between rain and wet ground have led you to induce the general rule that wet ground usually (though not always) implies rain.

Dave Coverly

All the examples of reasoning by use of analogies, discussed earlier, are also examples of inductive reasoning. In fact, in general, inductive reasoning is reasoning that is founded on perceived analogies or other similarities. The evidence from which one induces a conclusion is, ultimately, a set of past experiences that are in some way similar to one another or to the experience one is trying to explain or predict.

Thinking Like a Scientist

Although people are exceptionally good at some forms of inductive reasoning, scientific reasoning—generating hypotheses about how something in the world works and then systematically testing those hypotheses—is a late-developing ability and something that not everyone masters. For example, Deanna Kuhn and her colleagues (1988) presented sixth- and ninth-grade students and adults with hypothetical information about the relation between certain foods and the likelihood of catching colds. The researchers first interviewed the subjects about their beliefs in which foods were associated with colds. Next, over several trials, the subjects were given a series of foods (for example, chocolate, carrots, oranges, cereal), each associated with a medical outcome (catching a cold or not). Some foods were always associated with a healthy outcome, others were always associated with catching a cold, and still others were sometimes paired with catching a cold and sometimes not. At least one food-outcome pairing was consistent with a subject’s original belief about how healthy a particular food was, and one was inconsistent with it.

Subjects’ initial responses were usually based on their prior beliefs, but as evidence accumulated most adults changed their opinions and made their judgments based on the evidence. This was less likely to happen for the adolescents. Instead, they readily agreed with the evidence when it confirmed their prior belief (chocolate has lots of sugar, which is bad for you, so it causes colds) but were reluctant to change their views when the evidence contradicted what they believed to be true (carrots are vegetables and are good for you; they don’t cause colds). However, although the adolescents and some adults were reluctant to deviate from their original opinions, most subjects were able to provide an evidenced-based answer when pressed to do so, although adolescents were still less likely to do so than adults.

Scientific reasoning can improve with practice (Kuhn et al., 2009; Schauble, 1996), and researchers have been able to train elementary school children to systematically test hypotheses (Chen & Klahr, 1999), although the long-term effects of such training for younger children (second and third graders in this study) are limited. Scientific thinking does not come easy to children (or many adults). Kuhn and her colleagues argued that one reason for this is that scientific reasoning involves a high level of metacognition—the ability to think about thinking or to reflect upon what you know. Metacognition is definitely a form of effortful, “slow” thinking and develops over childhood and differs in degree among children and adults (Schneider, 2008; Washburn et al., 2005). Kuhn (1989) proposed that scientific reasoning requires integrating theories (or hypotheses) with data (or evidence), which involves thinking about theories and not just working with them. When theory and data agree (chocolate has sugar, which is bad for you and thus may cause colds), all goes well; but when they conflict, people with poor metacognition often distort the evidence to fit the theory or simply focus on isolated patterns of results, ignoring that they may contradict their hypotheses.

Scientific reasoning notwithstanding, humans are generally very good at most forms of inductive reasoning—certainly far better than any other species of animal (Gentner, 2003). However, most psychologists who study inductive reasoning have focused not on our successes but on our mistakes, and such research has led to the identification of several systematic biases in our reasoning. Knowledge of such biases is useful to psychologists for understanding the cognitive processes that are involved in reasoning and to all of us who would like to reason more effectively.

The Availability Bias

The availability bias is perhaps the most obvious and least surprising bias in inductive reasoning. When we reason, we tend to rely too strongly on information that is readily available to us and to ignore information that is less available. When students were asked whether the letter d is more likely to occur in the first position or the third position of a word, most people said the first (Tversky & Kahneman, 1973). In reality, d is more likely to be in the third position; but, of course, people find it much harder to think of words with d in the third position than to think of words that begin with d. That is an example of the availability bias.

As another example, when asked to estimate the percentage of people who die from various causes, most people overestimate causes that have recently been emphasized in the media, such as terrorism, murders, and airplane accidents, and underestimate less-publicized but much more frequent causes, such as heart disease and traffic accidents (Brase, 2003). The heavily publicized causes are more available to conscious recall than are the less-publicized causes.

The availability bias can have serious negative consequences when it occurs in a doctor’s office. In a book on how doctors think, Jerome Groopman (2007) pointed out that many cases of misdiagnosis are the result of the availability bias. For example, a doctor who has just treated several cases of a particular disease, or for some other reason has been thinking about that disease, may be predisposed to perceive that disease in a new patient who has some of the expected symptoms. If the doctor then fails to ask the questions that would rule out other diseases that produce those same symptoms, the result may be misdiagnosis and mistreatment.

The Confirmation Bias

Textbooks on scientific method (and this book, in Chapter 2) explain that scientists should design studies aimed at disconfirming their currently held hypotheses. In principle, one can never prove absolutely that a hypothesis is correct, but one can prove absolutely that it is incorrect. The most credible hypotheses are those that survive the strongest attempts to disprove them. Nevertheless, research indicates that people’s natural tendency is to try to confirm rather than disconfirm their current hypotheses (Lewicka, 1998).

In an early demonstration of this confirmation bias, Peter Wason (1960) engaged subjects in a game in which the aim was to discover the experimenter’s rule for sequencing numbers. On the first trial the experimenter presented a sequence of three numbers, such as 6 8 10, and asked the subject to guess the rule. Then, on each subsequent trial, the subject’s task was to test the rule by proposing a new sequence of three numbers to which the experimenter would respond yes or no, depending on whether or not the sequence fit the rule. Wason found that subjects overwhelmingly chose to generate sequences consistent with, rather than inconsistent with, their current hypotheses and quickly became confident that their hypotheses were correct, even when they were not. For example, after hypothesizing that the rule was even numbers increasing by twos, a person would, on several trials, propose sequences consistent with that rule—such as 2 4 6 or 14 16 18—and, after getting a yes on each trial, announce confidently that his or her initial hypothesis was correct. Such persons never discovered that the experimenter’s actual rule was any increasing sequence of numbers.

Reasoning that matters Doctors use inductive reasoning to diagnose medical problems on the basis of evidence that they gain from interviewing patients about their symptoms. The availability bias and confirmation bias can sometimes result in false diagnoses.

Jose Luis Pelaez/Getty Images

In contrast, the few people who discovered the experimenter’s rule proposed, on at least some of their trials, sequences that contradicted their current hypothesis. A successful subject who initially guessed that the rule was even numbers increasing by twos might, for example, offer the counterexample 5 7 9. The experimenter’s yes to that would prove the initial hypothesis wrong. Then the subject might hypothesize that the rule was any sequence of numbers increasing by twos and test that with a counterexample, such as 4 7 10. Eventually, the subject might hypothesize that the rule was any increasing sequence of numbers and, after testing that with counterexamples, such as 5 6 4, and consistently eliciting no as the response, announce confidence in that hypothesis.

In other experiments demonstrating a confirmation bias, subjects were asked to interview another person to discover something about that individual’s personality (Skov & Sherman, 1986; Snyder, 1981). In a typical experiment, some were asked to assess the hypothesis that the person is an extravert (socially outgoing), and others were asked to assess the hypothesis that the person is an introvert (socially withdrawn). The main finding was that subjects usually asked questions for which a yes answer would be consistent with the hypothesis they were testing. Given the extravert hypothesis, they tended to ask such questions as “Do you like to meet new people?” And given the introvert hypothesis, they tended to ask such questions as “Are you shy about meeting new people?” This bias, coupled with the natural tendency of interviewees to respond to all such questions in the affirmative, gave most subjects confidence in the initial hypothesis, regardless of which hypothesis that was or whom they had interviewed.

Groopman (2007) points out that the confirmation bias can couple with the availability bias in producing misdiagnoses in a doctor’s office. A doctor who has jumped to a particular hypothesis as to what disease a patient has may then ask questions and look for evidence that tends to confirm that diagnosis while overlooking evidence that would tend to disconfirm it. Groopman suggests that medical training should include a course in inductive reasoning that would make new doctors aware of such biases. Awareness, he thinks, would lead to fewer diagnostic errors. A good diagnostician will test his or her initial hypothesis by searching for evidence against that hypothesis.

The Predictable-World Bias

We are so strongly predisposed to find order in our world that we are inclined to “see” or anticipate order even where it doesn’t exist. Superstitions often arise because people fail to realize that coincidences are often just coincidences. Some great event happens to a man when he is wearing his green shirt and suddenly the green shirt becomes his “lucky” shirt.

The predictable-world bias is most obvious in games of pure chance. Gamblers throwing dice or betting at roulette wheels often begin to think that they see reliable patterns in the results. This happens even to people who consciously “know” that the results are purely random. Part of the seductive force of gambling is the feeling that you can guess correctly at a better-than-chance level or that you can control the odds. In some games such a belief can lead people to perform worse than they should by chance. Here’s an example.

Imagine playing a game with a 6-sided die that has 4 red sides and 2 green sides. You are asked to guess, on each trial, whether the die will come up red or green. You will get a dollar every time you are correct. By chance, over the long run, the die is going to come up red on four-sixths, or two-thirds, of the trials and green on the remaining one-third of trials. Each throw of the die is independent of every other throw. No matter what occurred on the previous throw, or the previous 10 throws, the probability that the next throw will come up red is two chances in three. That is the nature of chance. Thus, the best strategy is to guess red on every trial. By taking that strategy you will, over the long run, win on about two-thirds of the trials. That strategy is called maximizing.

What is your lucky number? The predictable-world bias may operate consciously or unconsciously to lead gamblers, in games of pure chance, to believe that they have some control over the outcome. Some might bet their “lucky numbers,” for example, in the belief that those numbers will come up more often than other numbers. This ad exploits people’s vulnerability to a predictable-world bias by suggesting that they have a better chance of winning by “playing now” than by playing later.

Tim Boyle/Getty Images

But most people who are asked to play such a game do not maximize (Stanovich & West, 2003, 2008). Instead, they play according to a strategy referred to as matching; they vary their guesses over trials in a way that matches the probability that red and green will show. Thus, in the game just described, they guess red on roughly two-thirds of the trials and green on the other one-third. They know that, over the long run, about two-thirds of the throws will be red and one-third green, and they behave as if they can predict which ones will be red and which ones will be green. But in reality they can’t predict that, so the result is that they win less money over the long run than they would if they had simply guessed red on every trial.

Depending on how you look at it, you could say that the typical players in such a game are either too smart for their own good, or not smart enough. Rats, in analogous situations—where they are rewarded more often for pressing a red bar than for pressing a green one—quickly learn to press the red one all the time when given a choice. Presumably, their maximizing derives from the fact that they are not smart enough to figure out a pattern; they just behave in accordance with what has worked best for them. Very bright people, those with the highest IQ scores, also typically maximize in these situations, but for a different reason (Stanovich & West, 2003, 2008): They do so because they understand that there is no pattern, so the best bet always is going to be red.

The predictable-world bias is, in essence, a tendency to engage in inductive reasoning even in situations where such reasoning is pointless because the relationship in question is completely random. Not surprisingly, researchers have found that compulsive gamblers are especially prone to this bias (Toplak et al., 2007). They act as if they can beat the odds, despite all evidence to the contrary and even if they consciously know that they cannot.

Outside of gambling situations, a tendency to err on the side of believing in order rather than randomness may well be adaptive. It may prompt us to seek order and make successful predictions where order exists, and that advantage may outweigh the corresponding disadvantage of developing some superstitions or mistaken beliefs. There’s no big loss in the man’s wearing his lucky green shirt every day, as long as he takes it off to wash it now and then.