10.2 How People Reason II: Deduction and Insight

Sir Arthur Conan Doyle’s famous detective, Sherlock Holmes, is likely the king of deduction. Rather than starting with a theory, or hypothesis, which is tested and modified as a result of observations, Holmes starts with facts and only then does he logically draw inferences from his observations.

Deductive reasoning, or deduction, is the attempt to derive logically the consequences that must be true if certain premises are accepted as true. Whereas inductive reasoning is reasoned guesswork, deductive reasoning (when done correctly) is logical proof, assuming that the premises really are true. In everyday life we reason deductively to derive the logical implications of statements that we hear. If you tell me that everyone in your family is over 6 feet tall, then, assuming I believe you, I know, by deduction, that everyone in your family is also over 5 feet tall. If you studied plane geometry, then you engaged in deductive reasoning that is more complex than most everyday examples as you tried to prove or disprove various correlates based on axioms that were given to you. In fact, all of mathematics is deduction. One starts, in mathematics, with certain givens and deduces the consequences.

Table 10.1 presents deductive problems that are typical of the types of problems used by psychologists who study such reasoning. Before looking at the answers, try solving each problem. The first is a series problem, which requires you to organize items into a series on the basis of a set of comparison statements and then arrive at a conclusion that was not contained in any single statement. The second is a syllogism, which presents a major premise, or proposition, and a minor premise that you must combine mentally to see if a particular conclusion is true, false, or indeterminate (cannot be determined from the premises). Did you get the correct answer to each problem? If you did, you deduced correctly.

Table 10.1: Table 10.1
Deductive-reasoning problems

Answers:
Series problem: no.
Syllogism: yes.
(Alternative forms: indeterminate, indeterminate, no.)

The Concrete Nature of Deductive Reasoning

There was a time when many psychologists believed that deductive reasoning is fundamentally a logical process best understood in mathematical terms. For example, the highly influential Swiss developmental psychologist Jean Piaget believed that people who are roughly 13 years of age or older reason deductively by applying abstract logical principles, which can be expressed mathematically (Inhelder & Piaget, 1958). According to that view, problems are solved by a sort of mental algebra, in which the specific contents of the problem are mapped onto the xs and ys of logical equations, the equations are solved, and the answers are delivered.

Today relatively few psychologists accept the “abstract logic” or (to use Piaget’s term) “formal operational” view of deductive reasoning (Evans, 2005). One reason for rejecting that view is that study after study—with people all over the world, including highly educated people in universities—has revealed that we are much better at solving problems put to us in concrete terms than problems put to us in terms of xs and ys or other abstract symbols. Research has repeatedly shown that our natural inclination is to solve deductive problems by reflecting on our real-world knowledge, not by thinking about laws of logic. One reason Sherlock Holmes’s deductive methods were so successful was that his world knowledge was so extensive. With training, people can learn laws of logic, but even those who learn them well rarely apply them to the problems of daily life.

Deductive Problems: Logic or Content?

If people used formal logic to solve syllogisms, then it should not matter whether the statements in the problem are consistent with everyday experience, violate everyday experience, or are nonsensical. All that should matter is the formal structure of the problem. But numerous experiments show that the content does matter. Consider, for example, the following two syllogisms. In each, you are instructed to use logic alone, not your knowledge of the real world. In each, you are to assume that the first two propositions are valid, and you are to judge whether or not the conclusion follows logically from those propositions.

1. All living things need water.
   Roses need water.
   Therefore, roses are living things.
2. All insects need oxygen.
   Mice need oxygen.
   Therefore, mice are insects.

Structurally, these two problems are identical. In each case, the conclusion is not valid. It does not necessarily follow, from the first two premises of the first problem, that roses are living things, or, from the first two premises of the second problem, that mice are insects. The correct conclusion for both of these syllogisms is “indeterminate.” According to the premises, roses may be living things but they don’t have to be, and mice may be insects but they don’t have to be. The premises do not say that all things that need water are living, or that all things that need oxygen are insects.

ScienceCartoonsPlus.com

When university students were given these problems, only about 30 percent got the first problem correct, but nearly all of them got the second problem correct (Stanovich, 2003). Even though the students understood that these are logic problems, not questions about real-world facts, they apparently could not resist being influenced by their knowledge of the real world. Their knowledge that roses are living things led them to believe that the conclusion to the first problem is logically valid, and their knowledge that mice are not insects led them to believe that the conclusion to the second problem is logically not valid. When the same type of problem is put to students using nonsense terms—such as “All schniezels need quisics”—typically around 70 percent get it correct (Stanovich, 2003). In that case, the content neither helps nor hinders.

The bias to use knowledge rather than formal logic in answering deductive reasoning questions can be construed as a bias to think inductively rather than deductively. Our natural tendency is to reason by comparing the current information with our previous experience, and, outside the mathematics classroom or psychology experiment on logic, that tendency generally serves us well. Part of the skill in solving problems that contradict our knowledge gained from past experience lies in our ability or willingness to suppress that knowledge.

Another “logical” task in which prior knowledge greatly influences performance is Wason’s (1966) selection task. In the abstract version of the task, subjects are shown four cards on a table, such as the ones displayed below, and given the following rule: “If a card has a vowel on one side, then it must have an even number on the other side.”

Their task is to determine if the set of cards in front of them conforms to the rule or not. To find out, they should turn over the fewest number of cards possible to determine the truth of the rule. Try it before reading on.

This is a difficult task, with fewer than 10 percent of subjects selecting the correct cards, the “A” and the “7” (Stanovich & West, 2000). Most subjects select the “A” and the “2.” According to the rule, a card with a vowel on one side must have an even number on the other side, and the only way to test this is to turn over the “A” card. But turning over the “2” card is incorrect. The rule does not state that all cards with an even number on one side must have a vowel on the other, so knowing what’s on the other side of the “2” cannot prove or disprove the rule. The critical card here is the “7.” If there is a vowel on the other side of the “7,” the rule is violated.

The problem becomes much easier, however, when instead of numbers and letters, the problem is stated in terms of relationships people know, particularly those involving social rules—what people ought to do in certain situations. Take, for example, the following set of cards (Cosmides & Tooby, 1992):

Subjects are now asked to test the following rule: “If a person is drinking alcohol, then he or she must be at least 21 years old.” Which cards do you turn over to solve this problem? The answer will likely be obvious to you, as it is to most adults: the “Beer” and “16 years old” cards. What is on the other side of the “Coke” card is irrelevant because anyone, regardless of age, can drink Coke. The same is true for is what’s on the other side of the “25 years old” card because 25-year-olds, being more than 21 years old, can drink either Coke or beer. So by changing the abstract task to one based on familiar relationships, this very difficult problem becomes much easier.

Cosmides and Tooby (1992) proposed that it is not just familiarity that makes the “drinking problem” easy; it is also easy because it is in the form of a social contract. They propose that humans evolved to be sensitive to being cheated when dealing with others and developed “cheater detectors” that are limited to social contracts. From a similar perspective, the social-contract problems reflect deontic reasoning, which is reasoning about what one may, should, or ought to do; whereas the abstract problems reflect descriptive, or indicative reasoning, which implies only a description of “facts,” and no violation of social rules. Consistent with Cosmides and Tooby’s argument, even preschool children are able to solve simple deontic reasoning problems better than similar description problems (Cummins, 1996, 2013; Harris & Núnez, 1996).

Elements of Insight

Sometimes a problem will stymie us for hours, or days, and then suddenly, “Aha!”—we see the solution. What causes such flashes of insight? What do we do to bring them about? What might we do to achieve such insights more quickly and regularly? To address these questions, psychologists have studied people’s performance on insight problems, problems that are specially designed to be unsolvable until one looks at them in a way that is different from the usual way. Insight problems often entail a mix of inductive and deductive reasoning. Sometimes the crucial insight involves perceiving some similarity or analogy that one didn’t perceive before, and sometimes it involves a new understanding of the problem’s propositions or of the steps that could or could not lead to a solution.

Two Examples of Insight Problems

One problem that psychologists have used in insight experiments is the mutilated-checkerboard problem (Robertson, 2001). Subjects are presented with a standard checkerboard that has had two of its squares, at opposite corners of the board, removed or blocked off, as shown in Figure 10.2. They are also given 31 dominos, each of which is just the right size to fit over two adjacent squares of the checkerboard. Their task is to answer correctly the following question and to explain their answer: Is it possible or impossible to set the 31 dominos on the board in such a way that they fully cover all 62 of the remaining squares of the checkerboard?

Figure 10.2: The mutilated-checkerboard problem Is It possible to fully cover all 62 squares of this incomplete checkerboard with 31 dominos?

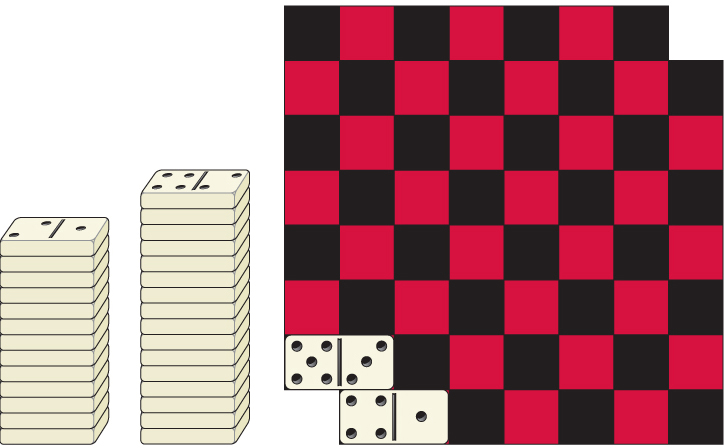
Another classic insight problem is the candle problem. Subjects are given a candle, a book of matches, and a box of tacks and are asked to attach the candle to a bulletin board in such a way that the candle can be lit and will burn properly (see Figure 10.3). They are allowed to use no objects other than those they have been given.

Figure 10.3: The candle problem Using only the objects shown here, attach the candle to the bulletin board in such a way that the candle can be lit and will burn properly.

 

Before reading the next section, spend a few minutes trying to solve each of these problems. As you work on each, pay attention to your own thought processes. If you solved either problem, how did you do it? What thoughts led you to insight? If you did not solve either problem, join the crowd. Relatively few people solve them without hints or clues of some kind. That is especially true of the mutilated-checkerboard problem. We’ll come to the solutions shortly.

Breaking Out of a Mental Set: Broadening Perception and Thought

Insight problems tend to be difficult because their solution depends on abandoning a well-established habit of perception or thought, referred to as a mental set, and then viewing the problem in a different way.

Almost everyone presented with the mutilated-checkerboard problem sees it, at first, as a problem that can be solved by trial and error (Kaplan & Simon, 1990; Robertson, 2001). By trying all possible ways of arranging the 31 dominos over the checkerboard, with each domino covering two squares, it should be possible to find out if at least one arrangement will cover all the squares. Indeed, that is a reasonable route to solving the problem—for a computer, but not for a person. Craig Kaplan and Herbert Simon (1990) wrote a computer program to solve the problem by the trial-and-error method. The program solved the problem correctly, but had to make a total of 758,148 domino placements to do so. By using mathematical means to eliminate those that are redundant with one another, it is possible to reduce the number of required domino placements to several thousand, but that is still far more than most people have time or patience for. (Some people, however, are more patient than others. Kaplan and Simon reported that a chemical engineering graduate student spent 18 hours trying to solve the problem through a combination of trial and error and mathematical formulas before giving up.)

Scott Adams copyright 1997 United Features Syndicate. Reprinted with Permission. All rights reserved.

So far, every person who has solved the mutilated-checkerboard problem and offered a convincing explanation for the solution, without writing a computer program, has done so by abandoning the trial-and-error approach. The problem is difficult partly because people fail to see that trial-and-error won’t work, so they take a long time to give up that mental set. It is not obvious to most people that to solve it that way, they would have to run through thousands of different arrangements of the dominos and keep track of all of those arrangements so as not to repeat themselves.

The candle problem is difficult because people see the objects that they are given in too narrow a way. They see the tacks and matches as potentially useful, and they try to find ways of tacking the candle to the board, or using a match to melt wax to stick the candle to the board in such a way that it tilts out from the board so it can be lit. None of those methods work. Most subjects fail to see that the box that the tacks are in could help them solve the problem. Their mental set is to see the box as just a container for the tacks, not as something that can be used to help solve the problem. Karl Duncker (1945), who invented the candle problem and performed the first experiments with it, referred to this type of mental set as functional fixedness, the failure to see an object as having a function other than its usual one. We’ll have more to say about functional fixedness later in this section.

Research in which subjects describe their thoughts aloud as they try to solve such problems shows that the first step to insight, generally, is to realize that the method they are trying is not likely to work and that a new method must be found. This realization leads people to re-examine the objects of the problem more broadly, to notice aspects of those objects that they didn’t notice before, to think more broadly about possible ways of solving the problem, and in some cases to say, “Aha!” At this point, before reading the next section, you might try again to solve the mutilated-checkerboard problem and the candle problem if you haven’t already solved them.

Discovering a Solution

Deliberate attention to aspects of the problem and materials that were not noticed before can lead to the sudden perception of a solution. Transcripts from the think-aloud study with the mutilated-checkerboard task revealed thought sequences something like the following for those who solved the problem (modified, for clarity, from Kaplan & Simon, 1990):

Figure 10.4: Variation of mutilated checkerboard The mutilated-checkerboard problem becomes easier if this bread-and-butter board is substituted for the standard checkerboard. Why?

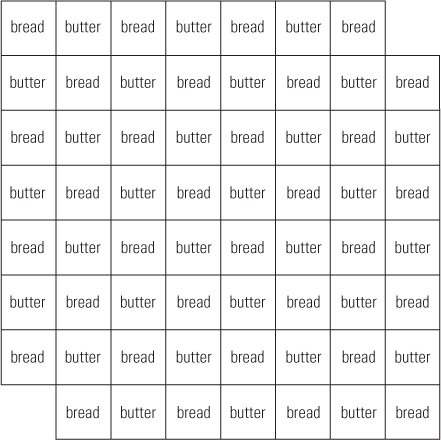
Kaplan and Simon (1990) concluded the report of their study of the mutilated-checkerboard problem by saying, “[Good problem solvers] are good noticers.” Those few who solved the problem quickly, with no or few hints, were those who noticed, early on, things about the problem to which others paid no attention. In an experiment, Kaplan and Simon (1990) showed that they could make the problem easier by making the relevant clues more obvious. Instead of using a standard checkerboard, they used, for one condition, a board in which the squares were labeled “bread” and “butter” in the alternating pattern shown in Figure 10.4. Because of the unusualness of this board, subjects paid more attention to the bread-and-butter pattern than to the black-and-red pattern on a standard board, and this led them to solve the problem more quickly. Each domino covers one bread and one butter, but there are two more breads to cover than butters, so there will always be two breads that can’t be covered.

With the candle problem, people might overcome functional fixedness by trying a different way of thinking about the problem. Instead of thinking, “How can I solve the problem with the materials I have?” they might step mentally back a bit and think, “What would I need to solve this problem?” The latter question might lead them to think, “I need something like a shelf, which can be tacked to the bulletin board.” This might then lead them to look again at the materials to see if there is anything that could serve as a shelf, and—Aha!—they see that the tack box will make an adequate shelf if the tacks are removed. They remove the tacks, tack the box to the bulletin board so it forms a shelf, melt some wax onto the shelf, and stick the candle to it. By thinking about the problem differently, they were able to see the analogy between the tack box and a shelf, and that solved the problem. Researchers have shown that the candle problem becomes easier if the tacks are placed next to the box rather than in it (Adamson, 1952). Seeing the tack box empty makes it more obvious to subjects that it could be used for something other than holding tacks.

Functional Fixedness and Tools: A Special Case?

Functional fixedness is a common phenomenon, found not just in college students in first-world countries, but also in children (German & Johnson, 2002) and people in living in traditional societies (German & Barrett, 2005). It seems to be particularly prevalent when tools are used to solve problems. Humans are not the only species to make and use tools, but no other animal makes as much use of tools, and from an early age, as Homo sapiens. Think of your day, from the time you get out of bed until you’re back in it again many hours later. How many tools did you use today? Your meals likely involved silverware, plates, or bowls. You probably used pen and paper sometime during the day, perhaps paperclips, staples, and rubber bands—all things your grandparents likely used when they were your age—and, of course, you likely used some electronics, from television and iPods to smart phones and computers. Your ancient ancestors used tools in their everyday lives as well: perhaps spears, axes, and digging sticks for hunting and gathering, as well as baskets to carry the food they foraged and slings to carry babies. What these tools, both ancient and modern, have in common is that they were all manufactured by people for a specific purpose, something that we tools users seem implicitly aware of. From an early age, people readily assume that tools are designed for an intended function, which the philosopher Daniel Dennett (1990) called the design stance. Thus, forks are for eating, axes for chopping, and objects that resemble forks and axes were likely made for eating and chopping as well.

Functional fixedness is typically seen as in a negative light, reflecting a lack of creativity and flexible thinking, and to some extend it surely is. However, given the central role of tools in human life and throughout human evolution, functional fixedness with respect to tools may be an adaptation. Once a tool has been invented and used for a specific purpose, it develops special status. It can be used for that purpose effectively without having to go through a trial-and-error process. Knowing what a tool is “for” and using it exclusively for that purpose thus provides the user increased efficiency, although at the cost of some flexibility. In the end, however, the tradeoff seems reasonable.

Figure 10.5: The light box and tools used in the study by Barrett, Davis, and Needham (2007) Twelve-and eighteen-month-old children used the novel tool to turn on the light, but displayed “functional fixedness” with the spoon, failing to use it in a novel way.

(Adapted from Barrett, T. M., David, E. F., & Needham, A. (2007). Learning about tools in infancy. Developmental Psychology, 43, 352-368. Copyright © American Psychological Association.)

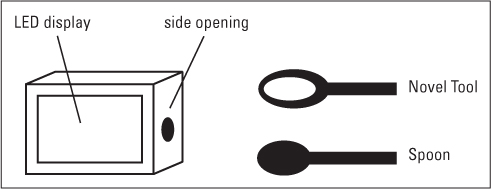
Two pieces of evidence support the contention that the design stance with respect to tools, and human artifacts in general, may be an adaptation. First, it is seen early in development. For instance, Clark Barrett and his colleagues (2007) showed 12- and 18-month-old infants a box with a light display and a small hole on its side (see Figure 10.5). The infants then watched as the experimenter grasped the round end of a spoon or of a novel spoon-like object and inserted the object’s straight end into the box, turning on the light. When infants were given an opportunity (“Now it’s your turn”) with the novel object, they grasped the round end about 60 percent of the time, successfully turning on the light. However, when they were given the spoon, fewer than 25 percent grasped the round end, failing to insert the tool into the box and turn on the light. Thus, even 1-year-olds had developed a “spoon” category, knew how a spoon should be used (hold it by the straight end), and were reluctant to use it in a nonconventional way. Other studies with 2- and 3-year-old children have found that when they are shown a function for a novel tool, they are later less apt to use it for a different task, even though it would be well suited for it—a classic demonstration of functional fixedness (Bloom & Markson, 1998; Casler & Kelemen, 2005).

The other source of evidence that the design stance with respect to tools may be an adaptation is that it is not found in other tool-using animals. For example, how chimpanzees, bonobos, gorillas (Buttelmann et al., 2007), and monkeys (Cummin-Sebree & Fragaszy, 2005) use a tool seems uninfluenced by having used the tool to solve a previous problem. They are just as likely to use a familiar tool used to solve a new problem as an equally effective novel tool. They seem to make their selection based on what will likely work, regardless of whether they have had prior experience with a tool. Thus, they behave more flexibly with respect to tools, but such flexibility likely has a cost in using a familiar tool efficiently.

Unconscious Mental Processes May Lead to Insight

A good deal of research suggests that the mental capacities required for solving insight problems are different from those required for deductive reasoning. For example, one study showed that people’s ability to solve insight problems, but not their ability to solve syllogisms, correlated positively with their creativity, measured by their ability to think of clever titles for jokes (Niu et al., 2007). Another study found that working-memory capacity, which correlates positively with the ability to solve deductive reasoning problems, did not correlate at all with the ability to achieve insight in insight problems (Ash & Wiley, 2006). Researchers have also found that people commonly solve insight problems best if they take some time off from the problem, do something else, and then come back to it (Sio & Ormerod, 2009). The time off is referred to as an incubation period. The assumption is that during incubation the person is unconsciously reorganizing the material related to the problem while consciously doing and thinking about other things. Incubation appears to facilitate insight, not deduction. Deduction requires conscious attention to the problem; it is a form of effortful, “slow” thinking.

All such observations suggest that unconscious, “fast” mental processes, which do not involve working memory, are more important for solving insight problems than for solving deductive reasoning problems. One way to think about how the brain can reach insight through unconscious means involves the notion of priming.

As discussed in Chapter 9, priming refers to the activation of a mental concept to a level that does not reach the level of consciousness, but that nevertheless makes that concept more available for forming connections to other concepts. During an incubation period, all of the elementary concepts related to an unsolved problem may remain primed, even though the person is not consciously thinking about them. As the person goes about other activities and thinks about other things, some of those primed concepts may form new associations, and, eventually, some new association may create a solution. For example, a person who has failed to solve the candle problem may, during an incubation period, come into contact with a small shelf, which may create an association to the primed concept of the tack box. Either immediately or sometime later (when the person returns to thinking about the problem), that new association may cause the solution to leap into the person’s conscious mind—“Aha! A tack box can be a shelf!”

The Value of a Happy, Playful Frame of Mind

In a classic series of experiments, Alice Isen and her colleagues showed that people are better at solving insight problems if they are made to feel happy than if they are in a serious or somber mood (Isen, 2001). In one experiment, for example, college students who had just watched a comedy film were far more successful in solving the candle problem than were those who had seen either a serious film or no film (Isen et al., 1987). In another experiment, physicians were quicker to arrive at the correct diagnosis of a liver disease, based on evidence provided by the experimenter, if they had first been given a bag of candy (Estrada et al., 1997). Those who had received the candy reasoned more flexibly, took into account all the evidence more readily, and were less likely to get stuck on false leads than those who had not received candy. Other experiments have shown that a happy mood improves people’s performance on various tests of creativity and on the ability to see whole patterns, rather than just the parts, in tests of visual perception (Fredrickson, 2003).

From the results of such research, Barbara Fredrickson (2001, 2006) developed what she called the broaden-and-build theory of positive emotions. Negative emotions, such as fear and anger, tend to narrow one’s focus of perception and thought. Those emotions lead people to focus only on the specific emotion-evoking objects and to think only of routine, well-learned ways of responding. As pointed out in Chapter 6, such narrowing may be adaptive. A moment of emergency is not the right time to test creative new ideas; it is a time for action that has proven effective in the past. In contrast, according to Fredrickson, positive emotions—such as joy and interest—broaden one’s scope of perception and thought and increase creativity. Positive emotions are felt when there is no imminent danger and one’s immediate biological needs are relatively well satisfied. That is the time to think creatively and to come up with new ideas and ways of dealing with the world. From an evolutionary perspective, the building of ideas and knowledge during periods of safety and happiness is adaptive; those ideas may prove useful in satisfying future needs or preventing future emergencies.

Our own interpretation is that it is not so much happiness per se, but the feeling of playfulness, that is conducive to learning and creativity (Gray & Chanoff, 1984). We suspect that the comedy films and bags of candy used by Isen and her colleagues put their subjects not just in a happy frame of mind, but in a playful one. Play is a time when people regularly view objects and information in new ways. In play, a tack box can easily be something other than a box for tacks. In play, one is open to considering all the information available, not just that which would seem at first glance to be most useful. A good problem solver may be one who combines the creative spirit of play with a serious search for a solution that really works.