7.2 Psychophysics

Psychophysics is the study of relationships between physical characteristics of stimuli and the sensory experiences produced by those stimuli. (You can remember the term by recalling that psychophysics relates psychological sensory experiences to physical characteristics of stimuli.) Sensory experience is typically assessed by asking subjects to make some judgment about each stimulus, such as whether it is present or absent or how it compares to another stimulus. Many experiments to be discussed later in this chapter will be psychophysical, including those assessing people’s abilities to detect or identify particular substances by taste or smell and those relating the frequency of a tone to its perceived pitch.

This section describes some psychophysical methods and findings related to (a) the detection of weak stimuli, (b) the detection of small changes in stimuli, and (c) the attempt to develop a general law relating the physical intensity of a stimulus to the intensity of the sensory experience it produces.

As you will see, psychophysics is more mathematical than most other areas of psychology. That is one of the reasons why some psychologists find it exciting. Psychophysics is the perfect cup of tea for those psychologists who like a degree of precision in their science, are drawn by the elegance of mathematics, and are fascinated by the idea that certain psychological phenomena can be described meaningfully with algebraic equations. Historically, research in psychophysics by such scientists as Ernst Weber and Gustav Fechner, in the nineteenth century, played a vital role in the founding of psychology as a science, and many of the specific questions they raised are still topics of research and debate today.

The Absolute Threshold Is a Measure of Sensitivity

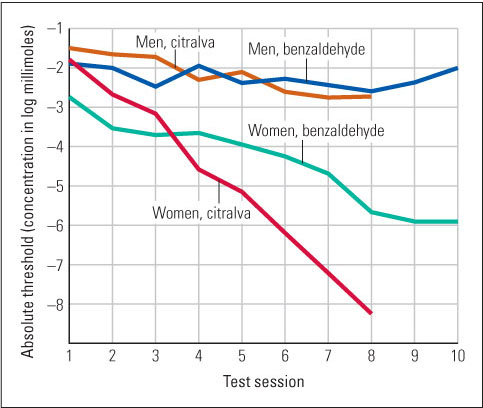
Psychophysicists refer to the faintest detectable stimulus of any given type as the absolute threshold for that type of stimulus. For example, the weakest intensity of a particular tone (say, middle C on the piano) that you can hear 50 percent of the time is your absolute threshold for that tone. The weakest solution of sodium chloride (table salt) that you can taste is your absolute threshold for sodium chloride. Absolute thresholds vary from person to person and are used clinically as measures of a person’s sensitivity to specific types of stimuli. You may well have undergone a test of your absolute threshold for various sound frequencies as a clinical test of your hearing. In general, for most senses, absolute thresholds are higher (meaning that sensitivity is lower) for older adults than for younger adults, and, for some senses, women often have greater sensitivity than men. For example, Pamela Dalton and her colleagues (2002) tested women and men repeatedly to determine their absolute thresholds for certain odorous chemicals. As shown in Figure 7.3, the women, but not the men, exhibited dramatic increases in sensitivity (declines in absolute thresholds) with repeated testing.

Figure 7.3: A sex difference in olfactory ability When women and men were tested in repeated sessions for their ability to smell weak concentrations of benzaldehyde (an almond-cherry smell) and citralva (an orange-lemon smell), the women but not the men showed dramatic improvement. By the eighth session, the women’s absolute threshold for citralva was more than five log units less than that of the men. In other words, the women were smelling this substance at concentrations less than one hundred-thousandth of the minimal concentration that the men could smell.

(Based on data from Dalton et al., 2002.)

The Difference Threshold Depends on the Magnitude of the Original Stimulus

Finding the absolute threshold In a hearing test, faint sounds of varying frequencies and amplitudes are presented to one ear at a time. To find the absolute threshold for a given frequency, for a given ear, the sound is presented at decreasing amplitudes until the person cannot detect it, and at increasing amplitudes until the person can detect it.

MR Voisin/Phanie/The Image Works

Another measure of sensitivity is the difference threshold, defined as the minimal difference in magnitude (or intensity) between two stimuli that is required for the person to detect them as different. Another name for the difference threshold is the just-noticeable difference, abbreviated jnd (by convention, small letters are used for this abbreviation).

In the early nineteenth century, the German physicist Ernst Weber (1834) conducted a systematic study of just-noticeable differences. Weber asked: What is the relationship between the jnd and the magnitude of the original stimulus? Is the jnd the same for a given type of stimulus regardless of the magnitude of the original stimulus, or does it vary in some systematic way with that magnitude?

In one series of experiments, Weber applied this question to people’s abilities to judge differences between weights. On each trial he asked the subjects to pick up each of two weights (the “original” weight and a comparison weight), one at a time, and to judge which was heavier. Weber found that the jnd varied in direct proportion to the original weight. Specifically, he found that for any original weight that he used (within a certain range), the jnd was approximately 1/30 of that weight (Gescheider, 1976). Thus, a typical subject could just barely detect the difference between a 15-gram and a 15.5-gram weight or between a 90-gram and a 93-gram weight. In the first case the jnd was 0.5 gram, and in the second it was 3 grams, but in both cases it was 1/30 of the original weight (which was always the lower of the two weights being compared).

In other experiments, Weber studied people’s abilities to discriminate between the lengths of two lines, one presented after the other, and again he found a constant proportionality between the original stimulus and the difference threshold. For this task, however, the constant fraction was 1/100 rather than 1/30. Thus, a typical subject could just barely detect the difference between a 100- and a 101-millimeter line or between a 1,000- and a 1,010-millimeter line.

On the basis of these and similar experiments, Weber formulated a general law, now called Weber’s law, stating that the jnd for stimulus magnitude is a constant proportion of the magnitude of the original stimulus. The law can be abbreviated as

in which M is the magnitude or intensity of the stimulus used as the original stimulus and k is a proportionality constant referred to as the Weber fraction, which is different for different sensory tasks (1/30 for weight judgment and 1/100 for length judgment in the examples just cited). Since Weber’s time, researchers have confirmed Weber’s law for many different types of stimuli, including sounds, sights, tastes, and smells. The law holds up rather well over a wide portion of the possible range of intensities or magnitudes for most types of stimuli, but not at the very low (near the absolute threshold) and very high ends of the range.

Sensory Magnitude Is Lawfully Related to Stimulus Magnitude

When a physical stimulus increases, our sensory experience of it also increases. When a sodium chloride solution becomes more concentrated, we taste its saltiness as stronger; when a sound increases in amplitude, we hear it as louder; when a light becomes more intense, we see it as brighter. Is it possible to specify in a mathematical equation the relationship between the magnitude of a stimulus and the magnitude of the sensory experience it produces? Such an equation was proposed by the German scientist Gustav Fechner in the middle of the nineteenth century and was tested experimentally and modified by S. S. Stevens a century later.

Fechner (1860/1966) used Weber’s law to derive a mathematical relationship between stimulus magnitude and sensory magnitude. The jnd is measured in physical units (such as grams or sound-pressure units), yet it reflects a sensory phenomenon, the just-noticeable difference between two sensations. Therefore, Fechner reasoned, the jnd could serve as a unit for relating physical and sensory magnitudes. His crucial assumptions were that (a) every jnd along a sensory dimension is equivalent to every other jnd along that dimension in the amount it adds to the sensory magnitude, and (b) jnd’s can be added together. In other words, he assumed that a sound that is 100 jnd’s above threshold would sound twice as loud as one that is 50 jnd’s above threshold, or one-tenth as loud as one that is 1,000 jnd’s above threshold.

Fechner assumed that jnd’s are subjectively equal, but he knew from Weber’s work that they are not physically equal. As you just learned, the jnd is directly proportional to the magnitude of the original stimulus. Thus, Fechner assumed that the amount of physical change needed to create a constant sensory change is directly proportional to the magnitude of the stimulus, and he showed mathematically that this can be expressed as a logarithmic relationship. (If you wish to see how he could prove this, turn to page A-9 of the Statistical Appendix at the back of the book.) Thus, Fechner derived what he believed to be a general psychophysical law, now called Fechner’s law, stating that the magnitude of the sensory experience of a stimulus is directly proportional to the logarithm of the physical magnitude of the stimulus. This law can be abbreviated as

where S is the magnitude of the sensory experience, c is a proportionality constant, and M is the magnitude of the physical stimulus.

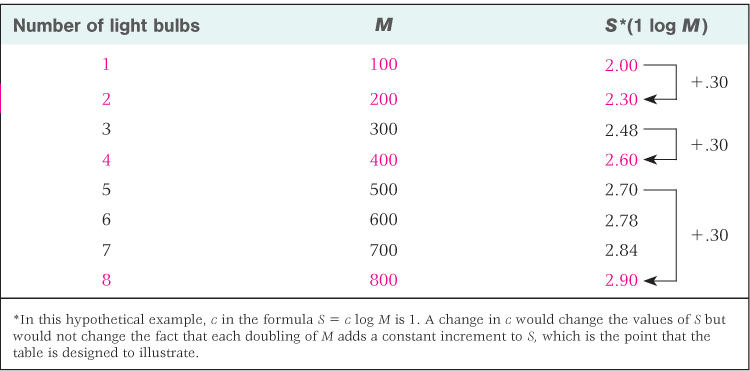
To gain a sense of the meaning of Fechner’s law, look at Table 7.2, which shows hypothetical data that are consistent with the law. Imagine a person judging the brightness of a room’s illumination with one light bulb on, then two bulbs, then three bulbs, and so on. Although each successive bulb adds a constant amount (100 units) to the physical intensity (M) of the room’s illumination, each bulb adds a progressively smaller amount to the perceived brightness (S). Thus, in the example, the second bulb adds 0.30 unit to the brightness, the third adds another 0.18 unit, the fourth adds 0.12, and so on. Notice too that every time the physical intensity (M) doubles, the sensed brightness (S) increases by a constant amount (0.30 unit in the example). Stated differently, as the physical scale increases geometrically, the sensory scale increases arithmetically. That is the essence of a logarithmic relationship. Consequently, a huge intensity range on the physical scale is condensed to a much smaller and more manageable range on the psychological scale.

Table 7.2: Table 7.2
Illustration of the relation between physical magnitude (M) and sensory magnitude (S) according to Fechner’s law

Imagine what our sensory experiences would be like if our perceptions of brightness or loudness were directly proportional to the physical intensities of lights or sounds. We would hear thunder as a thousand times louder than a normal conversation, and we would hear loud rock bands as a thousand times louder than thunder. As you’ll see when we discuss auditory perception, this is not the case (see Table 7.3, on page 270).