8.5 Seeing in Three Dimensions

One of the great early puzzles of vision, about which philosophers speculated for centuries, was that of depth perception. We automatically, effortlessly, see the world in three dimensions. Objects occupy and move in space that includes not only a vertical (up-down) and a horizontal (right-left) dimension but also a dimension of depth, or distance from our eyes. Our retinas and the images that are projected on them are two-dimensional. It is relatively easy to understand how our retinas might record the vertical and horizontal dimensions of our visual world, but how do they record the third dimension, that of depth?

A major step toward answering this question was the publication of a treatise on vision by Hermann von Helmholtz (1867/1962), the same German physiologist who developed the trichromatic theory of color vision. He argued that seeing is an active mental process. The light focused onto our retinas is not the scene we see but is simply a source of hints about the scene. Our brain infers the characteristics and positions of objects from cues in the reflected light, and those inferences are our perceptions. Helmholtz pointed out that the steps in this inferential process can be expressed mathematically, in equations relating information in the reflected light to conclusions about the positions, sizes, and shapes of objects in the visual scene. We are not conscious of these calculations and inferences; our brain works them out quickly and automatically, without our awareness.

Cues for Depth Perception

Depth perception works best when you use both eyes. You can prove that with a simple demonstration. Pick up two pencils and hold them in front of you, one in each hand, with their points toward each other. Close one eye and move the pencils toward each other to make the points touch at their tips. Chances are, you will miss by a little bit on your first attempt, and your subsequent adjustments will have something of a trial-and-error quality. Now repeat the task with both eyes open. Is it easier? Do you find that now you can see more clearly which adjustments to make to bring the points together and that you no longer need trial and error? You can see depth reasonably well with one eye alone, but you can see it better with both eyes together.

Binocular Cues for Depth

The most important binocular (two-eye) cue for depth perception is binocular disparity, which refers to the slightly different (disparate) views that the two eyes have of the same object or scene. Because the eyes are a few centimeters apart, they view any given object from slightly different angles. To see how the degree of binocular disparity varies depending on an object’s distance from your eyes, hold your index finger about a foot in front of your eyes with a wall in the background. Look at your finger with just your right eye open, then with just your left eye open, alternately back and forth. As you alternate between the two eyes, your finger appears to jump back and forth with respect to the background wall. That is because each eye views the finger from a different angle. Now move your finger farther away (out to full arm’s length), and notice that your view of it jumps a smaller distance with respect to the wall as you again alternate between right-eye and left-eye views. The farther your finger is from your eyes, the smaller is the difference in the angle between each eye and the finger; the two lines of sight become increasingly parallel.

Thus, the degree of disparity between the two eyes’ views can serve as a cue to judge an object’s distance from the eyes: The less the disparity, the greater the distance. In normal, binocular vision your brain fuses the two eyes’ views to give a perception of depth. Helmholtz (1867/1962) showed mathematically how the difference in two objects’ distance from the eyes can be calculated from differences in the degree of binocular disparity. More recently, researchers have found that neurons in an area of the visual cortex close to the primary visual area respond best to stimuli that are presented to both eyes at slightly disparate locations on the retina (Thomas et al., 2002). These neurons appear to be ideally designed to permit depth perception. For another demonstration of binocular disparity, see Figure 8.26.

Figure 8.26: Demonstration of binocular disparity The two eyes see somewhat different views of the relationship between the closer figure and the more distant figure. The disparity (degree of difference) between the two views is proportional to the distance between the two objects, and that information is used by the perceptual system to perceive the depth between them.

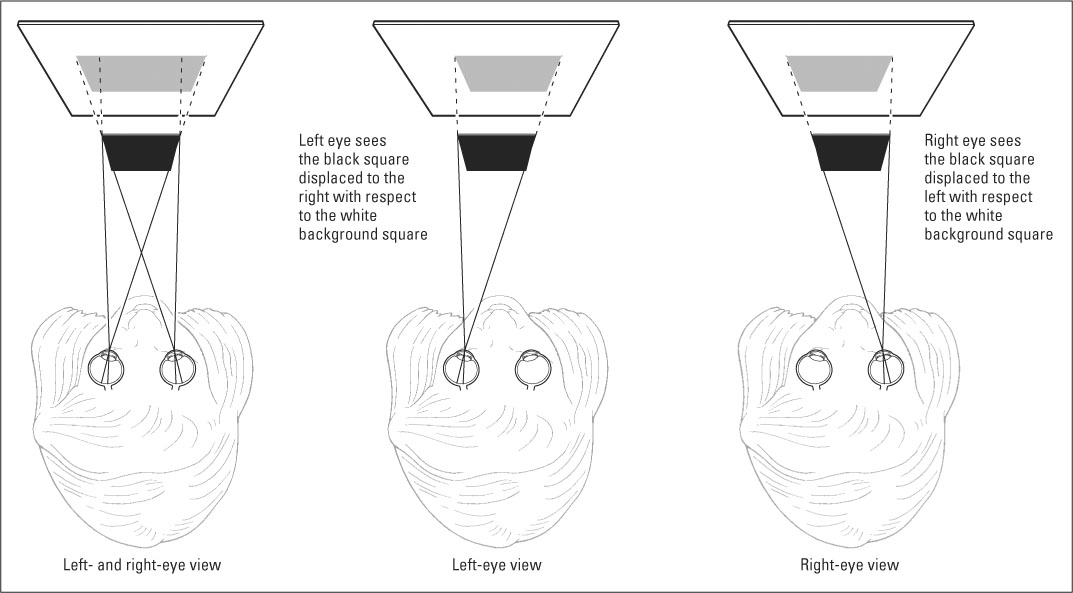
Illusions of Depth Created by Binocular Disparity

The ability to see depth from binocular disparity—an ability called stereopsis—was first demonstrated in the early nineteenth century by Charles Wheatstone (described by Helmholtz, 1867/1962). Wheatstone wondered what would happen if he drew two slightly different pictures of the same object or scene, one as seen by the left eye and one as seen by the right, and then viewed them simultaneously, each with the appropriate eye. To permit such viewing, he invented a device called a stereoscope. The effect was dramatic. When viewed through the stereoscope, the two pictures were fused perceptually into a single image containing depth.

Stereoscopes became a great fad in the late nineteenth century as they enabled people to see scenes such as Buckingham Palace or the Grand Canyon in full depth by placing cards that contained two photographs of the same scene, shot simultaneously from slightly different angles, into their stereoscope. The Viewmaster, a once-popular child’s toy, is a modern example of a stereoscope. Three-dimensional motion pictures and comic books employ the same general principle. In the simplest versions, each frame of the film or comic strip contains an overlapping pair of similar images, each in a different color, one slightly displaced from the other, and the viewer wears colored glasses that allow only one image to enter each eye. You can demonstrate stereopsis without any special viewer by looking at the two patterns in Figure 8.27 in the manner described in the caption.

Figure 8.27: A depth illusion created by binocular disparity The two patterns are constructed to appear as they would to the left and right eye, respectively, if the dark square were actually a certain distance in front of the white square (like that shown in Figure 8.26). In order to experience the three-dimensional effect, hold the book about a foot in front of your eyes and let your eyes drift in an unfocused way until you see double images of everything. You will see four renditions of the white frame with a darker square center—two renditions of (a) and two of (b). When all four of these images are clear, converge or diverge your eyes a little in order to get the right-hand image of (a) to sit right atop the left-hand image of (b). You have fused your left-eye view of (a) and your right-eye view of (b) into a single image, which now appears to be three-dimensional: The dark square seems to float in space in front of the white square.

Monocular Cues for Depth

Although depth perception is most vivid with two eyes, it is by no means absent with one. People who have just one functioning eye can drive cars, shoot basketballs, and reach out and pick objects up without fumbling around.

Motion Parallax Among the monocular (one-eye) cues for depth, perhaps the most valuable is motion parallax, which refers to the changed view one has of a scene or object when one’s head moves sideways. To demonstrate motion parallax, hold your finger up in front of your face and view it with one eye as you rock your head back and forth. As your head moves, you gain different views of the finger, and you see it being displaced back and forth with respect to the wall in the background. If you now move your finger farther away from your eye, the same head movement produces a less-changed view. Thus, the degree of change in either eye’s view at one moment compared with the next, as the head moves in space, can serve as a cue for assessing the object’s distance from the eyes: The smaller the change, the greater the distance.

As you can infer from this demonstration, motion parallax is very similar to binocular disparity. In fact, binocular disparity is sometimes called binocular parallax. The word parallax refers to the apparent change in an object or scene that occurs when it is viewed from a new vantage point. In motion parallax, the changed vantage point comes from the movement of the head, and in binocular parallax (or disparity), it comes from the separation of the two eyes.

Pictorial Cues Motion parallax depends on the geometry of true three-dimensionality and cannot be used to depict depth in two-dimensional pictures. All the remaining monocular depth cues, however, can provide a sense of depth in pictures as well as in the real three-dimensional world, and thus they are called pictorial cues for depth. You can identify some of these by examining Figure 8.28 and considering all the reasons why you see some objects in the scene as standing in the foreground and others as more distant. The pictorial cues include the following.

Figure 8.28: Pictorial cues for depth Depth cues in this picture include occlusion, relative image size for familiar objects, linear perspective, texture gradient, position relative to the horizon, and differential lighting of surfaces.

Shaun Egan/Getty Images

1. Occlusion. The trees occlude (cut off from view) part of the mountains, which indicates that the trees are closer to us than are the mountains. Near objects occlude more distant ones.
2. Relative image size for familiar objects. The image of the woman (both in the picture and on the viewer’s retina) is taller than that of the mountains. Because we know that people are not taller than mountains, we take the woman’s larger image as a sign that she must be closer to us than are the mountains.
3. Linear perspective. The rows of plants converge (come closer together) as they go from the bottom toward the mountains, indicating that objects toward the mountains are farther away. Parallel lines appear to converge as they become more distant.
4. Texture gradient. Texture elements in the picture—specifically, the individual dots of color representing the flowers—are smaller and more densely packed near the trees and mountains than they are at the bottom of the picture. In general, a gradual decrease in the size and spacing of texture elements indicates depth.
5. Position relative to the horizon. The trees are closer to the horizon than is the woman, indicating that they are farther away. In outdoor scenes, objects nearer the horizon are usually farther away than those that are displaced from the horizon in either direction (either below it or above it). If there were clouds in this picture, those seen just above the edge where the earth and sky meet (close to the horizon) would be seen as farther away than those seen farther up in the picture (farther from the horizon).
6. Differential lighting of surfaces. In real three-dimensional scenes the amount of light reflected from different surfaces varies as a function of their orientation with respect to the sun or other source of light. The fact that the sides of the rows of lavender are darker than the tops leads us to see the rows as three-dimensional rather than flat. We see the brightest parts of the plants as their tops, closest to us (as we look down on them); and we see the darker parts as their sides, shaded by the tops, and farther from us. For an even more dramatic demonstration of an effect of lighting, see Figure 8.29 and follow the directions in its caption.

Figure 8.29: Depth perception created by light and shade Because we automatically assume that the light is coming from above, we see the smaller disruptions on the surface here as bumps and the larger ones as pits. Turn the picture upside down and see what happens. (The bumps and pits reverse.)

Vilayanur S. Ramachandran & Diane Rogers-Ramachandran. Reproduced with permission. Copyright © (2004) Scientific American, Inc. All rights reserved.

The Role of Depth Cues in Size Perception

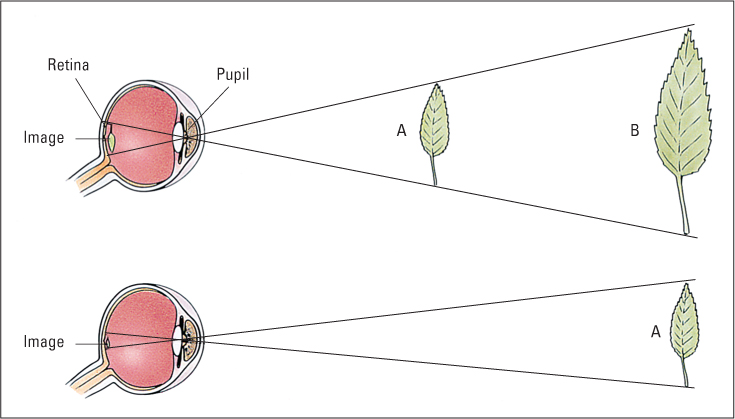
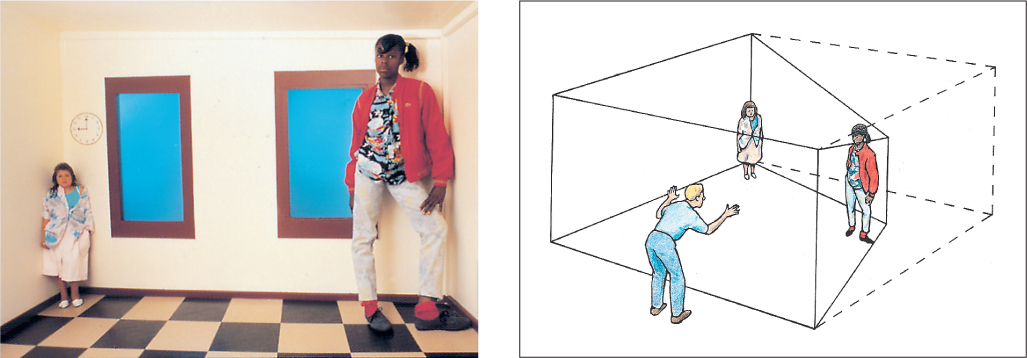
The ability to judge the size of an object is intimately tied to the ability to judge its distance. As Figure 8.30 illustrates, the size of the retinal image of an object is inversely proportional to the object’s distance from the retina. Thus, if an object is moved twice as far away, it produces a retinal image half the height and width of the one it produced before. You don’t see the object as smaller, though, just farther away. The ability to see an object as unchanged in size, despite change in the image size as it moves farther away or closer, is called size constancy. For familiar objects, such as a pencil or a car, previous knowledge of the object’s usual size may contribute to size constancy. But size constancy also occurs for unfamiliar objects if cues for distance are available, and even familiar objects can appear to be drastically altered in size if misleading distance cues are present (for an example, see Figure 8.31).

Figure 8.30: Relationship of retinal-image size to object size and distance If, as in the upper sketch, object B is twice as tall and wide as object A and also twice as far from the eye, the retinal images that the two objects produce will be the same size. If, as in the lower sketch, object A is moved twice its former distance from the eye, the retinal image produced will be half its former height and width.

Figure 8.31: A size-distance illusion We know that these young women must be approximately the same size, so what explains this illusion? The room they are standing in is distorted. The back wall and both windows are actually trapezoidal in shape, and the wall is slanted so that its lefthand edge is actually twice as tall and twice as far away from the viewer as its right-hand edge (see drawing at right). When we view this scene through a peephole (or the camera’s eye), we automatically assume that the walls and window are normal, that the occupants are the same distance away, and therefore that their size is different. This distorted room is called an Ames room, after Adelbert Ames, who built the first one.

Susan Schwartzenberg, © The Exploratorium, www.exploratorium.edu

Unconscious Depth Processing as a Basis for Size Illusions

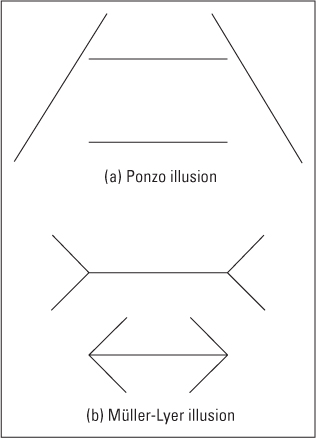
It is not difficult to produce drawings in which two identical lines or objects appear to be different in size. Two classic examples are the Ponzo illusion (first described by Mario Ponzo in 1913) and the Müller-Lyer illusion (first described by F. C. Müller-Lyer in the mid-nineteenth century), both illustrated in Figure 8.32. In each illusion two horizontal bars appear to be different in length; but if you measure them, you will discover that they are in fact identical.

Figure 8.32: The Ponzo and Müller-Lyer illusions In both (a) and (b), the top horizontal bar looks longer than the bottom one, although they are actually the same length.

Figure 8.33: Depth-processing explanation of the Ponzo illusion If this were a real, three-dimensional scene, not a photograph, and the red bars really existed as shown, the one in the background would not only look larger but would be larger than the one in the foreground.

(Adapted from Gregory, 1968.)
Sorapop Udomsri/Shutterstock

Richard Gregory (1968) offered a depth-processing theory to account for these and various other size illusions. This theory—consistent with everything said so far about the relation between size and distance—maintains that one object in each illusion appears larger than the other because of distance cues that, at some early stage of perceptual processing, lead it to be judged as farther away. If one object is judged to be farther away than the other but the two produce the same-size retinal image, then the object judged as farther away will be judged as larger. This theory applies most readily to the Ponzo illusion, in which the two converging lines provide the depth cue of linear perspective, causing (according to the theory) the upper bar to be judged as farther away, and hence larger, than the lower one. The photograph in Figure 8.33 makes this point clear.

Figure 8.34: Depth-processing explanation of the Müller-Lyer illusion Compare these sawhorses with the Müller-Lyer drawings in Figure 8.32b. If these were real sawhorses, viewed from above in the three-dimensional world, the upside-down one would be longer than the right-side-up one.

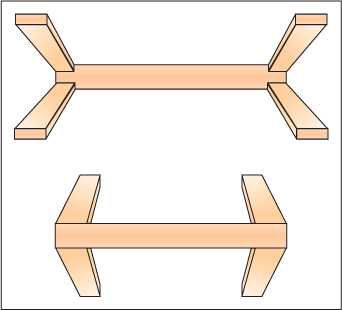
The application of the depth-processing theory to the Müller-Lyer illusion is a bit more subtle. The assumption here is that people register the figures as three-dimensional objects, something like sawhorses viewed from above. The object with wings extending outward (top drawing in Figure 8.34) resembles an upside-down sawhorse, with legs toward the viewer, and the one with inward wings (bottom drawing) resembles a right-side-up sawhorse, with its horizontal bar closer to the observer. If real sawhorses were viewed this way, the horizontal bar of the upside-down one would be farther from the observer than that of the right-side-up one, and if it produced the same-size retinal image, it would in fact be longer.

The Moon Illusion

The moon illusion has provoked debate since ancient Greek and Roman times. You have probably noticed that the moon looks huge when it is near the earth’s horizon, just above the trees or buildings in the distance, but looks much smaller when it is closer to the zenith (directly overhead). This difference is truly an illusion. Objectively, the moon is the same size, and the same distance from us, whether it is at the horizon or the zenith. If you view the horizon moon through a peephole so that you see it in isolation from other objects such as trees and buildings, the illusion disappears and the moon looks no larger than it does at the zenith.

A depth-processing account of this illusion was first proposed by the Greek astronomer Ptolemy in the second century, was revived by Helmholtz (1867/1962) in the nineteenth century, and has been supported in modern times through research conducted by Lloyd Kaufman and his colleagues (Kaufman et al., 2007; Kaufman & Rock, 1962). The account can be summarized as follows: Our visual system did not evolve to judge such huge distances as that from the earth to the moon, so we automatically assess its distance in relation to more familiar earthly objects. Most objects that we see near the earth’s horizon are farther away than objects that we see farther from the horizon (as noted earlier, in the discussion of pictorial cues for depth). For example, birds or clouds seen near the horizon are usually farther away than are those seen higher up, closer to the zenith. Thus, our perceptual system assumes that the moon is farther away at the horizon than at the zenith, even though in reality it is the same distance away from us in either position. As in the case of the Ponzo and Müller-Lyer illusions, when two objects produce the same-size retinal image and are judged to be different distances away, the one that is judged to be farther away is seen as larger than the other.

The moon illusion The moon at the horizon sometimes looks huge, much bigger than it ever looks when it is higher up in the sky. This is an unaltered photo; the moon really looked this big.

Paul Souders/The Image Bank/Getty Images

Even today, the main objection to this explanation of the moon illusion is that people do not consciously see the horizon moon as farther away than the zenith moon (Hershenson, 1989, 2003). When people see the large-appearing horizon moon and are asked whether it seems farther away or closer than usual, they usually say closer. Again, however, as with the Ponzo and Müller-Lyer illusions, Kaufman and Irving Rock (1989) contend that we must distinguish between unconscious and conscious assessments. From their perspective, the sequence of perceptual assessments about the horizon moon might be described as follows:

1. Unconscious processes judge that the moon is farther away than usual (because objects near the horizon are usually farthest away).
2. Unconscious processes judge that the moon is larger than usual (because if it is farther away but produces the same-size retinal image, it must be larger), and this judgment enters consciousness.
3. If asked to judge distance, most people say that the horizon moon looks closer (because they know that the moon doesn’t really change size, so its large apparent size must be due to closeness). This explanation has been referred to as the farther-larger-nearer theory (Ross & Plug, 2002).

Not all perceptual psychologists agree with the depth-processing account of the moon illusion, or with that of the Ponzo or Müller-Lyer illusions, but that account seems to be supported by more evidence and logic than any other explanations that have been offered to date (Hershenson, 1989; Kaufman & Kaufman, 2000; Ross & Plug, 2002).

Although perceptual psychologists have made great strides since the days of Ptolemy, we are still a long way from a full account of the calculations that our brains make to infer the sizes, distances, and shapes of all the objects in our field of view.