Chapter 1. Applying Models to Thermal Phenomena
Introduction
CONTENTS
1.1 Where we are headed in this chapter
1.2 Phenomena, Data Patterns, Questions
1.3 Three-Phase Model of Matter
1.4 Energy-Interaction Model
1.5 Examples of Particular Models
1.6 Looking Back and Ahead
In the next two chapters we will introduce and gain a lot of experience using a universally applicable model, perhaps the most powerful model in all of science. We call this model the Energy-interaction Model. It literally applies to every kind of interaction we have ever encountered, involving the smallest subatomic particles to the evolution of our entire universe from the time of the Big Bang. It can help us explain every kind of phenomena imaginable. This model incorporates the Principle of Conservation of Energy. This principle, by itself, however, is not a particularly easy tool to use. We need to turn it into a useful tool, a tool that we can reason with, that we can answer various kinds of questions with, a tool that we can readily use to construct explanations for all kinds of phenomena. That is, we need to create a model that incorporates the principle of conservation of energy in a way that we know how to apply it to particular phenomena we are interested in, that we have questions about that we want answers to. As we develop and use the energy-interaction model, we will also learn a lot about model-based reasoning along the way. If you have not read the Appendix M1-Science and the Place of Models in Science, especially the first three sections, you should do so now.
This is the first of two chapters in which the primary focus is on learning the Energy-Interaction Model and how to use it to construct particular models of various kinds of phenomena. We will encounter two other modes in these two chapters as well, the Three-Phase Model of Pure Substances and the Intro Spring-Mass Oscillator Model (that will be substantially augmented and extended in Part-2 of the course).
Watch the video below before proceeding.
1.1 Where We Are Headed in this Chapter
40
We begin Chapter 1 talking about some phenomena you already know a lot about. As we just previously said, the energy interaction model applies to every kind of phenomena and every kind of interaction, so why start with what might seem to be some pretty boring stuff you already know a lot about. Reason (1) is you do know a lot about this phenomena, so you are not hit right off the bat with stuff you don’t know anything about. Reason (2) is that there are some very interesting parts of thermal phenomena that you probably can’t make much, if any, sense of right now. That is, you can’t explain what’s going on, why it happens, or in general, say much about it at all. We will see that by applying the Energy- Interaction Model to these seemingly very strange thermal phenomena, we can make sense of them, we can explain what is going on, and we can answer all kinds of questions about the phenomena (including some seemingly hard questions on exams). To see the universal applicability of the Energy-Interaction Model, we will also apply this model to several chemical reactions.
One rather simple kind of thermal phenomena you will immediately encounter in the discussion/lab activities involves the addition or removal of energy as heat to pure substances. You have encountered this general class of phenomena (changing the temperature of a substance and/or causing it to go through a phase change) in general physical science courses as well as in your chemistry courses. So partly as review, but also as an example of how models need to be extended and modified, we introduce the Three-Phase Model of Pure Substances in this chapter.
On the next several pink-colored pages we present some of the thermal phenomena to which we will be applying our first two models: The Three-PhaseModel of Pure Substances and the Energy-Interaction Model. Often, in this section of each chapter we will also present some of the more generalized datapatterns that have evolved from many scientific studies related to the same phenomena.
In this next section, we will also present some of the kinds of questions we will want to be able to answer, the kinds of explanations we will want to construct, and the kinds of predictions we can make using the models presented in the chapter. As we do this throughout the course, we will become much more aware of the limitations on the kinds of questions and explanations that the particular models, in this case, the Energy-Interaction Model can help us with. We will begin to get a much better feeling for when we can take an energy conservationapproach, i.e., apply the Energy-Interaction Model and when we must use a different model.
Keep in mind that in Chapter 1 we deliberately restrict the range of phenomena to which we are applying the Energy-Interaction Model to mostly thermal phenomena (and a few examples of chemical reactions) and will wait until Chapter 2 to apply the Energy-Interaction Model to mechanical interactions and processes. It is easy to forget that this is the one model that can be usefully applied to essentially any interaction or process that occurs in any branch of physical and biological science.
1.2 Phenomena, Data Patterns, and Kinds of Questions and Explanations
Phenomena and Data Patterns
The principle of conservation of energy and the Energy-Interaction Model that allows us to make effective use of this principle, applies to literally every kind of interaction. Once it was realized that “heat-energy” (now called thermal energy) was not some kind of special substance, but just one of the many ways energy increased or decreased in interactions of matter, scientists began to appreciate the universality of whatever it is that we give the label “energy” to.
It isn’t easy to define energy. During an interaction or process energy decreases in some “ways” and increases in “other ways.” In this course we use the phrase “energy system” to label a “way” a physical system can “have” energy in the Energy-Interaction Model. During an interaction between one physical system and another physical system what scientists have always found, is that the energy in some energy system(s) decreases and in other(s) it increases, but the net result is that the total amount of energy in all systems remains constant.
Sometimes it was an apparent discrepancy in the energies “adding up” properly that led to the discovery of new energy systems. That is, there were ways that physical systems could have energy that were not previously known.
In a way, the idea of energy and its use as a conservation law as we and others have presented it, really does seem to be the way our universe actually works. That is, the model seems to be exactly how the universe works. And it works this way in all circumstances. It works this way for all interactions. There appear to be no exceptions. So if it works so well, why doesn’t it just answer all of our questions?
It is true that the idea of energy conservation applies to every kind of interaction imaginable. So that is not the problem. The problem comes with the kinds ofquestions it can address and the kinds of answers it can be used to develop.
Kinds of Questions
The Energy-Interaction Model, like all conservation principles, allows us to make very definite statements, predictions of all kinds of numerical parameters, and to answer all kinds of questions regarding what the possibilities are when an interaction occurs. What this kind of an approach cannot do is tell us much about the details of what happens during an interaction or process.
For example, an energy conservation approach can tell us precisely how much energy it takes to break apart some complicated molecule in order to rearrange its constituents into some desired product. But it can’t tell us how to cause the rearrangement to happen. It can’t help us with the details of knowing what kinds of catalysts we should try, for example to speed-up the process.
What scientists have been able to do, however, is to create a systematic approach to getting answers without having to know the messy details of how a process proceeds. This approach is extended in the last chapter of Part 1, which treats the models of thermodynamics. Thermodynamics can be thought of as the art of getting answers to the questions you are interested in without knowing “what you ought to know” to be able to do it. It sometimes almost seems like magic.
One way to think about the way the Energy-Interaction Model is used is that it is a “before and after” approach. We know some things before an interaction occurs and we use the model to answer questions and predict numerical values certain parameters will have after the interaction or process occurs. That is, we can know the before and we can know the after, but we cannot know much about what goes on during the process.
One way to get around this limitation is to redefine the interaction or process so that the before and the after get closer together. This often works to a large degree. And thermodynamics has all kinds of other tricks to get by the limitations of “not knowing the details.”
But if this kind of approach has limitations as we have been describing, why don’t we just develop theories and models that give us the details we want? There are several kinds of reasons. First, detailed models work only for a small range of phenomena, so you have to develop lots of different models, or at least variations of models, for each new question. Second, models that address the fine details get harder and harder to understand and use. High-speed numerical computers are helping us out a lot here. For example, there are plenty of questions that we really need precise and detailed answers to. Such as when will the next big earthquake hit Northern California? Details matter! Experts in getting really detailed information form models that make use of the tremendous computational power that is becoming ever more available are giving us some answers, and for those of us who live in Northern California, the answers are not so pleasant.
So the Energy-Interaction Model can’t do all our work for us, but it can answer “before and after” kinds of questions for essentially every interaction of matter we will encounter. This is why it is worth investing some mental energy in getting really comfortable with using this model with many types of phenomena.
Common SI Units Related to Energy
Some common energy units and conversions to SI:
- 1 kWh = 3.6 MJ
- 1 erg = 10-7 J
- 1 cal = 4.184 J
- 1 food Calorie (big “C” calorie) = 1 kcal = 4.184 kJ
- 1 ft•lb = 1.36 J
- 1 eV = 1.602 x 10-19 J
- 1 BTU = 778 ft•lb = 252 cal = 1.054 kJ
Table of Melting and Boiling Points, Heats of Melting and Vaporization, and Specific Heats of Some Common Substances (at a constant pressure of one atmosphere)
Comparison of common temperature scales
1.3 Three-Phase Model of Matter
Click here to view Summary
Construct Definitions
Pure substances
We adopt the standard chemistry definition that a substance is any material with a definite chemical composition. By “pure,” we simply mean that only one chemical substance is present in the sample.
Three phases
By three phases we mean the standard phases of solid, liquid, and gases of pure substances. We try to avoid the alternative phrase, “states of matter,” to avoid confusion with “thermodynamic state” (see Chapter 4).1
Note that we are choosing which relevant features to include in our model and which to exclude. The choices will definitely affect the level of detail we can address in our questions and discuss in our explanations. At this time, we are deliberately choosing to be more general to keep the model as simple as possible and at the same time, applicable to as wide a range of phenomena as possible.
Solid, Liquid, Gas
These common phases have the meanings you learned in physical science and introductory chemistry courses. Resistance to deformation and to changes of volume characterizes solids. Resistance to changes of volume characterizes liquids, but the container it fills determines the shape of liquids. If the container is not full, there will generally be a surface that does not touch the container.2 Gases are characterized by expanding to totally fill whatever space they occupy. Gases and liquids are frequently called fluids, because they can both flow.
Temperature
Temperature will take on a deeper and deeper meaning as we move through the models in Part 1. For this chapter, we need only the common meaning typically taught in introductory physical science courses. We do not yet invoke a particle model definition of temperature, which will be introduced in Chapter 3. At the simplest level, temperature is a measure of the hotness of something. Temperature is measured with thermometers of various types. Different temperature scales are related by universal agreement on the values on the different temperature scales of certain easily reproducible temperatures based on simple physical processes. The temperature scales commonly used in the United States are the thermodynamic or Kelvin scale, the Celsius scale and the Fahrenheit scale. By convention, temperatures on the Celsius and Fahrenheit scale are written with the “degree” symbol followed by an uppercase “C” or “F.” However, with the Kelvin scale, in which the kelvin (note the lowercase “k”) is the SI unit of temperature, a temperature value is written simply as a numeral followed by an uppercase “K,” as is standard within the SI system.
If you are not already thoroughly familiar with the SI system of units, you need to review this thoroughly. A good reference is the article from NIST located at http://physics.nist.gov/cuu/Units/introduction.html (NIST is the National Institute of Standards and Technology. Founded in 1901, NIST is a non-regulatory federal agency within the U.S. Commerce Department's Technology Administration.)
The Kelvin temperature scale (sometimes called the thermodynamic scale) has the value zero at the “absolute zero” of temperature. It should always be used when the value of the zero of temperature matters. It is also very helpful to remember that the size of the kelvin is the same as the size of the Celsius degree.
Phase change temperature and Change of Phase
Phase change temperature is the unique temperature at which a pure substance changes from one phase to another phase. These temperature values depend on the pressure, but if a value for the pressure is not specified, it is assumed to be one atmosphere. Most (but not all) substances are solids at a standard pressure of one atmosphere and at sufficiently low temperature. As energy is added as heat, the substance changes from a solid to a liquid at a specific fixed temperature that is unique to that particular substance, and then as heat is continually added, the substance eventually changes from a liquid to a gas at a higher fixed temperature. These fixed temperatures are referred to as the phase change temperatures. A few substances at a standard atmosphere do not pass through a liquid phase, but instead change directly from a solid to a gas, referred to as sublimation. Carbon dioxide is a common example of this phenomenon.
In the simplest form of the Three-Phase Model of Matter, the phase changes occur at the same temperature “on the way down” as “on the way up.” That is, the temperature of the change from liquid to solid as energy is removed is the same as the temperature of the phase change from solid to liquid as energy is added. Due to this symmetry, the liquid-solid or solid-liquid phase change temperature can be referred to as either the freezing or melting temperature. Likewise at the boiling point, the phase change temperature can be referred to as the boiling or condensation temperature. (In a discussion/lab activity, you will see that most pure substances don’t behave exactly the same way “on the way up” as “on the way down.” This seemingly strange behavior is actually rather common. In the discussion/lab activities, you will see how to extend and modify our simple Three-Phase Model of Matter to account for this more detailed behavior.
Heats of melting, vaporization, and sublimation
Chemists typically refer to the amount of energy that must be added to convert a standard amount of a pure substance from one phase to the next higher as the heat of fusion and the heat of vaporization. Physics textbooks often refer to these amounts of energy as “latent heats.” The table in the pink pages provides values of these heats for some common substances. Several useful references for this kind of data can be found at the NIST website: http://webbook.nist.gov/chemistry/ and through the UC Davis Library (or licensed site at other libraries) at the on-line Handbook of Chemistry and Physics, http://www.hbcpnetbase.com/ in Section 6: Fluid Properties: Enthalpy of Vaporization and Enthalpy of Fusion. Both boiling and melting temperatures as well as heats of vaporization and heats of fusion are given. Heats of fusion and vaporization are referred to as Enthalpies because the measurements are made at constant pressure. At constant pressure, as we will see in Chapter 4, changes in the state function enthalpy, abbreviated “ΔH,” are equal to transfers of energy as heat. These energies are frequently tabulated as the amount of energy per mass or as energy per mole of substance required to cause that amount of substance to change phase. That is, they are reported as intensive quantities. (The distinction between intensive and extensive properties is discussed more fully below in the discussion of heat capacities.) If these heats are given as energy per mass, they will have units of J/kg; if given as energy per mole, the units will be J/mol.
Thermal equilibrium
Thermal equilibrium means that the entire substance is at a single temperature. During a process, the temperature of one part of a substance or object or system can be at a different temperature than another part. When the temperature is not the same throughout the substance or object, energy will be transferred internally as heat in the direction to cause the system to come to the same temperature. An isolated system will eventually reach thermal equilibrium to as close as we wish to define it.
Mixed phase
If a substance is in thermal equilibrium and is at a phase change temperature, part of the substance can be in one phase, perhaps a liquid, and another part can be in an adjacent phase, perhaps a solid. A totally isolated substance can continue to exist in a mixed phase forever if it is at a phase change temperature.
Heat capacity
At temperatures between the phase change temperatures, when energy is added to a substance, the substance increases in temperature. The heat capacity of a substance is a measure of the amount of energy that must be added to increase the temperature of the substance a certain amount. The larger the heat capacity, the larger the amount of energy that must be added to achieve the same increase in temperature.
Heat capacity of a specific sample of matter is determined experimentally as the ratio of the amount of energy added as heat to the sample to the change in temperature of the sample. You probably recall from chemistry that there is often a subscript “p” or “v” attached to experimentally determined values of heat capacity, as in Cp and Cv. The subscript “p” means the measurement was carried out at constant pressure and the “v” means it was carried out at constant volume. (There is very little difference between Cp and Cv in the liquid phase or in the solid phase, but there is a large difference in the gas phase. We will discuss this in much more detail later in Chapter 4, and develop our model of matter to the point that it can provide a thorough understanding of the origin of the similarities and differences of observed heat capacities.)
If energy is added to a substance or object as heat and if there are no phase changes, then the energy transferred to the physical system as heat goes into changing the temperature, and the heat capacity is simply the amount of energy transferred, i.e., the heat, divided by the change in temperature:
Heat capacity is an extensive property. That is, it depends on the amount of substance: if you double the amount of substance, then the value of the heat capacity doubles.
Specific heat capacity, or simply specific heat as it is commonly called, is an intensive property. An intensive property of a substance does not depend on the amount of substance. The two most widely used intensive expressions for heat capacity are specific heat per unit mass and specific heat per mole, or molar specific heat.
The SI units of heat capacity and specific heat:
| heat capacity | J/K |
| specific heat per unit mass | J/kgK |
| molar specific heat | J/molK |
Meaning of the model Relationships
(Numbers below correspond to the numbered relationships on the fold-out Summary.)
- Pure substances exist in one of three phases, depending on the temperature:
solid, liquid, and gas. Non-pure substances, e.g., solutions and composites,
require more complex models for analysis.
The statement above is the simplest statement that can be made regarding ordinary matter at one atmosphere of pressure. It captures the behavior of the vast majority of pure substances. Mixtures or composites, which are composed of more than one kind of pure substance will often behave differently as the temperature increases, because one component can begin to change phase or even decompose chemically, before the other component reaches its first phase change temperature.
The following information in this paragraph is interesting to know, but is not important in terms of the understanding the model. The common exception to the statement that all substances exist in all three phases is CO2, which does not exist as a liquid at a pressure of one atmosphere, but does exist as a liquid at higher pressures. Solid carbon dioxide passes directly from the solid phase to the gas phase at its sublimation temperature when it is at one atmosphere of pressure. Another exception is the common isotope of the element helium, which does not exist as a solid, even if it is cooled to as close to the absolute zero of temperature as we wish to define zero. It remains a liquid, albeit, a very strange liquid, called a superfluid all the way down to zero at one atmosphere of pressure. - In order to change either the temperature or phase of a substance, energy must be added or removed. Often this energy is transferred to or from the substance as heat, Q, but can also be transferred as work, W.
The first relationship discussed above, could be simply interpreted as a very common data pattern that is observed for pure substances. The model part really comes into its own with this 2nd and the following 3rd and 4th relationships. This second relationship “establishes a reason” for why substances don’t just willy-nilly change their temperature or change their phase. Neither can happen unless energy is added or removed.
- Changes of phase (solid↔liquid and liquid↔gas or at some values of
pressure, solid↔gas (sublimation)) occur at specific temperatures, the phase
change temperatures (TMP, TBP, and TSP), which have particular values for
each pure substance. The values of these temperatures are the same “going
through” the phase change in “both directions.” Phase change temperatures
are, however, dependent on the pressure.
The amount of energy added or removed at a phase change (usually written as ΔH to signify constant pressure) is unique to each substance and has been measured for most substances.
If the substance is in thermal equilibrium (i.e., if the substance is all at the same temperature) at the phase change temperature, both phases will remain at the phase change temperature as the phase change occurs. Mixed phases can exist in thermal equilibrium only when the temperature has the value of the phase-change temperature.
There is a lot of meaning packed into the three statements of this third relationship. There is something unique about each kind of substance that determines how much energy is required to cause the substance to change phase. Also, in this simple model, the amount of change in energy is the same (except for the algebraic sign) whether you go through the phase transition by adding energy or by removing energy. Finally, there is a lot of meaning packed into the last part of the statement regarding when and under exactly what circumstances two phases can co-exist without one turning into the other. Think about your cold soft drink about half filled with ice and half filled with cola. If there is sufficient ice when the warmer cola is put in, and if the drink is in a well-insulated container, some ice does melt, but then the cola and ice seem to peacefully co-exist for quite some time. According to this relationship, this can only happen if what condition holds? Only if both phases are at the phase-change temperature. Additionally, this last part of the relationship tells us what must happen if energy is added sufficiently slowly so that the system is nearly in thermal equilibrium. What happens to the temperature when energy is slowly added to the mixed phase? The temperature remains at the phase change temperature until all of the substance has changed phase. When you seriously think about it, this is kind of weird. Normally, when we heat something, the temperature rises. But in this special case of mixed phases, the temperature does not rise. There is much predictive power in this last relationship.
- Changes of temperature of a substance occur when energy is added or
removed whenever the substance is not at a phase-change temperature.
This last relationship tells us what we are already familiar with. When you add energy, the temperature of the substance goes up. When the energy added is in the form of heat, the change in temperature, ΔT, is related to the amount of energy added by a property of the substance called heat capacity, C, that has a particular value for each substance. Heat capacities have been measured for most substances.
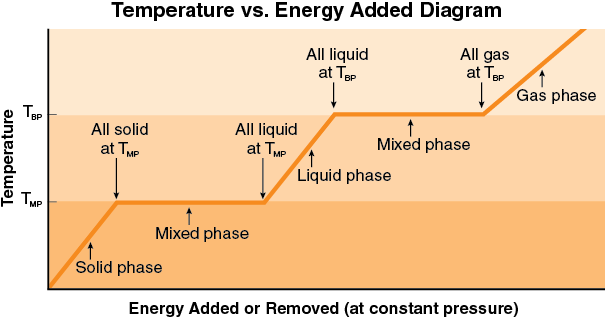
Graphical Relationship of the Three-Phase Model
The graphical representation reproduced below as well as on the blue summary sheet at the end of the resource packet, nicely summarizes all of the relationships of the model. It is very easy to be lulled into thinking this all makes sense, however, without actually digging into the meaning. You need to ask questions like, what exactly is the meaning of the horizontal portions of the graph. Can you explain in you own words “what is going on” physically in your ice cola drink during a horizontal portion of the graph? Which horizontal portion would correspond to your cold drink? What about the three slanted portions of the graph? What exactly is happening there? Where did the ice start out when you first put it into your cup? When was your drink system in thermal equilibrium, or was it ever in thermal equilibrium?
Can you picture what is happening in terms of this representation when you boil water to make tea? How is this different from putting ice trays into the freezer compartment of your refrigerator? How do the algebraic relationships relate to the graph? Which parts? What is the relationship? These are the kinds of questions you need to be asking yourself and getting confident about. You want to practice using this representation enough so that it really does become a useful tool to make sense of thermal phenomena and to be comfortable using it to construct explanations for particular phenomena.
1.4 Energy-Interaction Model (Summary on foldout #2 at back of resource packet)
Construct Definitions
Energy and energy systems
The scientific meaning of energy is rather tricky to convey in a sentence or two. There is a good reason for this: energy is an abstract concept that took scientists a long time to figure out. Although the concept of energy is truly universal in the sense that energy changes are associated with nearly all phenomena and processes, energy is not related to a single property of matter. For example, we all have an intuitive sense of “hotness” and we associate the concept of temperature with this property of matter. We associate the concept of force with the intuitive notion of push and pull. Energy, on the other hand, is associated with many properties or conditions of matter including temperature, force, motion, atomic level, mass, charge, and on and on. It is the fact that energy is so universal that makes it so difficult to define it precisely.
Another reason energy is difficult to pin down, is that the value of energy itself is seldom of importance; rather, it is the changes in the values of energy that seem to matter. In fact, we will see that change in energy is directly related to “how much” interaction occurred.
The following are useful statements about energy. Taken together they constitute a working definition of the construct (or concept of) energy. This concept will be developed further throughout the course.
- Energy is an abstract concept that characterizes the interactions of matter.
- The change in energy of a physical system is a quantifiable measure of the degree of its interactions with other physical systems.
- The importance of always being conscious of the word “change” as in the phrase “change in energy” and of the way this idea is represented mathematically cannot be overstressed. We signify “change in energy” mathematically by writing “ΔE.” The uppercase Greek symbol “Δ” often is used in science to indicate a change in some quantity. Does “ΔE” look like “E” to you? No, of course not. Yet thousands of students have seriously messed up on exam questions because they don’t seem to “see” the difference between the following two expressions:
- Historically, many “forms” or “kinds” of energy have been identified. Sometimes, the form of energy labels the interaction that resulted in a change of energy, e.g., chemical, mechanical, or nuclear. It is often misleading to think of there being different forms, kinds, or types of energy, even though we have these “names of energy” in our vocabulary. Energy is energy, regardless of how it manifests itself. Thus, instead of speaking of forms of energy or kinds of energy, we speak of energy-systems. There is usually a one-to-one correspondence between an historically identified type or form of energy and what we will identify as an energy-system.
- Energy is not a real thing that resides in systems, even though we often talk about it as if it were a “real thing.” Be careful here. Remember there is nothing at all physical about this “thing” we call energy, even when our language sometimes suggests that there is.
- Interactions are modeled by treating energy as something that resides in (can be identified with) particular energy-systems. When interactions occur, energy-systems change. Frequently, it is useful to envision energy as being transferred into and out of particular energy-systems and from one energysystem to another as interactions occur. However, it is the changes in energy systems (and not the particular transfers among energy-systems) that are the basis of the model.
Systems
We have already introduced the word “energy system.” As is frequently the case in both everyday and scientific language, the particular meaning of a word must be obtained from the context in which it is used. We will also, for example, talk about physical systems, particle systems, as well as energy systems, and doubtless a few other kinds of system, and will, like other authors, not always include the modifier, but simply refer to “the system.” Make sure you understand how the word “system” is being used in particular discussions. In general, when we say physical system it means exactly what you would think it would mean: some stuff (objects, substances, apparatus, or just a beaker of water) that we wish to focus on. The two-word phrase that we just previously introduced is the trickier one. We don’t know of a better word to use. Our language encourages us to call the “thing” we refer to as an “energy system” more than just “an energy.” But it is misleading to call it by any of the historical names that arose when scientists did not know that they were talking about the same thing. So in this course, energy system has a special meaning that will become much more clear once you start using it regularly in your discussion/lab work.
Closed and Open Physical Systems
There are two useful ways to express the principle of conservation of energy, one corresponding to closed physical systems and the other to open physical systems.
In a closed physical system, there is no transfer of energy into (or out of) that physical system from some other physical system. (This condition would generally preclude mass transfers as well, since mass transfers would also result in energy transfers.) Another way to state the condition of being closed is that all interactions occur within the one identified physical system. There are no interactions with other physical systems.
In an open physical system, there can be a net transfer of energy into (or out of) that physical system from some other physical system. Another way to state the condition of being open is that interactions can occur between matter in the identified physical system and matter in other physical systems (which might simply be the environment.
Energy Transfers: Heat, Q & Work, W
Even though energy is not a physical thing that can be transferred, it is conventional and sometimes useful to model the process as if transfers of energy actually take place among various physical systems. When energy is transferred into a physical system from another physical system, it is customary to name the energy transferred as either heat, or work. The name heat, Q, is given to energy transfers that occur as result of a difference in temperatures. Heat “flows” from the physical system at the higher temperature to the physical system at the lower temperature. (We will use the word “heat” only in this sense. Note, however, that historically, the word “heat” was also used to mean what is now more commonly called thermal energy.) The notation ΔQ will never be used, since this implies a change in a state quantity, which Q is not. However, the notation dQ will be used to mean an infinitesimally small amount of energy transferred as heat.
When you are reading science journal articles or other textbooks, especially older ones, be sure you understand how the authors are using the word “heat.” This is important, because the concept of energy transfer as heat is very different from the concept of thermal energy. We (and most modern authors) now restrict the use of the word “heat” to its meaning as a transfer of energy between physical systems as a result of temperature differences.
(The term work, W, is used to describe the energy transferred between physical systems (objects), which exert forces on one another and move relative to one another. We will examine this type of energy transfer in Chapter 2.)
One of the great advantages of an energy model is that we don’t have to be concerned with the details of how energy transfers occur. We don’t need to have a microscopic explanation, for example, of how friction causes increases in thermal energy-systems and decreases in other non-thermal energy-systems. On a microscopic scale, all kinds of energy transfers are taking place between individual atoms and molecules. The energy transfers we are talking about that occur between different physical systems are always the net transfers that occur as a result of an interaction between those physical systems.
Processes and Interactions
One of the frequent ways beginning students go astray is to not be perfectly clear in their own mind how the beginning and end of a process is defined or determined. Sometimes, we think of an interaction instead of a process. The same problem arises. What determines the beginning of the interaction and what determines the end of the interaction?
Often there is a point in time that can be identified with the beginning and the end of the interaction. This is not usually an actual clock time, such as 10 minutes after one, but rather, something happens at a particular time. The something that happens can be easily pictured in our mind and remembered. It is when the “ball was “let go” or “just before the ball hit the ground.” Or perhaps it was when the coffee pot was turned on and when the coffee pot was turned off. Something physically happens that we make a conscious decision to identify with the beginning of the time interval and something else happens that we use to identify with the end of the time interval that corresponds to the interaction or process we are interested in. It is crucial to always clearly identify these starting and ending “events,” which precisely determine the interval over which the process or interaction occurs. We often use phrases like, “Determine the interval.” to indicate precisely defining the beginning and end of a process.
State of a Physical System
Related to the discussion regarding the beginning and ending of a process or interaction is the idea also mentioned previously that we are not concerned about the details of the interaction in an energy conservation approach. In fact, all we care about is how the state of the system changed from the beginning to the end of the process or interaction. By state of the physical system we mean the values of certain parameters that changed. For the Energy-Interaction Model we care only about the indicators that tell us how much the energy changed in each energy system. This notion of state of the physical system will become more obvious as we work through more and varied phenomena using the Energy Interaction Model.
Energy Systems Related to Thermal and Chemical Processes
When dealing with thermal and chemical processes from a macroscopic perspective, it is convenient and useful to define energy systems that correspond to the empirically determined heats, i.e., the ΔH’s, that correspond to the process or interaction. These include heats associated with physical phase changes and with the formation of various molecular species. The indicator for an energy system associated with these processes would be the amount of substance that changed phase or for a chemical reaction, the amount of substance that was formed or that “disappeared.”
The general form of the expression for the amount of energy change in these processes will be
The indicator for the energy change is the amount of substance that changed, Δm. If ΔH, which is typically given as an intensive quantity, has units of J/kg, then Δm will have units of kg. If ΔH is given as a molar quantity, with units of J/mol, then Δm will have units of moles.
When there are no phase changes or chemical reactions occurring and heat is added to a substance, its temperature changes with the amount of change dependent on its heat capacity. The energy change associated with this process is exactly equal to the heat, Q, added, since we have stipulated that there are no other energy systems that are changing. From our discussion of heat capacity in the Three-Phase Model of Matter we had
Equating ΔE with Q and rearranging, we have an expression for the change in the energy system associated with this process:
Temperature is the indicator for this energy system.
These two energy systems we have just defined are very useful for two reasons. (1) They correspond to changes in indicators we can directly observe and (2) depend on parameters, (ΔH and C) that are tabulated for most substances. Additionally, as we have defined them, during a physical or chemical reaction, only one of them will be changing at a given time.
Both phase changes and chemical reactions involve the making and breaking of atomic and/or molecular bonds. When heat is added to a substance and its temperature changes, its thermal energy changes.
The two energy systems we have defined above are closely related to bond energy and thermal energy we will develop from a particle perspective in Chapter 3, but are not exactly the same. However, rather than use a different name for the energy systems involving the empirically determined parameters, ΔH and C, and macroscopic indicators, Δm and ΔT, we will simply refer to them as the bond energy system and thermal energy system, remembering that we will refine our understanding of these processes in Chapter 3 and see how the macroscopic energy systems we define here relate to the microscopically defined bond and thermal energies using particle models.
So, to summarize, our Chapter 1 and 2 understanding of the constructs bond energy system and thermal energy system is:
-
At a physical phase change, only the bond-energy system changes and the change is given by
ΔEbond = ±|Δm x (heat of the particular phase change, AH)| ,Δm is the indicator
- Between phase changes, only the thermal-energy system changes and the change is given by
ΔEthermal = C ΔT, ΔT is the indicator
- In chemical reactions, there will typically be several bond energy changes, corresponding to each of the molecular species present in either the reactants or products. The energy change for each is given by
ΔEbond = ±|Δm x (heat of formation for the particular species, ΔH)|
The temperature is assumed to have the same value after the reaction as it did before the reaction.
These energy systems, defined above, are the appropriate energy systems to use in the Energy-Interaction Model whenever we are using empirically determined values for the various ΔH’s and C’s. In the language of Appendix A1, the salient features of the phenomenon are precisely the ΔH’s and C’s characterizing the particular substance(s) and the indicators Δm and ΔT. These salient features appear in both the phenomenon and in the particular model we construct. It is this particular model that we then use to create explanations and to make numerical predictions.
It is very important to make sense of the algebraic sign of the change in the energy system based on what physically is happening. This is actually very simple to do, once you get the hang of it. However, it is easy to make a simple algebraic slip-up when actually calculating numerical values. You should always check to see if the final algebraic sign makes sense.
- Any thermal energy-system for which the temperature increases during the process will always have a positive change in energy. Likewise, any thermal energy system for which the temperature decreases will always have a negative change in energy. This is consistent with the simple notion that thermal energy increases with increases in temperature, because at higher temperatures there is “more vigorous” motion of the particles.
- Any bond energy-system for which bonds are broken during the process or interaction will always have a positive change in energy. Likewise, any bond energy-system for which bonds are formed during the process or interaction will always have a negative change in energy. This is consistent with the common experience of having to add energy (and thus increase the bond energy) to vaporize liquid water that is at 100 °C. The bonds that had existed in the liquid phase disappear (are broken) in the process of the liquid changing to a vapor. You will probably need to struggle mentally with this last point: broken bonds have more energy than intact bonds. Work on this until it “seems obvious” to you.
Commonly Used Energy Systems
| Energy system Indicator Algebraic Expression | ||
| thermal energy | temperature, t | Δ Eth = C ΔT (assuming C is constant; ΔEth will change at a phase change if C changes, but we will ignore this until we get to the model of thermodynamics) |
| bond energy (in phase changes) |
mass of a particular phase |
ΔEbond = ±|Δm Δ (heat of the particular phase change, ΔH)| (Δ m in units of kilograms or moles) |
| bond energy (in chemical reactions) |
amount of a particular molecular species |
Δebond = ±|Δm Δ (heat of formation of the particular molecular species, Δh)| (Δ m in units of moles) |
| gravitational pe | height | Δpeg = mge Δy | (positive direction of y coordinate is up) |
| translational ke |
speed |
Δke = 1/2 m Δ(v2) | |
| rotational ke |
rotational speed |
||
| elastic pe |
displacement from equilibrium |
Δpeelastic = 1/2 k Δ(x2) |
(x is measured from equilibrium position) |
| spring-mass pe |
displacement from equilibrium with mass attached |
Δpespring-mass = 1/2 k Δ(x2) | (works for both hanging and horizontal spring-mass systems. x is measured from equilibrium with mass attached ) |
Note: The mechanical energy systems listed here will be used in Chapter 2. They are listed here only for reference.
Useful Groupings of Energy Systems
| mechanical energy | sum of kinetic and potential energies associated with the physical “objects” as a whole, not with the internal energies of the objects. |
| internal energy, u | sum of kinetic and potential energies associated with the individual molecules/atoms comprising a substance, as well as the energies associated with their atomic and nuclear energies. in chapter 1 we will mostly deal only with changes in the energies associated with thermal and bond energies (chemical energies). |
Meaning of the Model Relationships
(Numbers below correspond to the numbered relationships on the fold-out Summary.)
- The heart of the Energy-Interaction Model is energy conservation, one of a small number of powerful conservation principles used throughout science. One way of expressing a conservation principle is that for an isolated physical system there are certain physical properties that do not change during an interaction or process. A process or interaction is determined by explicitly indicating the start and end points of the process or interaction; i.e., identifying the beginning and end of the interval that defines the process or interaction. The power of a conservation principle is that values of state variables (variables like P, V, T, and n for a gas) need to be known at only these two particular times (the ends of the interval), and not at intermediate times during the interval during which the process or interaction takes place. In particular, we need only know the values of the indicators of the various energy systems at the ends of the interval. It is these values that allow us to calculate actual energy changes.
- The total energy of every physical system can be expressed as a sum of the energies of separately identifiable energy systems. This division of the energy into energy systems can be carried out in multiple ways. The energy associated with a particular energy system can be expressed in terms of an observable and measurable property of the physical system. We call these properties indicators. The change in energy of each energy system can be determined from the observed change in the indicator that occurs from the beginning to the end of the time interval during which the interaction takes place.
- Conservation of energy in a closed physical system (isolated with respect to energy transfers from other physical systems):
- Conservation of energy in an open physical system:
Energy System Diagrams
Energy-system diagrams illuminate the types of energy transformations that occur when two or more physical systems interact, or when a constraint is removed and changes occur in two or more energy systems within a single physical system. The diagram helps make clear the physical systems involved, the particular energy-systems involved, and the changes in those energy-systems resulting from the interaction. The initial and final states of the systems should be clearly indicated on the diagram. These diagrams are “before-to-after” diagrams. That is, they indicate the state of the systems before the interaction occurs and the state of the systems after the interaction has occurred. (Note that there is one diagram that includes both the initial and final states. The focus is the change that occurs because of the interaction.) We use energy-system diagrams because they are useful. They help us to systematically apply the energy conservation approach to a particular physical situation using the Energy-Interaction Model.
Drawing Energy-System Diagrams When Modeling the Interaction as a CLOSED System
Listed here are the conventions we adopt in this course.
- The beginning and ending of the interaction is specified by explicitly writing down a condition of the physical system that corresponds to the beginning and end of the time interval over which the interaction occurs. These times are referred to as the initial and final times.
- The specific energy-systems that changed during the specified time interval are indicated by circles and labeled sufficiently to identify the energy-system.
- If transfers of energy to the environment are significant, due to friction, for example, include the thermal system of the environment on the energy-system diagram. That is, enlarge the boundary of the closed system to include the environment.
- The change in energy of each energy-system, whether an increase or decrease, is indicated, when known, with an “up” or “down” arrow.
- Changes in the observable parameter (indicator) associated with each energysystem that occur as a result of the interaction should be shown. If the quantitative change in the value is known, it should be given. If not, an “up” or “down” arrow can be used following the symbol of the indicator to indicate an expected increase or decrease.
Drawing Energy-System Diagrams When Modeling the Interaction as a OPEN System
Listed here are the conventions we adopt in this course.
The important difference between open and closed systems is that energy from outside the open physical system can be transferred into or out of the physical system as heat, Q, or work, W. (By definition, these transfers do not occur for a closed system.) The only difference, then, in the energy-system diagrams for the two types, is that the diagram for an open system needs to explicitly show the transfer of Q and/or W. This is done by drawing a dashed oval around all of the energy-systems (to indicate the open physical system boundary) and drawing arrows terminating on the boundary to show a Q or a W transfer.
Generic Example of an Energy System Diagram involving two physical systems, three energy systems, and with Heat Input
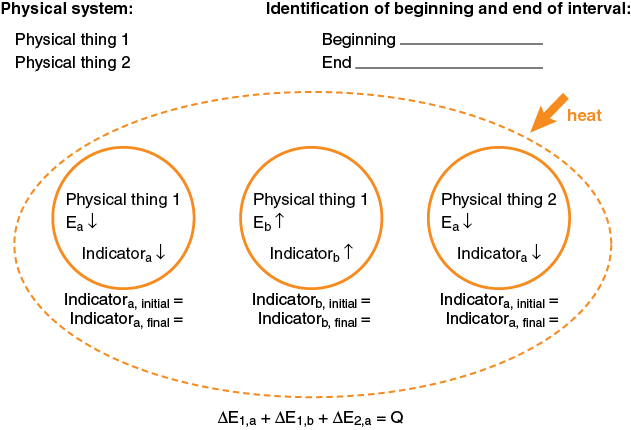
Comments:
- What is shown in the diagram above is the minimum that must always be written down. Most of the hard thinking will have been done to get to this point. Often, many explanations of physical phenomena can be constructed using this diagram without going further and substituting in explicit expressions for the individual change in energy terms and numerical values for various parameters. Even if you are required to continue the process through to a numerical result, you must do the mental work of constructing the energy-system diagram to this point prior to doing any numerical calculations.
- In an open-system diagram, the arrow showing energy transfer into the system is drawn in the direction of energy flow and labeled with the words “heat” or “work,” and not “Q” or “W.” This is to preserve the standard convention of calling Q and W positive when energy is entering the physical system. Therefore, equations expressing conservation of energy are always written as shown in the diagram, with Q and W always written on the right side of the equation (without a negative sign, even if energy is leaving the physical system). When numerical values are substituted in for Q or W, those values will be written with a negative sign, if energy is leaving the physical system.
General Process of Constructing an Energy-System Diagram
Listed here are some general questions you need to ask yourself as you use the Energy-Interaction Model. The order suggested is logical, but it is often necessaryto cycle back to previous questions. The energy-system diagram is a tool to help you use the Energy-Interaction Model. The energy-system diagram helps you keep track of the many important details you need as you construct the particular model corresponding to the particular physical situation you are interested in.
- What happened? State the essence of the physical phenomenon of interest in your own words. You don’t need to write this down, but you should have an “internal dialogue” with yourself.
- What is the boundary of the physical system you are modeling? Answer this question by listing the physical things you intend to include in the physical system. (Examples of “physical things” are: air, H2O, hand, heatpack, “all of the chemicals”.) Energy systems are always energy systems of particular physical things, so the energy systems you identify (in step (4)) will depend on the physical things you decide to include within the boundaries of your overall physical system. In some cases, it might be useful to identify two or more separate physical systems, each with its own energy-system diagram.
- What is the extent of the process or interaction? This means identifying the beginning and end of the time interval corresponding to the process/interaction that you defined and explicitly writing this on the diagram.
- What energy systems do you include in your diagram? Answer: Which indicators are changing? Each indicator that changes corresponds to an energy system that changes. Put these energy systems into your diagram as labeled circles (for example, “H2O Ethermal”). Include the indicator for each energy system inside the labeled circle with an up or down arrow showing whether the indicator increased or decreased during the process, if known. Show increases and decreases in each energy system as up or down arrows next to the abbreviation for the energy system. What you are doing here is picking out salient features from the particular instance of a physical phenomenon that relate to energy to include in the particular model you are constructing in order to answer questions, develop explanations, make numerical predictions, etc. related to the particular phenomenon you are interested in. Refer back to Appendix A1 for a general discussion of this process.
- What are the values of the indicators at the times corresponding to the ends of the time interval you chose in step (3)? Record the initial and final values of the indicators next to their respective energy systems. Remember that all of the initial and final values of indicators should correspond to the same initial and final times. (Note: It is not always necessary to identify specific initial and final values for all indicators. Sometimes, depending on the question, you only care about the change in the indicator (e.g., ΔT). At other times, you may only know that the final value of the indicator is greater than (or less than, or equal to) the initial value. The point is not to memorize a series of steps, but to be as specific as possible about what you know. The diagram is not an end in itself, but a tool to lead you through your analysis. The diagram helps you connect the particular physical phenomenon to the particular model you are constructing.)
- Is the physical system in your particular model open or closed? If you are modeling the phenomenon as an open physical system, draw a dashed oval enclosing all of the energy systems, and use an arrow that stops or starts on the oval to show heat or work entering or leaving the physical system. You may find it necessary to go back to step (2) and modify the boundary of the physical system.
- Write an equation expressing energy conservation for your particular energy system diagram, in terms of the ΔE’s. Each term in your conservation of energy equation must correspond to an energy system in your diagram.
Units for Energy
The historical development of the energy concept separately as heat and mechanical energy, as well as the widespread use of several different systems of units, has created a multitude of energy units. But, energy is energy and all forms, types, whatever, can and should be expressed in the same basic energy unit. Fortunately, this is now becoming common. The SI unit of energy is the joule, J, (rhymes with cool). All other energy units are related to the joule through an appropriate conversion factor.
A concept closely related to energy is power–the time rate of energy change or energy transfer. The SI unit of power is a joule per second and is given the name watt, W.
Fortunately, essentially everyone within the scientific and technical community has now embraced the International System (SI) system of units. We will generally use SI units in this course. However, in those instances where non-SI units are commonly used, we will use both, and expect you to be able to convert back and forth. An advantage of working exclusively in SI is that you don’t have to be concerned about unit conversions (and keeping track of them for that purpose).
SI base units
The SI base units for mass, length, and time are kilogram (kg), meter (m), and second (s). Other SI units can be expressed in base units when desired. For example, a joule is a kg m2/s2.
The kelvin (K), the SI unit for temperature, is another independent base unit. The zero of the kelvin scale is at thermodynamic zero, the so-called “absolute zero” of temperature. (Note that “kelvin” is used without the word “degree” attached.) Although the zero of the Celsius, or centigrade, scale is not at absolute zero, the kelvin is the same size as the Celsius degree. Thus, when dealing with temperature differences, it is sometimes convenient to use Celsius degrees for ΔT. For example, the SI unit for specific heat, J/kgK is equal to (and will sometimes be written as) J/kg C°.
SI Units related to energy:
Some common energy units and conversions to SI:
1 kWh = 3.6 MJ
1 erg = 10-7 J
1 cal = 4.184 J
1 food Calorie (big “C” calorie) = 1 kcal = 4.184 kJ
1 ft•lb = 1.36 J
1 eV = 1.602 x 10-19 J
1 BTU = 778 ft•lb = 252 cal = 1.054 kJ
1.5 Examples of Particular Models of Thermal Phenomena
Example 1
Let us consider the physical situation of a pot of water left on an unattended kitchen stove top. We might wish to estimate how long it would take for the 1.0 liter (1.0 kg) of water in the pan to boil away and heat the pan to dangerously high temperatures, perhaps igniting the plastic handle. Let’s also suppose we have previously determined the rate at which energy is transferred from the stove burner to the pan by doing a simple experiment to see how long it takes to heat the 1 kg of water in the pan 10°C, giving a calculated power input to the water of 1.0 kW.
In this example we are both heating the water and changing its phase; thus we know we will need to include both the thermal and bond systems of the water. How about the pan’s energy systems? If the mass of the water (1.0 kg) is several times larger than the mass of the pan (typically the case), the heat capacity of the pan will be considerably less than the water, since the mass-specific heat of the water is so much greater than steel or aluminum. What about transfer of energy to the environment from the pan? This is tougher to estimate. We do know from experience that water does boil when left on the burner for awhile. So the transfer to the environment is definitely less than from the stove to the pan. We can initially leave this out of the model and consider whether to put it in when we have made the time calculation. What about the stove energy systems? Since we know there is a heat input to the pan of 1.0 kW, it makes sense here to model the water as an open system with the heat input from “the outside.”
So at this point, our energy-system diagram would look like this:
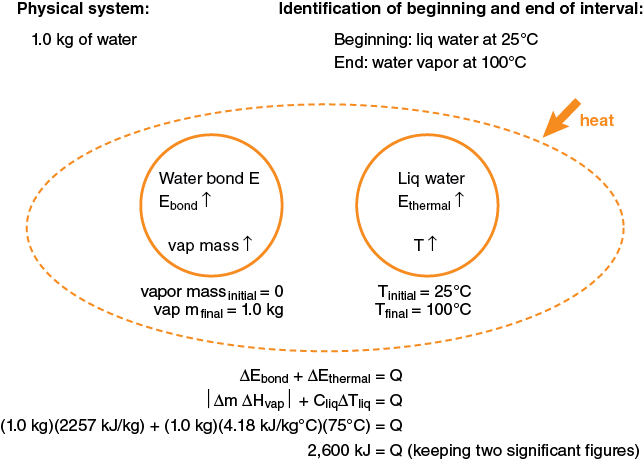
Since the heat input is 1 kW or 1 kJ/s, it would take about 2600 sec or 43 min to boil away the water.
Now we need to examine the reasonableness of our numerical predictions. First, notice that the calculated change in energy of the bond system is about seven times greater than the change in energy of the thermal system. This is at least consistent with the values of heat capacities and heats of vaporization listed in the data table. (We will develop a much deeper understanding of this difference when we further develop our particle model of matter in Chapter 3.) This difference in heats also implies that the water would come to boiling much quicker than it would take to boil it away (something like 5 minutes compared to 38 minutes). Does this correspond to your personal experience when cooking? If you haven’t noticed this considerable difference in times to heat water to boiling and to boil it away, check it out. Earlier, we raised the question weather the pan had an effect on the system. If we included the pan, what energy-system would we need to add? How would this affect our prediction of the time to boil away all of the water?
1.6 Looking Back and Ahead
Let’s reflect on what we have done in the course up to this point. Our focus has been on developing an energy model, which we’ve called the Energy-InteractionModel, and on understanding how to apply it to some particular thermal phenomena. We have used this model to begin to understand some of the more general thermal properties of matter. We will continue to develop the Energy-Interaction Model as we apply it to new kinds of phenomena in Chapter 2.
Let’s think about how we have used the Energy-Interaction Model so far. If we included all energy systems that were involved in the process or interaction, we had a closed system and modeled the physical system as being composed of several energy-systems, each of which might exchange energy with one or more of the other energy-systems within the closed system. So, to make headway with this approach, we had to be able to identify relevant energy-systems. So far, we have considered bond and thermal systems explicitly. If we thought of the physical system as being an open system, then in addition to exchanges of energy among the energy systems within the physical system, we allow for the possibility of energy entering (or leaving) the system.
The next step is to add additional energy-systems to our repertoire, so we can handle other types of phenomena with different kinds of interactions. Fortunately, there are not that many different energy-systems. So, after we have added just a few more, we will be in a position to tackle questions about many more phenomena than we could even deal with in one quarter or semester. But that is precisely the power of this approach. It is so universal that you don’t need to be shown how to use it for each different phenomenon. Once you are comfortable with the approach, it becomes your own powerful tool, which you can use anytime you need it.
What have we left out in what we have done so far? Think back over all of the phenomena we have discussed and the questions we can answer with this approach. Basically, we can get at the values of quantities, or more precisely the changes in these values that occur as a result of the interaction, but we can’t get information about the details of the interaction or what goes on during the interaction.
When we want to know something about the details of an interaction or the dynamics of the phenomenon, we will need to use an approach, or model, that incorporates these details. But precisely because we have to incorporate more detail, the models will not be nearly so general as the Energy-Interaction Model. In Part 2 of the course we will devote considerable effort to understanding the Newtonian model, which allows us to very accurately calculate motions of objects. In Part 3 we focus on a very useful wave model of motion and field models that allow us to make sense of electric and magnetic phenomena. We need these detailed models because we want to be able to answer questions that the energy-interaction model can’t help us with. But, alas, we will miss the simplicity and generality of the energy model.
Endnotes
1Although we label this model the Three Phase Model of Matter, it is strictly applicable only to pure substances. In addition, there are other phases of matter (such as magnetic phases) that are not discussed as part of this model. Many substances have several different solid phases due to different crystal structures. Some authors define a fourth phase, the plasma phase, in which at least some of the particles are ionized. In this simple model, we ignore these distinctions and focus on only the three primary phases.
2 In our simple model, we will ignore surface tension and capillarity. The effects of gravity on changes in pressure in a liquid are ignored in this simple model, but will be taken up in Part 2.